S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -755Grille de niveau 2 TDP.
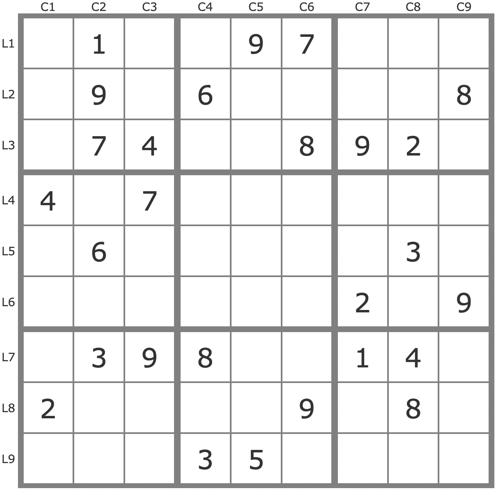
Commentaires sur cette grille
De Robert Mauriès
(Publié le 23/06/2025)
Après simplification de la grille par les TB (4 placements), un jeu de 3 pistes issues des 7L7 suffit pour résoudre la grille : P(7L7C5) couvre la grille, tandis que P(7L7C1) et P(7L7C9) sont invalides.
De Francis Labetoulle
(Publié le 23/06/2025)
Bonjour Après quelques validations, la case L7C1 est "potentiellement" l'une des plus prometteuses (nombre de dévoilés et candidats à liens forts vus). De fait : (5L7C1):0, (7L6C1):0 et (6L7C1):1. C'est très semblable à la méthode de Robert. Néanmoins: -il est possible de montrer que (5L7C1) est invalide (B8 vide de 1) et donc -5L7C1 -par suite les pistes P1(6L7C1) et P2(7L6C1) deviennent conjuguées, et se développent avec de multiples éliminations puis validations, la première P1 s'avérant la bonne, après de nombreuses validations. Voici une autre variante : P= (6L3C1) P.(5L7C1): 0. P.(7L7C1) : 0. P' : 1
De Jean
(Publié le 23/06/2025)
Bonjour, j'ai procédé comme suit : a) choix de 2 pistes pour les candidats 13 de L3C5 ; résultat : candidat 2 (commun aux deux pistes) validé en L9C9 b) choix de 2 pistes issues des candidats 13 de L3C5. La piste issue de 1 couvre la grille. Sa validation donne la solution
De Jean
(Publié le 23/06/2025)
Bonjour, j'ai procédé comme suit : a) choix de 2 pistes pour les candidats 58 de L6C7 ; résultat : candidat 2 (commun aux deux pistes) validé en L9C9 b) choix de 2 pistes issues des candidats 13 de L3C5. La piste issue de 1 couvre la grille. Sa validation donne la solution
De Philippe
(Publié le 24/06/2025)
Bonjour 4 jeu de pistes issues de paire pour venir à bout de cette grille 1 - PRouge 5L6C2 - PBleue 8L6C2 (1 élimination - validation 2L2C9) 2 - PRouge 6L9C7 - PBleue 7L9C7 (contradiction sur les bleus - validation des 5 candidats rouges) 3 - PRouge 5L6C2 - PBleue 8L6C2 (contradiction sur les bleus - validation des 20 candidats rouges) 4 - PRouge 5L1C3 - PBleue 6L1C3 (contradiction sur les rouges - les bleus couvrent la grille) Bonne journée
De François C.
(Publié le 24/06/2025)
Bonjour, Avec 4 pistes de longueur <= 10: Placement(s): 9L4C4, 9L5C1, 9L9C8, 2L4C2 Alignement: 3L4B5 => -3L6C5 -3L6C6 Alignement: 4L6B5 => -4L5C4 -4L5C5 -4L5C6 PISTE1 : 6L6C8->5L1C8->1L4C8->5L4C9->5L7C1->5L6C2->4L8C2->4L9C6->1L6C6 ->1L9C1 => 7C1 vide => -6L6C8 Alignement: 6L6B5 => -6L4C5 -6L4C6 PISTE2 : 7L5C9->4L5C7->8L4C7->7L2C8->4L1C9->1L3C9->5L3C4->2L1C4->3L3C5 ->1L4C5 => L5C4 vide => -7L5C9 Alignement: 7C9B9 => -7L8C7 -7L9C7 Placement: 6L9C7 PISTE3: 7L9C9->7L7C1->5L7C9 => 2C9 vide => -7L9C9 Placements: 2L9C9, 7L9C1, 1L6C1, 3L6C3, 8L1C1 Alignement: 3L1B3 => -3L2C7 -3L3C9 PISTE4: 6L8C3->6L3C1->3L3C5->1L9C3->8L9C2->8L6C5->1L4C5->1L2C6 => 1C8 vide => -6L8C3 Placements jusqu’à la fin.
De Robert Mauriès
(Publié le 26/06/2025)
Bonjour à tous, Cela m'a pris du temps, mais voici une résolution en 14 étapes avec des anti-pistes ne dépassant pas 7 enchaînements : (-2L9C9)->2L7C9->5L7C1->4L8C2->4L9C6->... =>-2L9C6 => L9C9=2 (-6L9C7)->7L9C7->7L7C1->5L7C9->... => -6L7C9 (-6L9C7)->7L9C7->[7L2C8->1L3C9 et 7L7C1->5L7C9]->6L4C9->... => -6L8C9 => -6L14C7 (-6L3C1)->[35L23C1 et 6L3C9->1L2C8->7L2C7->7L9C1]->6L7C1->... => -6L1C1 (-5L4C789)->5L4C6->3L4C5->1L3C5->1L2C8->7L6C8->... => -5L6C8 (-7L9C1,-8L1C1)->[7L9C7->7L5C9->4L1C9 et 8L1C3]->6L1C8->1L6C8->1L9C1->... => -8L9C1 (-6L7C56)->2L7C6->7L7C5->7L9C1->6L9C7->... => -6L9C6 (-6L3C1)->6L3C9->1L2C8->7L2C7->6L9C7->... => -6L9C1 (-8L9C2,-8L5C3)->4L9C2->1L9C6->1L8C3->5L5C3->2L5C6->6L7C6->6L9C3->... => -8L9C3 => L9C2=8 + 3 placements (-7L2C7)->7L2C8->16L6C67->1L9C1->7L9C7->... => -7L5C5 (-4L5C7)->4L5C9->7L6C8->7L2C7->... => -4L2C7 => 2 placements (-1L2C6)->1L2C8->7L2C7->7L9C1->1L6C1->... => -1L6C6 => 5 placements (-1L9C3)->6L9C3->7L9C7->7L5C9->15L5C46->... => -1L5C3 => 14 placements (-1L2C8)->1L3C9->1L5C6->... => -1L2C6 et fin Dans un premier temps, me fixant cette limite de 7 enchaînements, j'ai trouvé 20 anti-pistes répondant à ce critère avant d'atteindre la solution. Cependant 6 d'entre-elles s'avèraient inutiles.
De Cenoman
(Publié le 30/06/2025)
Ma solution en 7 pistes Piste1 : 2L9C6->4L9C2->5L8C2->5L7C9->... =>2C9 vide => -2L9C6; 1 placement Piste2 : 5L6C8->7L2C8->1L2C56->3L3C5->3L4C6->... => 5L4 vide => -5L6C8 Piste3 : 1L5C3->1L9C1->7L9C7->7L5C9->4L1C9->35L2C17->5L13C4 Et 2L2C3->2L1C4->L5C4 vide => -1L5C3; TB Piste4 : 6L6C8->5L1C8->1L4C8->5L4C9->5L7C1->5L6C2->4L8C2->4L9C6->1L6C6->1L9C1->7C1 vide => -6L6C8; 7 placements & TB Piste5 : 4L6C5->4L2C6->5L456C6->... => L6C4 vide => -4L6C5 Piste6 : 6L6C5->6L8C3->1L9C3->8L9C2->... =>8L6 vide => -6L6C5; 18 placements Piste7 : 1L3C9->1L2C6->... => 1L5 vide => -1L3C9; placements jusqu'à la fin ... et les chaînes et réseau de logiques multiples dont mes pistes sont issues (par traduction) 1. (4)L9C6 = L9C2 - (4=5)L8C2 - L7C1 = (5-2)L7C9 = (2)L9C9 => -2L9C6; 2. (7)L6C8 = (7-1)L2C8 = L2C56 - (1=3)L3C5 - L4C5 = (3-5)L4C6 = (5)L4C789 =>-5L6C8 3. Double quaternaires en réseau 3a. Quaternaire (1257)L5C4 (1)L5C4 (2)L5C4 - L1C4 = L1C3 - (2=53)L2C13 - (3|5)L2C7 (5)L5C4 - L13C4 = (53)L2C16 - (3|5)L2C7 (7)L5C4 - L5C79 = L6C8 - L2C8 = (7)L2C7 - (3|5)L2C7 => '(3|5)L2C7 => (1)L5C4' 3b. Quaternaire (3457)L2C7 (3|5)L2C7 => (1)L5C4 (4)L2C7 -L1C9 = (4-7)L5C9 = L78C9 - L9C7 = (7-1)L9C1 = (1)L6C1 (7)L2C7 - L9C7 = (7-1)L9C1 = (1)L6C1 => -1L5C3 4. Ternaire et quaternaire en réseau 4a. Quaternaire (1456)L6C6 (1)L6C6 - L6C1 = (1-7)L9C1 = (7)L7C1 - (5)L7C1 (4)L6C6 - L9C6 = L9C2 - (4=5)L8C2 - (5)L7C1 (5)L6C6 - L6C2 = (5)L8C2 - (5)L7C1 (6)L6C6 => '(5)L7C1 => (6)L6C6' 4b. Ternaire (156)L4C9 (1)L4C9 - (1=56)L14C8 (5)L4C9 - L7C9 = L7C1 => (6)L6C6 (6)L4C9 => -6L6C8 5. (4)L2C5 = (4-5)L2C6 = L456C6 - (5=4)L6C4 => -4L6C5 6. (6)L8C5 = (61-8)L89C3 = L9C2 - L6C2 = (8)L6C5 => -6L6C5 7. 1L2C8=1L2C6-1L5C6=1L5C9 =>-1L3C9-1L4C8; placements jusqu'à la fin
De Francis Labetoulle
(Publié le 01/07/2025)
Merci à tous pour les approches par antipistes de faible longueur. Je me suis "attaqué" au mémento-marquage indiqué par Bernard Cenoman. Il faut que je dépasse la méthode "papier" un peu rébarbative; je ne désespère pas d'y parvenir. Bon été... un peu moins chaud!
Ajouter un commentaire
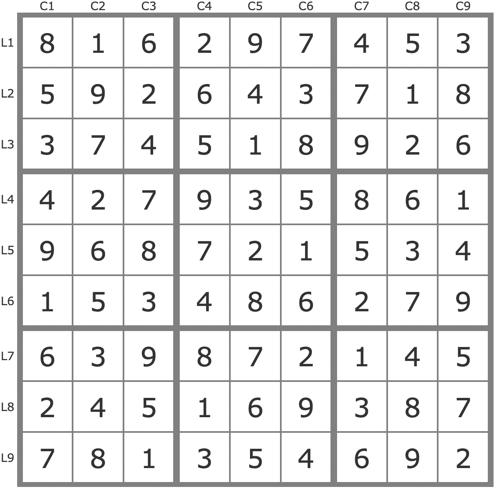
La solution
Après simplification de la grille par les TB (4 placements), un jeu de 3 pistes issues des 7L7 suffit pour résoudre la grille :
P(7L7C5) couvre la grille, tandis que P(7L7C1) et P(7L7C9) sont invalides.
Mais il est possible aussi de résoudre en plusieurs étapes avec des pistes ou des anti-pistes de longueurs limitée (Voir forum).
Voici une résolution en 14 étapes avec des anti-pistes ne dépassant pas 7 enchainements :
(-2L9C9)->2L7C9->5L7C1->4L8C2->4L9C6->... =>-2L9C7 => L9C9=2
(-6L9C7)->7L9C7->7L7C1->5L7C9->... => -6L7C9
(-6L9C7)->7L9C7->[7L2C8->1L3C9 et 7L7C1->5L7C9]->6L4C9->... => -6L8C9 => -6L14C7
(-6L3C1)->[35L23C1 et 6L3C9->1L2C8->7L2C7->7L9C1]->6L7C1->... => -6L1C1
(-5L4C789)->5L4C6->3L4C5->1L3C5->1L2C8->7L6C8->... => -5L6C8
(-7L9C1,-8L1C1)->[7L9C7->7L5C9->4L1C9 et 8L1C3]->6L1C8->1L6C8->1L9C1->... => -8L9C1
(-6L7C56)->2L7C6->7L7C5->7L9C1->6L9C7->... => -6L9C6
(-6L3C1)->6L3C9->1L2C8->7L2C7->6L9C7->... => -6L9C1
(-8L9C2,-8L5C3)->4L9C2->1L9C6->1L8C3->5L5C3->2L5C6->6L7C6->6L9C3->... => -8L9C3 => L9C2=8 + 3 placements
(-7L2C7)->7L2C8->16L6C67->1L9C1->7L9C7->... => -7L5C5
(-4L5C7)->4L5C9->7L6C8->7L2C7->... => -4L2C7 => 2 placements
(-1L2C6)->1L2C8->7L2C7->7L9C1->1L6C1->... => -1L6C6 => 5 placements
(-1L9C3)->6L9C3->7L9C7->7L5C9->15L5C46->... => -1L5C3 => 14 placements
(-1L2C8)->1L3C9->1L5C6->... => -1L2C6 et fin
 En savoir plus ...
En savoir plus ...




