L'assistant sudoku
L'assistant sudoku vous aide à résoudre vos grilles sudoku les plus difficiles. L'assistant sudoku ne recherche pas la solution à votre place, il vous aide seulement à résoudre votre grille.En savoir plus ...
Une technique universelle de résolution
La technique des pistes permet de résoudre les grilles les plus difficiles. Cette technique intuitive évite de mémoriser les nombreuses méthodes dites "Expertes" utilisées habituellement.Tous les détails de la technique sont exposés dans le livre de R. Mauriès.
En savoir plus ...
Résolution guidée
Régulièrement ici une nouvelle grille et sa résolution par la technique des pistes.Toutes les grilles avec résolution guidée
Grille -490 (Publiée le 25/04/2018)
Grille de niveau 2 TDP.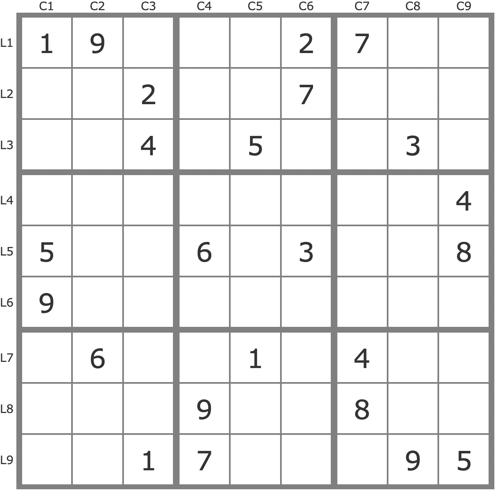
Résoudre la grille ... | Voir la résolution ... | Afficher les commentaires
Commentaires sur cette grille
De Robert Mauriès
(Publié le 24/04/2018)
Après réduction de la grille par les TB (5 placements), on résout la grille avec deux jeux de pistes successifs : JP(37L2C1) et JP(24L6C9).
- P(7L2C1) est invalide -> placements des 3 candidats de P(3L2C1).
- P(4L6C9) est invalide et P(2L6C9) couvre la grille.
De Francis Labetoulle
(Publié le 25/04/2018)
Bonsoir
Il faut donc trouver une autre voie que celle proposée par Robert, qu'une analyse préalable favorise nettement.
Apreès queques essais proposons une partition des candidats de L5C5:
P(36L5C5) couvre la grille.
Soit P2 = P(2LC5).
Les extensions P2.P(7L2C1) et P(7L2C4) conduisent à contradictions, sauf erreurs.
De Paolo
(Publié le 25/04/2018)
Bonsoir,
1) 5 placements par les TB iniziales.
P(4L5C1)=>couvre la grille
extension P’(4L5C1) avec les candidats de la case L2C1
2) P’(4L5C1).P(7L2C1)=> contradiction (deux 7 in C3)
3) P’(4L5C1).P(3L2C1)=> contradiction (L7C3=Ø)=>validation P(4L5C1)=>solution.
Ajouter un commentaire
Problème de sudoku
Apprenez à manier la technique des pistes par les problèmes de sudoku.PB-38 : Piste issue d'un ensemble
En utilisant la notion de piste issue d'ensemble, montrer que le 4 et le 9 de L1C7 peuvent être éliminés. De même montrer que l'on peut éliminer les 8 de L2C124.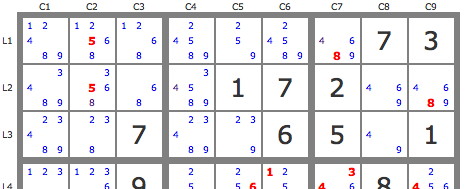
Voir la solution ...
Sudoku non-consécutif, diagonal et hyper-sudoku
L'assistant sudoku permet évidemment de traiter les grilles de sudoku non-consécutif, de sudoku-diagonal et d'hyper-sudoku.En savoir plus ...
En savoir plus ...
