S'identifier S'inscrire
assistant-sudoku.com
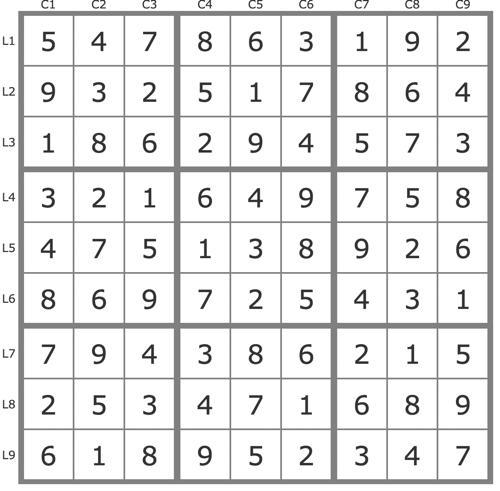
Grille Sudoku résolue
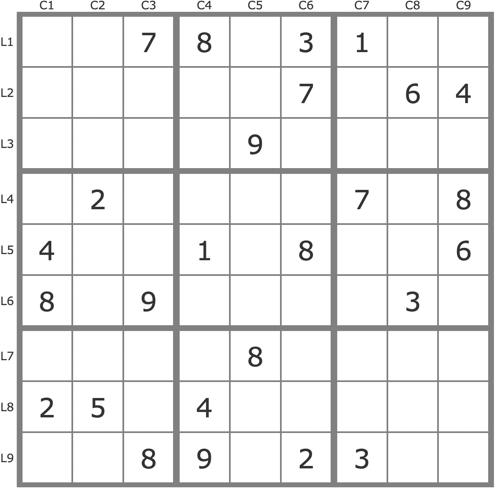
La grille -754Grille de niveau 2 TDP.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 17/06/2025)
Voir une résolution de taille 2 en cliquant sur le lien "Voir la résolution" ci-dessus.
De Francis Labetoulle
(Publié le 18/06/2025)
Bonjour Après quelques validations une analyse empirique m'oriente vers la case L8C5. Commençons par P = (3L8C5) qui se développe mais nécessite une bifurcation. J'opte pour P.(1L8C3) qui s'avère invalide, de même d'ailleurs que P.(-1L8C3). Par suite il faut éliminer 3L8C5 et ... fin. Je ne désespère pas de présenter peut-être une solution avec antipistes.
De Jean
(Publié le 18/06/2025)
Des premiers essais m'ont donné la solution sans difficulté à partir de la méthode des pistes, plus difficilement à partir d'un autre solveur. J'ai alors examiné sur la grille réduite des simplifications de base, la ligne 6 et la colonne 4. La ligne 6 comporte deux paires, ce qui a l'intérêt de réduire les combinaisons possibles. La colonne 5 a des cellules qui comporte toute le candidat 5 . A partir de cette approche, j'ai constaté que la solution s'obtenait en ne faisant que deux hypothèses : L6C4=7 et L4C4=6
De Francis Labetoulle
(Publié le 18/06/2025)
Re bonjour Ayant lu la solution proposée par Robert, je constate que mon cheminement est assez voisin. Donc voici un nouveau taille 2 (les antipistes sont hélas très longues): (-5L5C3): 0 donc validation de 5L5C3 (-7L5C2): 0 donc validation de 7L5C2 puis... fin
De Philippe
(Publié le 18/06/2025)
Bonjour, Paire 7 en C2 et B4 P(7L6C2) invalide - Validation dU 7 en L5C2 Paire 6-9 en L8C7 P(6L8C7) couvre la grille Unicité vérifiée par P(9L8C7).P(1L8C3) invalide P(9L8C7).P(1L8C6) invalide P(9L8C7).P(1L8C9) invalide Bonne journée
De François C.
(Publié le 19/06/2025)
Bonjour, Placements: 9L4C6, 3L3C9, 7L3C8, 8L8C8 Alignement: 9L8B9 => -9L7C7 -9L7C8 -9L7C9 Alignement: 7C1B7 => -7L7C2 -7L9C2 PISTE1 : 6L8C6->6L7C7->4L6C7->5L6C6->1L7C6->4L3C6->4L1C2->4L9C8->1L4C8->2L6C9->2L5C5->2L1C8 => 2C7 vide => -6L8C6 Placements : 1L8C6, 1L2C5 PISTE2 : 3L8C5->6L8C3->6L7C7->4L6C7->4L3C6->6L6C6->6L3C4->6L1C2 => 4L1 vide => -3L8C5 Placements jusqu’à la fin.
De Jean
(Publié le 19/06/2025)
Bonjour, je suis revenu sur la grille et lui ai appliqué une fois la méthode des pistes à partir de la paire 69 (P1=6, P2=9) en L8C7 https://easycaptures.com/fs/uploaded/1869/6219798765.jpg
De Robert Mauriès
(Publié le 19/06/2025)
@ Jean : Bonjour Jean. Oui, le 6L8C7 est un simple backdoor, c'est à dire que la piste (6L8C7) couvre la grille. Mais en revanche, la piste (9L8C7) n'aboutit pas directement à une contradiction, ce qui dans le cadre de la Technique des Pistes reste une construction incomplète sans une bifurcation de cette piste pour confirmer son invalidité. Merci tout de même pour votre proposition. Robert
De Robert Mauriès
(Publié le 19/06/2025)
Bonjour à tous. En principe, je n'utilise pas la notion de rectangle interdit lié à l'unicité de la solution, préférant prouver cette unicité. Voici tout de même des résolutions originales utilisant cette notion. 1) On exploite le croisement (éliminations, validations) des pistes issues de la paire 3L8. Pour avancer progressivement dans ce type de méthode, on remarque après quelques marquages de candidats que la piste (3L8C5) doit passer par le 3L2C3 pour éviter l'apparition du rectangle interdit RI=39L27C12. Cela suffit pour poursuivre éliminations et validations par croisement des deux pistes (3L8C3) et (3L8C5) jusqu'à résolution complète sans avoir à montrer laquelle des deux pistes est valide ou invalide. 2) Une autre approche permettant d'exploiter ce rectangle interdit potentiel RI est de construire l'anti-piste (-3L2C3,-3L8C3) qui conduit à RI, donc est invalide : (-3L2C3,-3L8C3)->3L8C5->7L8C9->9L8C7->6L7C7->4L6C7->4L3C6->4L7C3->RI->... Les deux pistes (3L2C3) et (3L8C3) sont donc conjuguées, et leur croisement suffit à résoudre la grille.
De Francis Labetoulle
(Publié le 20/06/2025)
Bonjour Pas d'antipistes à peu de pas chacune? En reprenant la solution de Robert on remarque que : P(-3L8C3) développée et 2L1C5 -> B5 vide de 2 donc -2L1C5 puis P(-3L8C3) invalide. Fin
De Robert Mauriès
(Publié le 20/06/2025)
@ Francis Labetoulle : Bonjour Francis. Une résolution avec des anti-pistes ne dépassant pas 7 enchaînements est possible, mais avec de nombreuses anti-pistes successives.
De Cenoman
(Publié le 20/06/2025)
Une solution en 6 pistes (simples ou presque...) Piste1 : 9L2C7->9L8C9->7L8C5->7L5C2 Et 3L7C4->3L2C2->... =>8L2 vide =>-9L2C7 (alignement => -9L1C2) Piste2 : 6L1C2->4L1C5->4L4C8->4L7C7->6L8C7->9L8C9->7L8C5->7L5C2->1L6C2->... =>1B6 vide =>-6L1C2; 7 placements Piste3 : 5L6C9->5L9C5->... => 5C6 vide =>-5L6C9 (alignement => -5L4C4 -5L5C5) Piste4 : 5L5C8->3L5C3->3L8C5->7L8C9->9L8C7->... =>9L5 vide =>-5L5C8 Piste5 : 5L5C7->59L1C89->2L1C5->29L5c78->... =>contradiction =>-5L5C7; 5 placements (paire 29L5C78 =>-2L5C5) Piste6 : 6L3C4->6L1C1->6L4C3->3L8C3->3L7C4->... =>L4C4 vide =>-6L3C4; placements jusqu'à la fin Voici les chaînes ou ternaires dont elles sont une traduction. 1. TERNAIRE (3)L257C2 (3-8)L2C2 = (8)L2C7 (3-7)L5C2 = L5C5 - L8C5 = (7-9)L8C9 = (9)L8C7 (3)L7C2 - L7C4 = (3-7)L8C5 = (7-9)L8C9=(9)L8C7 => -9L2C7 2. TERNAIRE (167)L6C2 (1)L6C2 - L6C9 = (1-4)L4C8 = L4C5 - L1C5 = (4)L1C2 (6)L6C2 (7)L6C2 - L5C2= L5C5 - L8C5 = (7-9)L8C9 = (9-6)L8C7 = (6-4)L7C7 = L6C7 - L4C8 = L4C5 - L1C5 = (4)L1C2 => -6L1C2 3. (5)L6C6 = L7C6 - L9C5 = L9C9 => -5L6C9 4. (5)L23C7 = L1C89 - (56=2)L1C15 - L5C5 = (29)L5C78 => -5L5C7 5. (9)L5C8 = L5C7 - L8C7 = (9-7)L8C9 = (7-3)L8C5 = L5C5 - (3=5)L5C3 => -5L5C8 6. TERNAIRE (6)L4C134 (6)L4C1 - L1C1 = L1C5 (6)L4C3 - (6=3)L8C3 - L8C5 = L7C4 - (3=6)L4C4 (6)L4C4 => -6L3C4
De Francis Labetoulle
(Publié le 21/06/2025)
@Bernard Cenoman Merci pour votre très belle résolution traduite en langage "Pistes". J'ai juste un petit souci concernant la piste 5 à partir de 2L1C5 que "j'ai remplacé" par ...2L1C5->3L5C3-> contradiction avec deux 7 sur L5. Je vais essayer de comprendre la notation des TERNAIRES.
De François C.
(Publié le 21/06/2025)
@ Cenoman : Bonjour Bernard, Pour ma part j’ai juste relevé une petite erreur : dans votre piste1 le 3eme candidat est 7L8C5 et non 7L7C5. Mais j’ai 2 questions : 1) Est-ce que vous trouvez les chaînes (AIC) et les ternaires (kraken) de façon systématique en utilisant la méthode « Full tagging » de Champagne ? Je n’ai fait que survoler cette méthode il y a 10 ans, mais j’ai vu que vous l’aviez utilisée copieusement pendant quelques années sur sudokuvariante.forumactif.com 2) En parlant de vos pistes vous dites « voici les chaînes ou ternaires dont elles sont une traduction ». Je ne pense pas qu’il existe une méthode pour déduire une piste d’une chaîne (AIC) et encore moins d’un ternaire (kraken). D’autant plus que vos pistes sont toutes les plus courtes possibles, pour des cibles données. Avez-vous écrit un programme ou utilisé SudokuRules de D. Berthier pour créer vos pistes ?
De Cenoman
(Publié le 21/06/2025)
@Francis Labetoulle, Merci Francis pour l'appréciation ! Concernant la piste 5, si L1C5=2, alors L5C5<>2, d'où L5C78=29, compte tenu du blocage des 9L5 en C78. Donc L5C7=2 ou L5c7=9 => L5C7<>7, cqfd. Mais OK, pour votre alternative. Notation des Ternaires: Le ternaire part de trois candidats liés par un lien fort (trois candidats d'une même cellule, ou d'un(e) même ligne ou bloc) L'un des trois au moins doit être vrai. Les trois chaînes démontrent chacune que si la cible (l'élimination) est vraie, les trois sont faux, donc la cible est fausse. Notez que chaque chaîne se termine par un candidat en conflit avec l'élimination. Dans mon écriture, le lien fort entre les trois candidats racines est implicite. On pourrait rappeler ce lien en écrivant (par exemple pour le ternaire 6): TERNAIRE (6)L4C134 ||(6)L4C1 - L1C1 = L1C5 ||(6)L4C3 - (6=3)L8C3 - L8C5 = L7C4 - (3=6)L4C4 ||(6)L4C4 => -6L3C4
De Cenoman
(Publié le 21/06/2025)
@François C. Bonjour, Merci pour la détection de l'erreur. (Comme je traduis "manuellement", je fais des fautes de frappe...) La piste1 est bien : 9L2C7->9L8C9->7L8C5->... EDIT : erreur rectifiée dans le message originel. Question 1. Oui, j'utilise le marquage généralisé pour trouver les chaînes et les logiques multiples (ternaire pour un ensemble fort à 3 candidats, quaternaire si 4 candidats, etc.), jusqu'aux réseaux de logiques multiples. Le marquage est un multi-coloriage avec un nombre illimité de couleurs, ou plus précisément de paires de couleurs. Son point de départ est la notion de conjugués (autrefois on les appelait 'jumeaux'). Une marque (un 'tag') est la variable logique de tous les conjugués Vrais ou Faux ensemble. Une marque est en conflit avec une autre dès que deux candidats de l'une et de l'autre sont en conflit natif. Les conflits se propagent par dérivations successives depuis deux marques opposées (qui sont donc conjuguées). L'extension "full tagging" a consisté à introduire dans ce processus les conflits fournis par ce que champagne avait alors appelé les pseudo-cases, aujourd'hui nommées AHS (almost hidden sets, soit quasi ensembles cachés). Lectures disponibles: - en français, "Memento Marquage" de jeanlé, https://sudokuvariante.forumactif.com/t480-marquage - en anglais, le fil "Full Tagging" de champagne, http://forum.enjoysudoku.com/full-tagging-t5624.html Les écrits de champagne en français ont disparus avec la fermeture des pages perso d'Orange... Question 2. Pour le moment je n'ai pas encore écrit de programme de traduction, et je ne vois pas en quoi SudoRules pourrait m'être utile (il me faudrait faire deux traductions au lieu d'une). Je ne suis pas d'accord pour dire qu'il n'existe pas de méthode pour déduire une piste d'une chaîne ou d'une logique multiple. Une Piste est un enchainement de vérités, une chaîne est une alternance de vérités et de négations. En ne gardant que les vérités et en traitant spécifiquement les effets de mémorisation, on a une piste ou presque. Cela ne doit être bien compliqué, la preuve, c'est que j'y arrive ! Il se peut que certaines logiques multiples ne soit pas traduisibles en une seule piste, mais dans ces cas, il reste la ressources des jeux de pistes, comme Robert l'a suggéré plusieurs fois.
De Cenoman
(Publié le 21/06/2025)
Désolé pour le double postage de ma réponse à Francis. Double supprimé, grace au tuyau de Robert; Merci.
De François C.
(Publié le 22/06/2025)
@ Cenoman : Merci pour vos explications, c’était surtout pour savoir si le fulltaging était encore utilisé par quelqu’un. En tous cas bravo pour vos pistes calculées au plus court car il y en a quand même une de longueur 9.
De Francis Labetoulle
(Publié le 22/06/2025)
Bonjour à tous et désolé concernant "mon petit souci" pour la piste 5, lié sans doute à mon habitude de pratiquer une approche par piste laissant les candidats en place jusqu'à invalidité constatée. Pour information, avant de me lancer dans le full tagging, la référence technique d'Hodoku utilise la notation pratiquée, me semble-t-il, par Bernard et j'essaie de m'y adapter, en commençant à appréhender les ternaires! D'après "chatGpt" Michel Champagne a publié un livre sur la théorie du Sudoku, en 2006. Ma recherche sur le net n'a rien donné. Bonne soirée
De Cenoman
(Publié le 22/06/2025)
@Francis Labetoulle Bonjour Francis, Il ne faut croire tout ce que dit chatGPT. 'champagne' est un pseudo. Son vrai nom est donné dans le fil 'full tagging', où il renvoie vers sa page perso Orange. Il était très actif dans les anciens forums français (Figaro, sudokufactory) A ma connaissance, il n'a jamais publié de livre. Ajout1 - Petit conseil: commencez par le Mémento de jeanlé. Très bien fait, pour commencer par le marquage manuel. Il m'a permis d'en déduire ensuite l'algorithme principal de mon solveur. Ajout2 - Je ne connais pas Hodoku, mais je suppose qu'il utilise comme moi, la notation dite "Eureka" pour les chaînes. (Eureka est un ancien site anglophone de sudoku, maintenant disparu)
De Francis Labetoulle
(Publié le 23/06/2025)
@Bernard Cenoman Bonjour et merci pour vos précieux conseils que je vais suivre dans l'ordre préconisé.
Ajouter un commentaire
La solution
Après réduction de la grille par les TB (4 placements de candidats uniques et quelques éliminations par alignements), on exploite la case L8C3 :
P(1L8C3) et P(6L8C3) sont invalides, tandis que P(3L8C3) couvre la grille via le doublet 29L1C89.
En principe, je n'utilise pas la notion de rectangle interdit lié à l'unicité de la solution, préférant prouver cette unicité.
Voici tout de même des résolutions originales utilisant cette notion.
1) On exploite le croisement (éliminations, validations) des pistes issues de la paire 3L8. Pour avancer progressivement dans ce type de méthode, on remarque après quelques marquages de candidats que la piste (3L8C5) doit passer par le 3L2C3 pour éviter l'apparition du rectangle interdit RI=39L27C12. Cela suffit pour poursuivre éliminations et validations par croisement des deux pistes (3L8C3) et (3L8C5) jusqu'à résolution complète sans avoir à montrer laquelle des deux pistes est valide ou invalide.
2) Une autre approche permettant d'exploiter ce rectangle interdit potentiel RI est de construire l'anti-piste (-3L2C3,-3L8C3) qui conduit à RI, donc est invalide :
(-3L2C3,-3L8C3)->3L8C5->7L8C9->9L8C7->6L7C7->4L6C7->4L3C6->4L7C3->RI->...
Les deux pistes (3L2C3) et (3L8C3) sont donc conjuguées, et leur croisement suffit à résoudre la grille.
On trouvera dans le forum d'autres résolutions intéressantes.
 En savoir plus ...
En savoir plus ...




