S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -753Grille de niveau 1 TDP, donc que l'on peut résoudre avec un seul jeu de pistes.
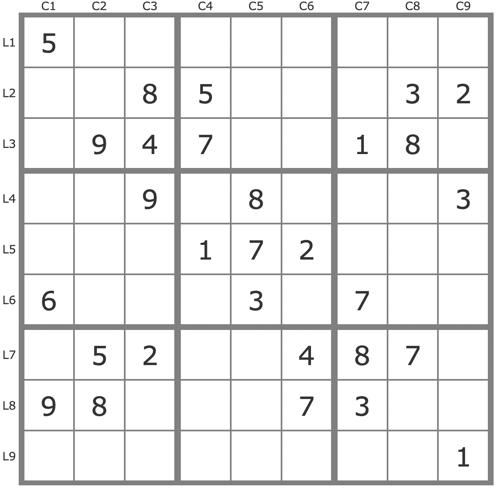
Commentaires sur cette grille
De Robert Mauriès
(Publié le 09/06/2025)
Une anti-piste suffit pour résoudre la grille après sa réduction par les TB (5 placements uniques et quelques éliminations) : (-5L4C6)->6L4C6->5L6C6->5L5C3->[3L5C2 et 3L1C3->6L8C3]->4L9C2->4L4C1->... => L4C4 vide => L4C6=5 et fin. A noter Francis, en référence à votre question sur le sujet, qu'il s'agit là d'une chaîne à mémoire. Plus de détails en cliquant sur "Voir la résolution".
De Jean
(Publié le 10/06/2025)
Bonjour, La résolution effectuée fait l'objet de l'image https://easycaptures.com/fs/uploaded/1860/6491041550.jpg Elle comporte 4 captures. Capture 1 ( GR 1) après les simplifications de base, j'ai adopté les pistes 1 et 2 en L4C4 et L6C4 ; P1 est invalide . Capture 2 (GR 2) J'ai ensuite adopté les pistes 6L3C5 et 6 L7C5 . P1 est invalide. . Capture 3 ( GR 2a) Il m'a paru bon de nettoyer les cellules qui avaient une solution P1 et P2 Capture 4 (GR2b) J'ai commencé à validé les candidats prédéterminés par le solveur ( en rouge) . La solution apparaît sans qu'il soit nécessaire de les valider tous et de passer à la phase validation de P2 Sans avoir fait le tour des possibilités du solveur ( antipistes etc...) je constate que cet outil permet d'arriver rapidement à la solution et de diffuser les résultats sous une forme facilement transmissible. L'on éprouve cependant aussi de l'intérêt pour des résolutions plus graphiques, qui supposent la connaissance de schémas de résolution, même si ces résolutions demandent souvent plus de travail
De Cenoman
(Publié le 10/06/2025)
Après TB: TERNAIRE (346)r9c2 (3)r9c2 - r5c2 = r5c3 - (3=61)r18c3 - (1=5)r6c3 - r6c6 = (5)r4c6 (4)r9c2 - r9c1 = r4c1 - (4=6)r4c4 (6)r9c2 - (6=1)r8c3 - (1=5)r6c3 - r6c6 = (5)r4c6 => -6r4c6; placements jusquà la fin Traduction en antipiste: (-5r4c6)->5r6c6->1r6c3->6r8c3->3r1c3->3r5c2->4r9c2->4r4c1->6r4c4->... => -6r4c6; placements jusquà la fin
De Robert Mauriès
(Publié le 10/06/2025)
@ Jean : Bonsoir Jean, Votre premier jeu de pistes issues des 4C4 suffit à la résolution, car P(4L6C4) couvre la grille. Le second jeu de pistes n'est donc pas utile.
De Robert Mauriès
(Publié le 10/06/2025)
@ Cenoman : Bonsoir Bernard. Merci pour votre résolution avec ce Kraken, l'occasion pour moi de donner une interprétation avec un jeu de 3 pistes issues des 3 candidats de L9C2 : 3L9C2->3L5C3->5L6C3->5L4C6->... 4L9C2->4L4C1->6L4C4->5L4C6->... 6L9C2->1L8C3->5L6C3->5L4C6->... => L4C6=5 et fin, et de rappeler que la technique des pistes ne s'applique pas qu'à des jeux de deux pistes.
De Francis Labetoulle
(Publié le 11/06/2025)
Bonjour Après quelques placements, voici un cheminement abusant de la mémorisation: P'(1L8C5) = (-1L8C5) ->...a,b et c: a->6L9C2, b->2L3C1->6L3C5 et c->5L6C3->5L4C6-> 6L4C4 donc invalidité car B8 est vide de 6, ce qui valide 1 L8C5 et permet de nombreux placements. P'(3L3C1) = (-3L3C1) ->4L4C1 ->...d et e: d-> 3L5C2->5L5C3, e->6L4C5-> 5L4C6 donc invalidité car B6 est vide de 5, ce qui valide 3L3C1 et ... couvre la grille. Remarques: -J'aurais dû profiter de la notation de Robert pour la "mémorisation". J'en prends note pour la prochaine fois. -Ce ternaire L9C2 ou encore ces 3 pistes issues de L9C2, c'est vraiment magnifique. Bravo!
De Philippe
(Publié le 11/06/2025)
Bonjour Une anti-piste un peu longue à partir de 3L5C3 (-3L5C3)->5L5C3->1L6C3->6L8C3->3L1C3->2L3C1->2L8C4->4L8C9->6L3C5->3L3C6->5L8C8->1L8C5->9L7C5->6L7C9->9L5C9->3L5C2->4L9C2->2L6C2->4L6C8->4L4 absent->3L5C3 validé Une anti-piste un peu plus courte toujours à partir de 3L5C3 donne le même résultat (-3L5C3)->5L5C3->1L6C3->6L8C3->4L8C9->3L5C2->4L9C2->4L4C1->6L4C4->5L4C6->2L4C7->2L8C4->5L8C8->5L6 absent->3L5C3 validé La grille tombe par effet domino avec en cours du traitement les 2 techniques intermédiaires (voir : 1 L78C5 et 6 L3C56) Bonne journée
De Robert Mauriès
(Publié le 11/06/2025)
@ Francis Labetoulle : Bonjour Francis, La technique des pistes appliquée à un nombre de pistes n est en fait la technique des pistes appliquée à un ensemble E={A1, A2,..., An}, car P(E) est représentée par l'intersection des P(Ai). Ainsi, si P'(E) est invalide, les candidats de P(E) sont solutions de la grille et les candidats qui voient toutes les pistes P(Ai) peuvent être éliminés. Dans le cas de la case L9C2, en prenant E=346L9C2, on a évidemment P'(E) invalide, d'où P(E)={5L4C6,...}=intersection de P(3L9C2), P(4L9C2) et P(6L9C2) est solution. Les Krakens se construisent toujours à partir d'un ensemble E qui est soit formé de tous les candidats d'une case, soit formé de tous les candidats de même occurrence d'une zone (ligne colonne ou bloc). Il en va donc de même de l'interprétation que l'on peut en faire avec des pistes puisque P'(E) est invalide dans tous ces cas. Encore faut-il trouver les "bons ensembles" E.
De Robert Mauriès
(Publié le 11/06/2025)
@ Philippe : Bravo Philippe de vous essayer aux anti-pistes !
De Francis Labetoulle
(Publié le 12/06/2025)
@Robert Petite demande de mise au point de notations sur les anti-pistes avec mémorisation sur un exemple partant du bloc B5 (incontournable me semble-t-il pour les tailles 1). Je suppose ne pas avoir lu la solution ! Il s'agit de montrer que 6L4C6 est invalide, dans les meilleurs délais, en partant donc de (-5L4C6) : 6L4C6->3L3C6->2L3C1; puis je choisis [1L8C3 ou 6L8C3] Est-ce licite un « ou » plutôt qu’un « et »? Supposons-le. 1L8C3 -> 5L6C3 : donc invalidité car absence de 5 dans B5; 6L8C3 -> 1L7C1 ->7L2C1 -> 4L4C1 (avec 2L3C1...) donc invalidité car case L4C4 vide et fin. Cette rédaction est-elle recevable et ce cheminement avec mémorisation est-il "convenable"? Merci pour l'information sur les krakens et le lien avec la méthode des pistes.
De Robert Mauriès
(Publié le 12/06/2025)
@ Francis Labetoulle : Bonsoir Francis, votre question est intéressante. Elle me donne l'occasion de préciser la différence entre le "et" et le "ou" dans la construction d'une piste. - Le "et" dans le processus de construction d'une piste P(E) indique que la piste passe par plusieurs candidats Ap+1, Ap+2, ... dès lors qu'elle passe par le candidat Ap, cela par la seule application des TB. Cela s'écrit P(E): A1->...->Ap->[Ap+1 et Ap+2 et ...]->Ap+k->... - Le "ou" ne fait pas partie du processus de construction d'une piste par la seule application des TB. Le "ou" indique que l'on utilise une bifurcation. Ce n'est donc pas une piste que l'on construit avec le "ou" mais un arbre de résolution, c'est à dire une piste et ses branches P-pistes. Il faudrait alors représenter cela par un schéma comme ceci pour une piste qui passerait par Ap+1 "ou" Ap+2 : -> Ap+1->... P(E):A1->...Ap | -> Ap+2->... Rien n'interdit évidemment d'utiliser le "ou", donc une bifurcation, mais alors on augmente le niveau de résolution. Dans l'exemple que vous donnez, on doit en déduire que le niveau de résolution est de 2.
Ajouter un commentaire
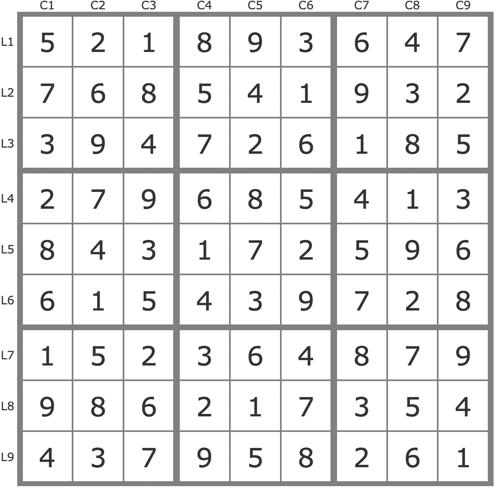
La solution
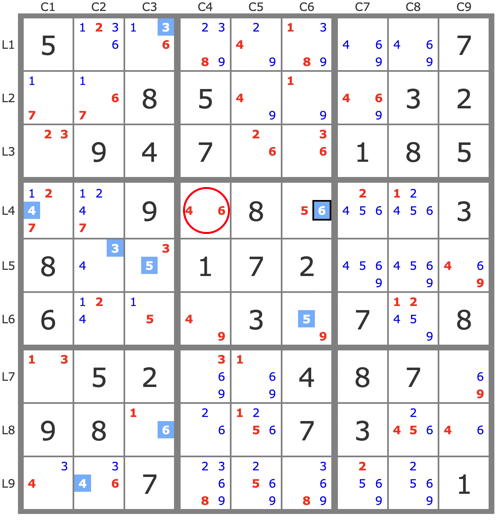
Après simplification de la grille par les Techniques de Base (5 placements uniques et quelques éliminations), un seul jeu de pistes en vient à bout, par exemple au départ de la paire 56L4C6 :
P(5L4C6) couvre la grille
P(6L4C6) = 6L4C6->5L6C6->5L5C3->[3L5C2 et 3L1C3->6L8C3]->4L9C2->4L4C1->... => L4C4 vide => P(6L4C6) invalide
 En savoir plus ...
En savoir plus ...




