S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -752Grille de niveau 2 TDP.
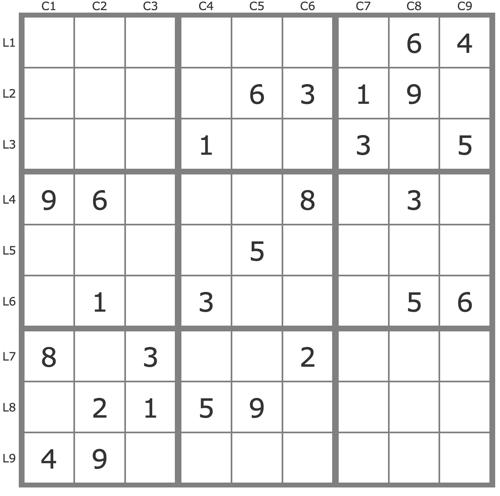
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 04/06/2025)
Bonjour Voici un taille 2 (J'ai encore quelques difficultés avec le choix judicieux des antipistes pour la méthode des éliminations successives...). Sauf erreur : P'(1L9C6):0 P(1L9C6)=P. Après quelques validations et simplifications: P.P(6L8C6): 0 puis P.P(4L8C6) : 1. Le béotien que je suis profite de l'occasion pour poser quelques questions "lambda" après avoir lu avec grand intérêt les commentaires de la grille 751: -quelle est la bonne écriture pour une antipiste : P'(5L1C3) ou (-5L1C3) ou (**...L1C3) et généralisation pour groupes? -peut-on utiliser, dans la méthode des antipistes, la piste conjuguée de cette antipiste pour effectuer des simplifications et validations, et si oui jusqu'à quel niveau ? -qu'appelle-t-on précisément mémorisation? S'agit-il d'un marquage (par couleurs par exemple) des divers éléments de pistes ou chaînes? Bonne journée en attendant la fin de l'orage!
De Robert Mauriès
(Publié le 04/06/2025)
@ Francis Labetoulle : Bonjour Francis, il n'y a que de bonnes questions, rassurez-vous ! Question notation P'(E) ou (-E) sont des notations correctes. J'utilise les deux, même si plus récemment je préfère utiliser (-E). Cela reste au choix de chacun. De même on peut utiliser P(E) ou (E). On parle de chaîne avec mémorisation, ou chaîne à mémoire, lorsque le nième élément de la chaîne dépend de certains éléments précédents le (n-1)ième élément. Les Whips et les Braids sont des chaînes à mémoire. Les pistes (ou anti-pistes) sont des chaînes à mémoire en général, notamment les pistes ou anti-pistes longues. Mais on peut, du moins pour des grilles pas trop difficiles, rechercher comme Bernard (Cenoman) des chaînes (donc des pistes) sans mémoire pour résoudre (voir ci-dessous pour la grille 751).
De Philippe
(Publié le 04/06/2025)
Bonjour Pistes issues de la paire de 6 de L3 PBleu à partir du 6L5C4 PRouge à partir du 6L5C6 Des suppressions et 6 validations La piste rouge couvre la grille L'unicité est vérifiée par les 2 contradictions sur les 2 candidats de la paire 1/7 de L9C6 Bonne Journée
De Robert Mauriès
(Publié le 05/06/2025)
@ Philippe : Bonjour Philippe. Belle résolution par croisement des pistes que celle que vous proposez avec la vérification de l'unicité. Dans le formalisme TDP on peut écrire aussi : P(6L5C4).P(1L9C6) invalide P(6L5C4).P(7L9C6) invalide P(6L5C6) couvre la grille. Merci pour votre participation régulière à ce forum. Robert
De Jean
(Publié le 05/06/2025)
Bonjour . Validation de 11 candidats (en rouge) indiqués par la grille détaillée. Suppression type cerf-volant de 1 en L9C4, 8 en L2C3. Application de la méthode des pistes trois fois en ... En L6C1 , 2(P1) 7(P2) , P2 invalide , P1 validée; En L9C3 , 6(P1), 7(P2) , P2 invalide , P1 validée; En L9C6, 1(P1) , 7(P2) , P2 invalide , P1 validée. Suppression d'occurrences, du fait de paires dans la zone : 7 en L7C789, L67C5, 7 et 4 en L13C3, 2 en L12C4, 7 en colonne 9 (hors des 2 paires 27), Validé 8 en L2C9, 2 en L2C3 ; du fait d'une paire 27 en colonne 8 suppression de ces 2 valeurs en L5C8. Suppression type cerf volant de 4 en L7C7. Méthode des pistes une 4e fois en L9C8 2(P1) 7(P2) P1 invalide Swordfish de 4 en L56C3, L67C5, L57C8 XY wing de 4 en L27C4, L8C6 Solution
De Robert Mauriès
(Publié le 05/06/2025)
Pour faire différent, voici une résolution basée sur des anti-pistes courtes (7 enchaînements maximum) sans chercher à en minimiser le nombre. Après placements de 11 candidats uniques, on exploite les différentes paires de la grille : (-6L9C3)->6L9C6->6L5C4->9L1C4->9L3C3->... => -6L3C3 => 4 placements (-1L4C9)->1L4C5->1L9C6->... => -1L9C9 (-8L2C9)->8L5C9->8L6C3->... -8L2C3 (-9L3C3)->9L3C6->9L6C7->8L6C3->... -8L3C3 (-9L1C4)->[9L5C4->6L5C6->1L4C5]->2L4C4->... => -2L1C4 (-2L9C9)->7L9C9->1L9C6->1L4C5->2L4C9->... -2L25C9 (-7L9C89)->7L9C6->1L5C6->6L5C4->6L7C7->9L7C9->... => -7L7C79 (-9L1C4)->9L5C4->6L5C6->1L4C5->2L4C4->7L1C7->... => -7L1C4 => 2 placements (-4L3C6)->7L3C6->1L9C6->47L67C5->... -4L3C5 (-6L5C4)->6L5C6->4L8C6->4L2C4->... -4L5C4 (-2L4C45)->2L5C4->6L5C6->[1L4C5 et 4L8C6->4L2C4]->4L4C7->... =>-2L4C7 (-1L4C5)->1L5C6->1L4C9->9L7C9->9L5C7->2L5C8->2L3C5->... => -2L4C5 => 1 placement (-2L9C9)->2L9C8->2L1C7->2L5C4->6L5C6->4L8C6->7L3C6->7L2C9->... => -7L9C9 => 2 placements (-7L9C8)->1L9C8->[1L5C6 et 9L7C9]->9L5C7->2L1C7->7L2C9->... => -7L9C6 et fin
De Cenoman
(Publié le 05/06/2025)
Une solution 'chaînes et ternaires', avec une tentative de traduction en TDP. Après TB, 1. (7=21)L9C89 - L9C6 = (1-6)L5C6 = L5C4 - L7C4 = (69)L7C79 => -7 L7C79 2. (1)L9C6 = L5C6 - L4C5 = L4C9 => -1 L9C9 3. (9=274)L6C156 - L4C45 = L4C7 - (4=6|9)L7C7 - (69)L7C49 = (6)L5C49=> -9 L5C4 4. (2=71)L49C9 - L4C5 = L5C6 - (1=7)L9C6 - (7=2)L9C9 => -2 L25C9 5. TERNAIRE (4)L578C8 (4)L5C8 - (4=78^)L5C23 - L6C3 = (8)L6C7 (472-1)L7C8.L9C89 = (1-9)L7C9 = (9^-8)L5C9 = (8)L2C9 (4-8)L8C8 = L8C7* - L6C7 = (8-7)L6C3 = (7)L5C23 => -7 L5C9^, -8 L1C7* 6. TERNAIRE (7)L7C45.L9C6 (7-6)L7C4 = (6-2)L5C4 = (2)L4C45 (7)L7C5 - (7=4)L6C5 - L4C45 = (4)L4C7 (7-1)L9C6 = (1-6)L5C6 = (6-2)L5C4 = (2)L4C45 => -2 L4C7 7. (7=4)L3C6-(4=6)L8C6-L5C6=(6-2)L5C4=L5C78-L4C9=(2-7)L9C9=(7)L79C8 => -7 L3C8 8. TERNAIRE (247)L2C4 (2)L2C4-L2C3=L1C3-L1C7=(2)L3C8 (4)L2C4-(4=7)L3C6-(7=1)L9C6-L5C6=L4C5-(1=278)L249C9 (7)L2C4-(7=8)L2C9 =>-8L3C8; placements jusqu'à la fin Traduction (avec pistes, antipistes, jeu de pistes, et même... mémorisation) AP1 (-7L9C89)->(21)L9C89->1L5C6->6L5C4->6L7C7->9L7c9->... => -7 L7C79 AP2 (-1L9C6)->L5C6->L4C9->... => -1 L9C9 P3 9L5C4->6L7C4 Et 9L7C9->4L7C7->4L4C45->27L6C15->9L6C6->...contradiction => -9L5C4; 6 placements AP4 (-2L9C9)->7L9C9->1L9C6->1L4C5->72L49C9->... =>-2L25C9 JP5 4L5C8->87L5C23->8L6C7 4L7C8->8L8C8->6L8C7->9L7C7->9L5C9->8L2C9 4L8C8->8L8C7->8L6C3->47L5C23 => -7L5C9, -8L1C7 (en conflit avec les trois pistes) P6 2L4C7->2L5C4->[6L7C4 ET 6L5C6->1L9C6]->7L7C5->4L6C5->4L4C7->...contradiction => -2L4C7 AP7 (-7)L3C6->4L3C6->6L8C6->6L5C4->2L5C78->2L9C9->7L79C8->... => -7L3C8 P8 8L3C8->[2L1C7->2L2C3 ET 7L2C9]->4L2C4->7L3C6->1L9C6->1L4C5->27L49C9->8L2C9->...contradiction => -8L3C8; placements jusqu'à la fin
De François C.
(Publié le 06/06/2025)
Bonjour, Avec 6 pistes courtes: Placements: 1L1C1, 3L1C2, 5L4C3, 5L1C6, 3L5C1, 3L8C9, 3L9C5, 5L9C7, 5L7C2, 5L2C1, 8L9C4 PISTE1: 7L7C7->6L7C4->6L5C6->6L9C3->7L9C6 => 1C6 vide => -7L7C7 PISTE2: 9L3C6->9L6C7->9L5C4->6L7C4->4L7C7->4L5C8->4L6C3 => 8L6 vide => -9L3C6 Placements: 9L3C3, 9L1C4, 6L3C1, 7L8C1, 2L6C1, 6L9C3 PISTE3: 2L4C5->1L5C6->6L5C4->6L7C7->9L7C9->9L5C7->2L1C7 => 2L3 vide => -2L4C5 Alignement: 2C5B2 => -2L2C4 Paires: 47B2p49 => -7L1C5 -4L3C5 -7L3C5 PISTE4: 7L5C9->7L6C3->4L6C5->9L6C6->9L5C7->7L1C7->2L4C7 => 4L4 vide => -7L5C9 PISTE5: 1L7C5->7L9C6->7L2C4->4L3C6->4L7C4->7L7C8->7L4C9 => 1L4 vide => -1L7C5 Placements: 1L4C5, 1L9C6 Alignement: 7L9B9 => -7L7C8 -7L7C9 Paires: 27C9L49 => -2L2C9 -7L2C9 -2L5C9 Placements: 8L2C9, 2L2C3 Alignement: 4C3B4 => -4L5C2 Paires: 27C8L39 => -2L5C8 -7L5C8 PISTE6: 6L7C7->6L5C4->2L5C7->7L1C7->8L1C3->8L6C7 => 9C7 vide => -6L7C7 Placements jusqu'à la fin.
De Alain
(Publié le 06/06/2025)
P(7L6C1) invalide, d'où 2L6C1 P(7L3C1) invalide, d'où 6L3C1 P(4L8C6) couvre la grille
Ajouter un commentaire
La solution
Voir les résolutions proposées dans le forum par grilles.
Voici une résolution basée sur des anti-pistes courtes (7 enchaînements maximum) sans chercher à en minimiser le nombre.
Après placements de 11 candidats uniques, on exploite les différentes paires de la grille :
(-6L9C3)->6L9C6->6L5C4->9L1C4->9L3C3->... => -6L3C3 => 4 placements
(-1L4C9)->1L4C5->1L9C6->... => -1L9C9
(-8L2C9)->8L5C9->8L6C3->... -8L2C3
(-9L3C3)->9L3C6->9L6C7->8L6C3->... -8L3C3
(-9L1C4)->[9L5C4->6L5C6->1L4C5]->2L4C4->... => -2L1C4
(-2L9C9)->7L9C9->1L9C6->1L4C5->2L4C9->... -2L25C9
(-7L9C89)->7L9C6->1L5C6->6L5C4->6L7C7->9L7C9->... => -7L7C79
(-9L1C4)->9L5C4->6L5C6->1L4C5->2L4C4->7L1C7->... => -7L1C4 => 2 placements
(-4L3C6)->7L3C6->1L9C6->47L67C5->... -4L3C5
(-6L5C4)->6L5C6->4L8C6->4L2C4->... -4L5C4
(-2L4C45)->2L5C4->6L5C6->[1L4C5 et 4L8C6->4L2C4]->4L4C7->... =>-2L4C7
(-1L4C5)->1L5C6->1L4C9->9L7C9->9L5C7->2L5C8->2L3C5->... => -2L4C5 => 1 placement
(-2L9C9)->2L9C8->2L1C7->2L5C4->6L5C6->4L8C6->7L3C6->7L2C9->... => -7L9C9 => 2 placements
(-7L9C8)->1L9C8->[1L5C6 et 9L7C9]->9L5C7->2L1C7->7L2C9->... => -7L9C6 et fin
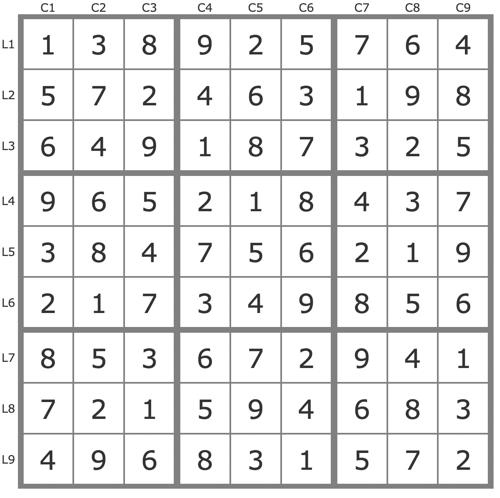
 En savoir plus ...
En savoir plus ...




