S'identifier S'inscrire
assistant-sudoku.com
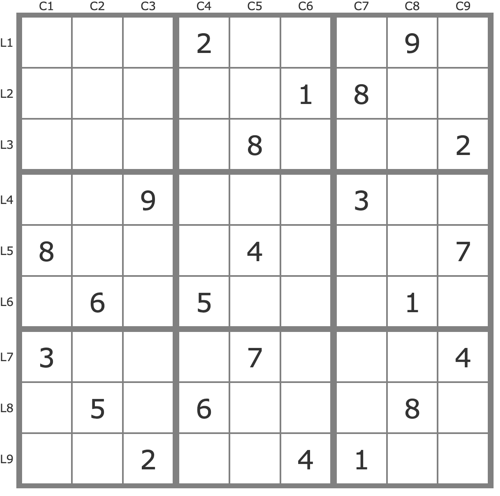
Grille Sudoku résolue
La grille -750Cette grille est extrêmement difficile à résoudre (niveau TDP = 11).
Elle devient plus facile si le 5L9C9 est ajouté comme dévoilé (niveau TDP = 3).
Sa difficulté est encore réduite si, après le 5L9C9, le 5L5C3 est ajouté comme dévoilé aussi (niveau TDP = 1).
Commentaires sur cette grille
De François C.
(Publié le 20/05/2025)
Bonjour, résolution de la Grille avec +5L9C9 utilisant 6 pistes de longueur <= 13 : Placement: 5L7C6 Alignement: 2L7B9 => -2L8C7 Alignement: 8C6B5 => -8L4C4 PISTE1: 6L9C8->3L8C9->6L2C9->9L6C9->37C8L23->4L4C8->2L6C7->3L6C5->9L9C5->5L2C5->6L1C5->5L4C1->47C1L16 => L9C1 vide => -6L9C8 Placement: 6L9C1 Paires cachées: 26L7C78 => -9L7C7 Alignement: 9B9L8 => -9L8C1 -9L8C5 -9L8C6 Alignement: 9C1B1 => -9L2C2 -9L3C2 PISTE2: 4L6C3->4L4C8->5L4C1->4L8C1->7L1C1->2L6C1->9L6C7->7L8C7 => 7C3 vide => -4L6C3 PISTE3: 4L6C1->4L4C8->5L4C1->7L1C1->1L8C1->9L3C1->AL-9C6B5->13L5C34-> 2L5C2->17L4C24 => 1C5 vide => -4L6C1 Placement: 4L6C7 Alignement: 4L1B1 => -4L2C1 -4L2C2 -4L2C3 -4L3C1 -4L3C2 -4L3C3 Triplets: 256C8L457 => -5L2C8 -6L2C8 -5L3C8 -6L3C8 Alignement: 5C8B6 => -5L5C7 PISTE4: 3L9C5->3L8C9->9L6C9->2L6C5->1L8C5->6L4C5->5L1C5->47C1L18 => L6C1 vide => -3L9C5 Placements: 9L9C5, 9L7C2 Paires cachées: 89L6C69 => -2L6C6 -3L6C6 -7L6C6 Alignement: 7L6B4 => -7L4C1 -7L4C2 PISTE5: 3L5C3->7L6C3->3L6C5->56L2C35->3L2C9->3L8C6->8L9C4->8L1C2 => 3L1 vide => -3L5C3 PISTE6: 7L9C8->8L9C2->1L7C3->8L1C3->4L8C3->7L8C1->2L6C1->7L6C3->3L5C2->1L5C4->7L4C4->7L2C2 => 2L2 vide => -7L9C8 Placements jusqu’à la fin.
De Francis Labetoulle
(Publié le 22/05/2025)
Bonjour J'ai obtenu la solution et l'unicité en partant de la case L8C9, sans grand intérêt et avec un nombre bien trop élevé de ramifications invalides. Je ne donne que le cheminement de la solution : 9L8C9 puis 5L9C9 puis 9L6C6. Je suis curieux de voir comment on peut résoudre cette grille par éliminations successives (et sans logiciel évidemment).
De Robert Mauriès
(Publié le 22/05/2025)
@ Francis Labetoulle : Bonjour Francis, Cette grille 750 ne peut pas être résolue pas-à-pas avec des pistes ou des anti-pistes, même en ne se limitant pas sur la longueur des enchaînements, car elle n'est pas de profondeur 1. Elle est de profondeur 3, ce qui nécessite obligatoirement l'utilisation, sous une forme ou une autre, des bifurcations. Tout juste peut-on faire quelques éliminations préalables dans le bloc 1, mais ensuite l'utilisation des arbres de résolution est incontournable. C'est la raison aussi pour laquelle j'ai proposé d'ajouter le 5L9C9 pour la rendre accessible à une résolution pas-à-pas.
De Francis Labetoulle
(Publié le 22/05/2025)
@Robert Merci pour vos précisions. Je me permets de vous poser deux questions : 1. Comment savoir que le niveau TDP minimal est de10? J'en suis bien loin et la probabilité du bon choix doit être bien faible ? 2. L'application des techniques préconisées par Denis Berthier permet-elle la résolution de cette grille et si oui l'équivalence supposée avec la méthode des antipistes nécessite, me semble-t-il, que l'on utilise nécessairement des bifurcations pour celles-ci jusqu'à obtention d'invalidités, ce qui, selon l'analogie avec le jeu d'échecs, est digne d'un grand maître ! Il faut trouver des candidats "judicieux" à éliminer. Ai-je bien appréhendé le protocole ? Désolé de vous poser de telles questions bien naïves qui ne demandent pas nécessairement de réponses. Bonne soirée
De Robert Mauriès
(Publié le 22/05/2025)
@ Francis Labetoulle : Le niveau TDP est obtenu par le logiciel de François. A la main ce résultat est difficile à atteindre. Ce n'est pas 10 mais 11 d'ailleurs. Les whips et braids de Denis Berthier, dont on peut donner une équivalence avec des pistes ou des anti-pistes, ne permettent pas la résolution de cette grille qui demande des outils plus puissants comme les Bp-braids. Les Bp-braids se composent de braids à l'intérieur des braids, une composition de braids en somme, comme on peut faire des pistes à l'intérieur des pistes... on est en plein dans les bifurcations, mais autrement.
De Cenoman
(Publié le 23/05/2025)
@Robert, En voyant la grille 750 (version minimale), je me suis dit qu'il devait y avoir un truc que je ne voyais pas (du genre un automorphisme caché) et j'ai donné ma langue au chat... Je ne connais pas les Bp-braids. Quand vous affirmez qu'ils résoudraient la grille, est-ce une conviction ou est-ce une spéculation ?
De Cenoman
(Publié le 23/05/2025)
@Francis, Je suis entièrement d'accord avec Robert: les whips et les braids ne résolvent rien de plus que les pistes ou les chaînes et réseaux de chaînes. Mon solveur personnel (privé) n'a encore jamais failli à retrouver les mêmes éliminations. En référence aux échanges récents autour de la grille 745, et si vous voulez vous faire une idée de la comparaison entre les whips et les chaînes et réseaux de chaînes ("krakens" et multi-krakens), il existe un solveur public qui pourrait vous intéresser : YZF_Sudoku, écrit par un membre chinois (ysfwsf) du forum "The New Sudoku Players Forum" (forum.enjoysudoku.com), sous-forum Software. Le lien de téléchargement se trouve dans le premier message du fil. Ne pas se laisser impressionner par les messages éventuels de l'antivirus (c'est une programmation 'amateur', n'ayant pas tous les certificats officiels). L'aide n'est pas disponible en anglais, mais il est assez simple à utiliser, avec une interface du type hodoku.
De Jean
(Publié le 23/05/2025)
Les indications que vous donnez m'ont permis de résoudre la grille. J'aurais aimé trouvé une méthode de simplification. Dans la négative, j'ai exploré l'hypothèse d'un 8 en L1C2.Compte tenu de cette donnée supplémentaire, je suis arrivé au but en combinant les simplifications de base ( y compris le swordfish et l'exclusion) et, d'après mes notes, 6 fois la méthode des pistes.
De Alain
(Publié le 23/05/2025)
Bonjour Résolution manuelle de la grille initiale à partir de paires (sauf erreur de ma part) : Paire 89L6C9 : arbre de profondeur 2 validant 8L6C9 Paire 39L8C9 : arbre de profondeur 3 validant 9L8C9 Paire 8L17C3 : arbre de profondeur 2 validant 8L7C3 qui couvre la grille. Ouf !
De Francis Labetoulle
(Publié le 24/05/2025)
@Cenoman Bonjour et grand merci pour votre information sur l'existence d'un logiciel efficace de sudoku sur le forum enjoy sudoku, utilisant les "krakens" sur lesquels je dois m'initier... Cette grille 750 m'a été très instructive concernant la "méthodologie" des antipistes de Robert et son équivalence supposée avec les méthodes délicates de Denis Berthier traitées dans son livre : "Pattern-Based Constraint Satisfaction and Logic Puzzles", parlant après autres des Bp-braids, et que je n'ai pas encore eu le courage d'approfondir! Il me reste le plus délicat: faire le bon choix initial de ces antipistes!!! Bonne journée Francis
De Robert Mauriès
(Publié le 24/05/2025)
@ Cenoman : Bonsoir Bernard, Si j'ai bien compris la notion de Bp_Braids, je pense que la solution peut être apportée avec cet outil. NB : D'après François, cette grille que j'ai trouvée sur le site Top-Sudoku.com, est isomorphe à AI Escargot !
De Cenoman
(Publié le 25/05/2025)
@Robert C'est exact. Prenez AI Escargot (puzzle #23) Permutez les piles circulairement vers la gauche; échangez les bandes 1,3; échangez les lignes [1,2] [7,9]; permutez circulairement vers le bas les lignes [4,5,6] et vers la droite les colonnes [4,5,6]; échangez les chiffres [1->1] [2->5] [3->8] [4->9] [5->7] [6->3] [7->2] [8->6] [9->4] et vous obtenez le puzzle #750
De Robert Mauriès
(Publié le 25/05/2025)
@ Cenoman : Merci Bernard pour vos explications. Ainsi effectivement, se rapportant à l'AI Escargot, la résolution peut se faire avec des Bp_braids (B2_braids pour être précis) comme l'a expliqué Denis Berthier dans un fil de Enjoy Sudoku de 2012.
De Alain
(Publié le 26/05/2025)
Merci pour ces commentaires hautement techniques. Avec ma stratégie de pistes longues à partir de paires, j'ai dû faire 11 choix de paires à différents niveaux de profondeur. Je rapproche ce nombre du niveau TDP. Cela veut-il dire qu'on ne peut faire mieux ?
De Robert Mauriès
(Publié le 27/05/2025)
@ Alain : Bonjour Alain, Le niveau TDP de 11 est établit pour une profondeur de 3 maximum. Mais Francois C. a réduit à 10 le niveau TDP en allant à une profondeur de 5. Je doute qu'on puisse faire mieux.
Ajouter un commentaire
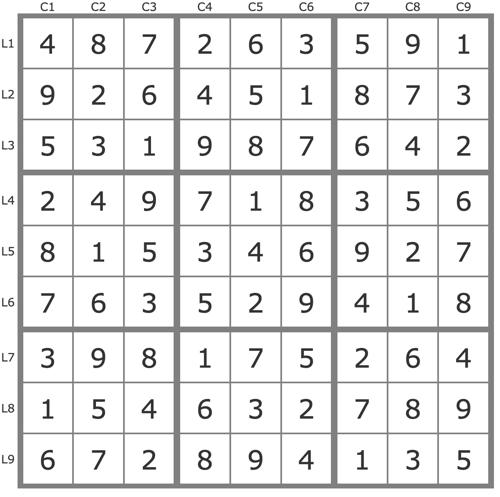
La solution
 En savoir plus ...
En savoir plus ...




