S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -747Cette grille très difficile de niveau 18 TDP présente une configuration dite de "Tridagon".
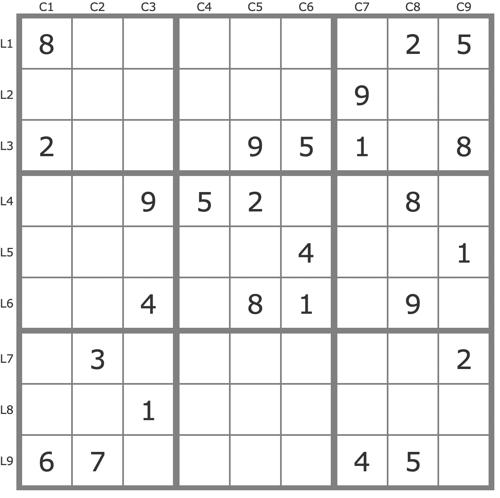
(*) grille proposée par "champagne" (c'est son pseudo) sur le site Enjoy Sudoku : http://forum.enjoysudoku.com/
Commentaires sur cette grille
De Robert Mauriès
(Publié le 12/05/2025)
Pas de commentaires pour l'instant, si ce n'est que pour en savoir plus sur le Tridagon, reportez-vous à ma résolution.
De Alain
(Publié le 21/05/2025)
Bonjour, Peu de commentaires sur cette grille déroutante! Peu de paires et beaucoup de "trios", ce qui gêne ma stratégie basée sur des bifurcations à partir de paires. J'arrive à résoudre, mais il me faut plonger à une profondeur de 4 (sous-sous-sous-piste), ce qui d'après Robert qui le tient de Denis Berthier, peut se réduire à 3. Pas simple!
De Robert Mauriès
(Publié le 21/05/2025)
@ Alain : Bonjour Alain, Il faut distinguer la profondeur d'un arbre de résolution de la profondeur de résolution d'une grille. Quand on dit que la profondeur de résolution d'une grille est de 3, donc T&E(3), cela veut dire que la résolution a été obtenue par des (1 ou plusieurs) arbres de résolution successifs de profondeur 3 maximum, dont un au moins est de profondeur 3, et non que la résolution a été obtenue avec un seul arbre de profondeur 3. Cette grille est bien de profondeur 3, cela se vérifie en montrant que l'arbre de résolution issue du 4L2C8 conduit à l'invalidité de toutes ses extrémités à la profondeur 3. Dès lors, après élimination du 4L2C8 qui en découle, la grille devient de profondeur 1.
De Alain
(Publié le 22/05/2025)
@ Robert Mauriès : Merci Robert. Oui, ma résolution utilise plusieurs arbres de résolution de profondeur max 4. Je suis parti du 8L9C3 qui me donnait de bonnes perspectives, mais j'ai eu besoin d'aller au 4e niveau. Comment mieux détecter la bonne paire initiale qui limitera la profondeur ? Je suis preneur de toute piste !
De Cenoman
(Publié le 23/05/2025)
Le Tridagon est une 'Configuration Impossible' (Impossible Pattern) de 12 cases, situées dans 4 blocs occupant exactement 2 piles et 2 bandes (forme globale de carré ou de rectangle) Les 12 cases contiennent trois mêmes chiffres (dans la grille 747, chiffres 3,6,7) occupant exactement 3 lignes et 3 colonnes à l'intérieur de chaque bloc (soit une diagonale, soit un triangle). Une condition importante de la démonstration d'impossibilité porte sur les orientations de ces figures dans les blocs : elles doivent être réparties 3+1, c.a.d. 3 orientations "diagonale principale" et 1 orientation "diagonale secondaire" ou l'inverse. Dans un bloc où les 3 cases sont en triangle, l'orientation est donnée par le petit coté du triangle isocèle. Grille 747 : on a trois orientations 'diagonale secondaire', blocs 2, 3, 5 et une orientation 'diagonale principale', bloc 6. La configuration est très facile à repérer sur la grille initiale, après les TB. C'est une configuration impossible, la grille n'aurait pas de solution si elle se retrouve telle quelle à la fin de la résolution. Pour que la grille ait une solution (au moins), il faut donc un (ou plusieurs) autre(s) candidat(s) dans une ou plusieurs des 12 cases (des gardiens). Ce n'est donc pas une technique d'unicité, au sens usuel du terme (que la grille ait une solution au plus). Autres configurations impossibles : l'oddagon, 5 candidats du même chiffre en conflit deux à deux (formant donc un polygone impair, d'où son nom en anglais), et avec la même configuration de cases, le 'bivalue oddagon', les cases étant occupées par des doublets. Denis Berthier et eleven ont cherché toutes les CI de trois chiffres dans 2 piles ou 2 bandes. Il en ont trouvé 630 ! Les puzzles avec tridagon sont le plus souvent très difficiles (cotation S.E. supérieure à 10 et souvent proche de 11.5). Pour ma part, il est déraisonnable de les résoudre sans recourir au fait qu'un gardien au moins doit être vrai. Ce recours ne résoud pas toujours le puzzle aussi facilement que dans l'exemple 747, retenu par Robert pour faire découvrir cette CI.
Ajouter un commentaire
La solution
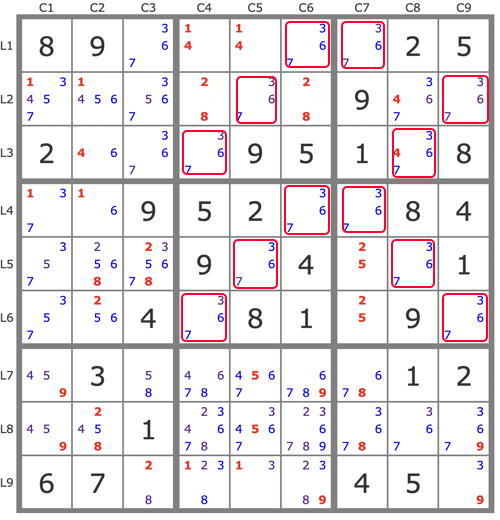
Après réduction de la grille par les TB, celle-ci présente une configuration dite de Tridagon représentée en rouge sur la figure suivante. Si le 4L3C8 n'était pas solution de sa case, cette configuration rendrait impossible l'existence d'une solution pour la grille. Donc L3C8=4.
La grille se termine alors en remarquant le X-wing(6L28C58) qui entraîne L6C9=6 et ensuite par inclusion,
Ou
(-6L6C9)->6L4C7->6L2C89->6L8C5->... => 6B9 vide => L6C9=6 et fin.
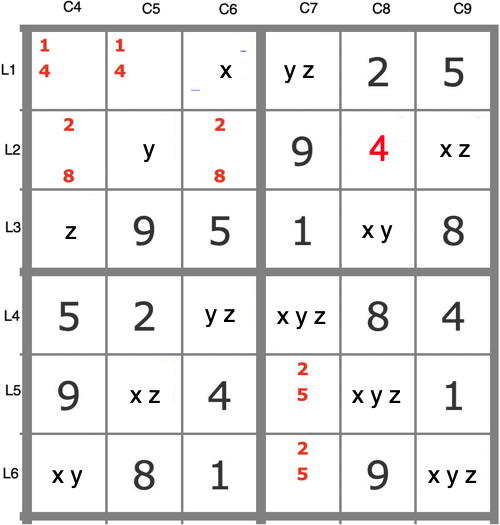
 Pour montrer que cette configuration des valeurs 367 dans les blocs 2,3,5,6 sans le 4L3C8 est impossible puisque la grille admet une solution, on désigne par x, y et z les valeurs que peuvent avoir les cases du bloc 2. Les cases des autres bloc 3, 5 et 6 prennent alors des valeurs fonctions de x, y ou z comme indiquées sur l'extrait de grille ci-dessous. Utilisons alors des anti-pistes pour conclure à l'impossibilité d'une solution.
(-zL1C7,-zL4C6)->[yL1C7->xL3C8->zL2C9 et yL4C6->xL6C4]->yL6C9->zL5C8->...
=> -zL4C7 => L4C7=xy
(-yL1C7,-yL4C6)->[zL1C7->xL2C9->yL3C8 et zL4C6->xL5C5->yL6C4]->zL6C9->yL5C8->... => -yL4C7 => L4C7=x
(-yL3C8)->xL3C8->zL2C9->yL6C9->... => -yL5C8 => L5C8=z =>L6C9=y => L6C4=x => L5C5 vide, donc pas de solution possible si L2C8=4.
Pour montrer que cette configuration des valeurs 367 dans les blocs 2,3,5,6 sans le 4L3C8 est impossible puisque la grille admet une solution, on désigne par x, y et z les valeurs que peuvent avoir les cases du bloc 2. Les cases des autres bloc 3, 5 et 6 prennent alors des valeurs fonctions de x, y ou z comme indiquées sur l'extrait de grille ci-dessous. Utilisons alors des anti-pistes pour conclure à l'impossibilité d'une solution.
(-zL1C7,-zL4C6)->[yL1C7->xL3C8->zL2C9 et yL4C6->xL6C4]->yL6C9->zL5C8->...
=> -zL4C7 => L4C7=xy
(-yL1C7,-yL4C6)->[zL1C7->xL2C9->yL3C8 et zL4C6->xL5C5->yL6C4]->zL6C9->yL5C8->... => -yL4C7 => L4C7=x
(-yL3C8)->xL3C8->zL2C9->yL6C9->... => -yL5C8 => L5C8=z =>L6C9=y => L6C4=x => L5C5 vide, donc pas de solution possible si L2C8=4.
 En savoir plus ...
En savoir plus ...




