S'identifier S'inscrire
assistant-sudoku.com
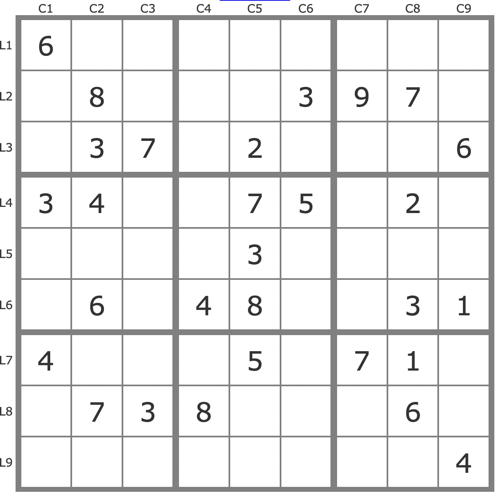
Grille Sudoku résolue
La grille -742Grille de niveau 3 TDP présentant quelques backdoors dont on tirera partie.
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 15/04/2025)
Bonjour Suivons les conseils de Robert (et mon cheminement empirique): Soit P'1 (-5L9C8) avec choix des bifurcations: P'11 = (6L2C4) et P'12 = (6L2C5). On vérifie que P'11 est invalide. P'12 "bifurque" en Q1 = (9L3C1) et Q2 = (9L8C1) toutes deux invalides. C'est donc bien un taille 3 puisque, comme prévisible, P1 = (5L9C8) remplit la grille.
De Philippe
(Publié le 15/04/2025)
Bonjour 5L8C1 couvre la grille Backdoor Unicité de la grille vérifié par 5L8C9 + 5L5C2 Invalide 5L8C9 + 5L5C3 + 1L1C2 Invalide 5L8C9 + 5L5C3 + 1L1C3 Invalide 5L8C9 + 5L5C3 + 1L2C1 Invalide 5L8C9 + 5L5C3 + 1L3C2 Invalide Bonne journée
De Jean
(Publié le 15/04/2025)
Grille résolue en utilisant Assistant Sudoku ( AS) ainsi que le logiciel ancien Sudoku3D (version1.1.1) utilisé pour vérifier la validité de la grille dans son état en cours ( 1 seule solution en vue) , recherche de simplifications de base jusqu'au X-Wing ( en manuel ou en guidé) . La résolution peut être décrite en 3 phases A/ Affichage de la grille détaillée AS pour validation des candidats isolés en rouge ; saisie dans Sudoku3D des valeurs déterminées sur AS ; Sudoku 3D ne propose pas de nouvelles simplifications B/ La situation ci-dessus est reproduite en colonne 1 sur l'image https://imgbox.com/EV5kYxTm ; Usage de AS pour le choix de 2 pistes : P1 partant de 6L2C4 et P2 de 6L2C5 . La piste 1 est invalide . Suppression de 6 L2C4 et validation piste 2 ; effacé piste 1 La colonne 2 intitulée Phase 1 reproduit AS dans le travail ci-dessus ( deux premières grilles) ; la troisième donne AS après les simplifications résultant de l'existence du triplent 149 dan le bloc 8 et de deux contradictions dans la grille ( qui justifient la suppression de 2 en L1C3 et 1 en L5C1) C/ Deuxième phases pour le choix d'un deuxièmz jeu de pistes (voir colonne 3 de l'image) . Choix de P1 en 6L4C7 et de P2 en 6L5C7 ; P2 invalide ; 6 validé en L4C7 et piste 2 effacé . Simplification grille en colonne 4 ( triplet 159) , candidat unique 7 en L1C4 puis en L9C6, triplet 149 , XWing de 8 en lignes 4 et 7, colonnes 3 et 9, . Les simplifications ci-dessus étant faites il est possible de terminer la partie sur Sudoku3D par la méthode des couleurs ( choix de 9 en L7C2) . AS confirme
De Robert Mauriès
(Publié le 15/04/2025)
@ Jean : Bonjour Jean et merci pour ces longues explications sur la manière dont vous avez résolu cette grille. Cette résolution me paraît compliquée néanmoins, mais présente des parties intéressantes comme l'apparition de triplets et d'un X-wing. En matière de logiciel, je vous conseille Hodoku (https://hodoku.sourceforge.net/en/index.php) Robert
De Robert Mauriès
(Publié le 15/04/2025)
@ Philippe : Bonjour Philippe, merci pour votre résolution. Une remarque cependant, vous n'avez pas besoin d'autant de bifurcations pour prouver que le 5L8C1 est la seule solution possible. En effet : - la piste (9L8C1) est directement invalide (sans bifurcation). - la piste (1L8C1) est invalide via les bifurcations (1L8C1).(8L5C1) et (1L8C1).(8L9C1). Ce qui justifie d'ailleurs que le niveau TDP est bien de 3.
De Philippe
(Publié le 15/04/2025)
@ Robert Mauriès : Merci Robert pour l info Il est vrai que j'ai assez galéré pour vérifier cette unicité mais j'ai fini par dompter cette grille (et ai pris du plaisir ce qui est important) Bonne journée
De François C.
(Publié le 15/04/2025)
Bonjour, voici une résolution avec 7 pistes invalides de longueur <= 9: Placements: 5L6C7, 2L8C7, 7L6C1, 7L5C9 PISTE: 9L5C2->2L6C3->9L6C6->9L4C9->5L8C9->2L2C9->2L1C2 => L7C2 vide => -9L5C2 PISTE: 9L5C1->8L9C1->3L9C7->3L1C9->2L2C9 => 2C1 vide => -9L5C1 Alignement: 9B4C3 => -9L1C3 -9L7C3 -9L9C3 PISTE: 9L7C6->9L1C5->9L3C1->9L8C9->8L4C9->3L7C9->3L9C4->7L9C6->2L7C4 => L7C2 vide => -9L7C6 PISTE: 2L7C2->6L7C6->8L7C3->8L5C1->2L2C1->2L1C9->3L1C7->3L9C4->2L9C6 => 7L9 vide => -2L7C2 Placements: 9L7C2, 9L3C1 Paires: 38B9p37 => -8L9C8 PISTE: 9L4C3->8L4C9->3L7C9->3L9C4->7L1C4->9L5C4 => 9L6 vide => -9L4C3 PISTE: 2L6C3->9L5C3->9L9C8->5L8C9->2L2C9->2L9C1->8L5C1->5L5C2->1L9C2 => L8C1 vide => -2L6C3 Placements: 9L6C3, 2L6C6, 6L7C6, 6L9C3, 6L2C5, 4L2C3 Paires: 15C4L23 => -1L1C4 -5L1C4 -1L4C4 -1L5C4 -1L9C4 Placements: 1L4C3, 1L5C6 Alignement: 8L4B6 => -8L5C7 -8L5C8 Alignement: 1C4B2 => -1L1C5 Alignement: 8C8B3 => -8L1C7 -8L1C9 -8L3C7 Alignement: 9B5C4 => -9L1C4 -9L9C4 Placements: 7L1C4, 7L9C6 PISTE: 8L9C1->3L9C7->3L1C9->2L2C9->2L5C1->5L5C2->5L9C8 => 5C9 vide => -8L9C1 Placements jusqu’à la fin.
De Robert Mauriès
(Publié le 16/04/2025)
@ François C. : Merci François pour cette résolution "pas à pas" optimale dès lors qu'on se limite à des enchaînements de longueur 9 maximum. J'ai reproduit votre résolution avec des anti-pistes, histoire de rechercher les ensembles générateurs conduisant aux mêmes enchaînements. Je donne ici cette version anti-pistes à l'intention de ceux qui voudraient comprendre comment choisir les ensembles générateurs. A noter aussi que l'on peut faire d'autres choix d'ensembles générateurs conduisant aux mêmes éliminations ou validations par des anti-pistes, mais avec des enchaînements différents. (-9L46C3)->2L6C3->9L6C6->9L4C9->5L8C9->2L2C9->2L9C1->9L7C2->... => -9L5C2 (-8L5C1)->8L9C1->3L9C7->3L1C9->2L2C9->2L5C1->... => -9L5C1 (et même -159L5C1) => -9L179C3 (-9L89C5,-9L8C6,-2L7C6)->9L1C5->9L3C1->9L8C9->8L4C9->3L7C9->3L9C4->7L9C6->2L7C4->9L7C2->... => -9L7C6 (-9L7C2)->2L7C2->6L7C6->8L7C3->8L5C1->2L2C1->2L1C9->3L1C7->3L9C4->2L9C6->... 7L9 vide => L7C2=9 => L3C1=9 et -8L9C8 (-9L4C9,-9L6C3)->8L4C9->3L7C9->3L9C4->7L1C4->9L45C4->... 9L6 vide => -9L4C3 (-9L6C3)->2L6C3->9L5C3->9L9C8->5L8C9->2L2C9->2L9C1->8L5C1->5L5C2->1L9C2->... => L8C1 vide => L6C3=9 + 9 placements et plusieurs éliminations par TB (-8L9C7,-25L9C1)->3L9C7->3L1C9->2L2C9->2L5C1->5L5C2->5L9C8->… 5C9 vide => -8L9C1 et fin On constate donc ici que les ensembles générateurs ne se réduisent pas toujours à un candidat. Comment sont-ils donc choisis ? L'idée est la suivante : on choisit un candidat (en général dans une paire) est on construit l'anti-piste issue de ce candidat. On sait que les candidats qui voient ce candidat générateur sont potentiellement "éliminables". Si l'anti-piste ne parvient pas à en éliminer un, on peut ajouter un autre (ou plusieurs) candidat(s) générateur(s) au premier afin de poursuivre le développement de l'anti-piste et arriver à ses fins. Evidemment, ces candidats générateurs ajoutés doivent impérativement voir au moins un des candidats qui voient le candidat générateur initial. Par exemple, pour la première des anti-pistes ci-dessus, en choisissant le 9L6C3 comme générateur on cible l'élimination des 9 qui le voient. Pour poursuivre le développement de l'anti-piste bloquée après le deuxième enchaînement on ajoute le 9L4C3 à l'ensemble générateur et on parvient alors à éliminer le 9L5C2. Autre exemple, pour la dernière anti-piste ci-dessus, on démarre avec le 8L9C7 comme élément générateur, mais on voit qu'on est bloqué après 3 enchaînements et qu'en ajoutant 25L9C1 on aboutit à un résultat. On rapprochera cette manière de faire de celle consistant à utiliser des bifurcations. Robert
De Alain
(Publié le 18/04/2025)
Pour moi aujourd'hui, pas de bifurcation. Paire 68L4C7, 8 invalide d'où 6L4C7 Paire 89L4C9, 9 invalide d'où 8L4C9 Paire 39L7C9, 9 invalide et le 3 couvre la grille avec l'unicité en prime !
Ajouter un commentaire
La solution
Simplification de la grille par les TB, puis élimination du 3L9C7 comme suit : (3L9C7).(2L9C1) invalide (3L9C7).(2L5C1).(6L7C3) invalide et (3L9C7).(2L5C1).(6L7C9) invalide. Donc validation du 8L9C7 et fin par induction (8L9C7 étant un backdoor). Ou alors résolution "pas à pas" réalisée au fil des observations... comme ceci par exemple, en exploitant notamment les doublets et alignements cachés. (-9L7C2)->2L7C2->27L9C46->3L7C4->3L1C9->2L2C9->2L5C1->8L9C1->8L7C9->... => -9L9C1, -9L7C4, -9L7C9 => -8L9C8 (-8L5C1)->8L9C1->3L9C7->3L1C9->2L2C9->2L5C1->... => -159L5C1 (-9L9C8)->9L8C9->[14L8C56 et 8L4C9->8L7C3->6L9C3]->9L9C5->... =>-9L9C2346 (-9L46C3)->2L6C3->9L6C6->9L4C9->5L8C9->2L2C9->2L9C1->9L7C2->... => -9L5C2 => -9L17C3 (-9L7C2)->9L7C6->9L1C5->... => -9L1C2 => L3C1=9 + 1 placement (-6L7C6)->2L7C6->9L6C6->9L89C5->9L1C4->7L9C4->3L7C4->... => -6L7C4 (-9L6C6)->2L6C6->23L79C4->7L1C4->9L45C4->... => -9L5C6 (-8L5C1)->8L9C1->3L9C7->3L1C9->2L2C9->2L5C1->... => -15L5C1 (-1L4C3)->1L4C4->26L57C6->2L6C3->8L5C1->... -8L4C3 => -8L5C78 => -8L13C7, -8L1C9 (-5L3C4)->5L3C8->[2L2C9 et 5L8C9->1L8C1]->5L2C1->... => -5L2C4 (-9L6C3)->9L6C6->9L89C5->9L1C4->[5L3C4 et 7L1C6->8L3C6]->4L3C8->9L5C8->... => -9L5C3 (-6L7C6)->6L7C3->8L7C9->9L4C9->9L6C3->2L6C6->... => -2L7C6 => L7C6=6 + 13 placements (-5L2C9)->5L2C1->5L8C9->... => -5L1C9 (ou X-wing sur 5C19) (-2L1C9)->3L1C9->8L7C9->2L7C3->… => -2L1C3 => L1C3=5 et fin
 En savoir plus ...
En savoir plus ...




