S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -737Une grille assez difficile dont le niveau TDP reste à établir, mais que l'on peux résoudre assez facilement "pas à pas" avec des jeux de pistes successifs.
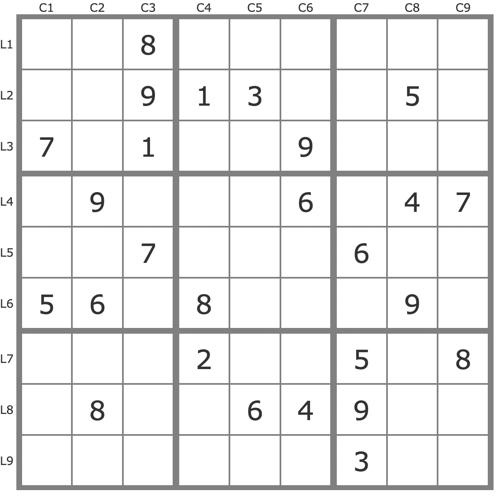
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 21/03/2025)
Bonjour Voici un taille 4 commençant par la case L8C4 possédant 3 chiffres ayant chacun un lien fort (propriété dont j'ai oublié le nom...) (5L8C4) : 0 (7L8C4) : 1. (3L4B4) :0 et 2. (3L5B4) : 0 (3L8C4) : 1. (3L6C9) :0 (Bien voir le triplet 148 de L5) 2. (-3L6C9) : 1
De Alain
(Publié le 21/03/2025)
Paire 4L67C3, piste 4L7C3 Sous-piste 3L8C4 invalide, valide la sous-piste 7L8C4 Sous-piste 1L9C2 invalide, sous-piste 2L9C2 invalide Valide 4L6C3 Paire 36L7C3, piste 3L7C3 Sous-piste 4L3C4 invalide, valide la sous-piste 6L3C4 Sous-piste 4L7C1 couvre la grille Excusez mon vocabulaire peu orthodoxe, mais que j'espère compréhensible ! Alain
De Robert Mauriès
(Publié le 21/03/2025)
@ Francis Labetoulle : Bonjour et bravo Francis pour cette résolution qui établit à 4 le niveau TDP de cette grille. Je crois qu'on ne peux pas faire mieux en matière de niveau TDP. La case L8C4 comportant 3 candidats faisant chacun partie d'une paire s'appelle un HUB.
De Robert Mauriès
(Publié le 23/03/2025)
@ Alain : Bonsoir Alain, J’ai vu et vérifié votre résolution de la grille 737. Le choix de la paire 4L67C3 confirme une fois de plus qu’une piste se développant bien (seule ou via des bifurcations) risque « fortement » de conduire à invalidité (Loi de Murphy), et du coup cela est beaucoup de travail pour ne placer au final qu’un seul candidat. C’est la raison pour laquelle je ne me suis pas intéressé à cette paire. Je vous invite à examiner la résolution très intéressante de Francis Labetoulle . Amicalement Robert
De Antoine Gillot
(Publié le 16/04/2025)
Bonjour, bon ben comme d'hab, c'est rock'n roll. piste 1 L6C9 bloquée donc bifurcation 4 et 9 de L5C4, le 4 est invalide donc on étudie le 9 qui nous laisse la piste 7 ou 5 de L9C4 à étudier. La piste 5 est invalide,la piste 7 nous laisse le 4 ou le 1 en L5C5, le 1 est invalide, le 4 termine la grille.
Ajouter un commentaire
La solution
Le niveau TDP d'une grille indique la difficulté de celle-ci. Il est donné par le nombre minimum de jeux de pistes nécessaires à la résolution de la grille.
Pour cette grille il reste à établir, préférant ici construire une résolution "pas à pas" avec des anti-pistes successives relativement courtes.
Petit rappel : l'anti-piste (-E) issue d'un ensemble de candidats E et la piste (E) issue de E forment un jeux de pistes conjuguées. En conséquence, si on développe (-E) alors un candidat qui voit à la fois un candidat de (-E) et tous les candidats de E peut être élimininé. Cela vaut évidemment si E n'est composé que d'un candidat.
C'est cette propriété qui est utilisée dans cette résolution pas à pas.
(-3L8C4,-5L8C3)->(3L7C6 et 5L9C3->6L7C3->4L6C3)->3L6C9->1L8C9->7L7C8->7L8C4->... => -5L8C4 => L8C3=5
(-6L7C8)->6L7C3->4L6C3->(49L5C45 et 3L4C3)->3L8C4->7L8C8->... => -7L7C8
(-6L7C8)->6L9C8->7L8C8->3L8C4->5L4C4->58L9C56->1L7C56->... -1L7C8 => L7C8=6 + 1 placement + éliminations 2p145B4
(-8L2C6)->7L2C6->7L6C5->4L6C3->3L7C3->3L8C4->3L4C1->8L4C7->... => -8L2C7 => L2C6=8 + 2 placements + éliminations par TB (voir paire 46L13C4)
(-5L4C4)->3L4C4->7L8C4->3L7C6->4L7C3->4L6C5->9L5C4->5L9C4->... => -5L13C4
(-2L6C7)->1L6C7->1L8C9->2L89C8->... => -2L5C8 => éliminations 2p289B5
(-1L4C5)->5L4C5->3L4C4->3L7C6->4L7C3->4L6C5->7L6C6->... => -1L6C56 => éliminations de 1p15B6
(-1L4C5)->5L4C5->5L9C4->5L1C6->2L5C6->... => -1L5C6 => -1L7C5
(-9L7C5)->(9L5C5->2L5C6 et 9L9C4->5L9C6)->7L1C6->7L6C5->... => -7L7C5 => L7C5=9 +3 placements.
(-5L9C6)->1L9C6->1L5C2->1L4C5->5L4C4->... -5L9C4 => L9C4=7 + 6 placements + éliminations par TB
(-8L3C8)->8L5C8->3L6C9->26L23C9->... => -2L3C8
(-8L4C7)->8L3C7->3L3C8->5L3C2->2L3C5->4L5C5->4L6C3->2L4C3->... => -2L4C7 => L4C7=8 et fin
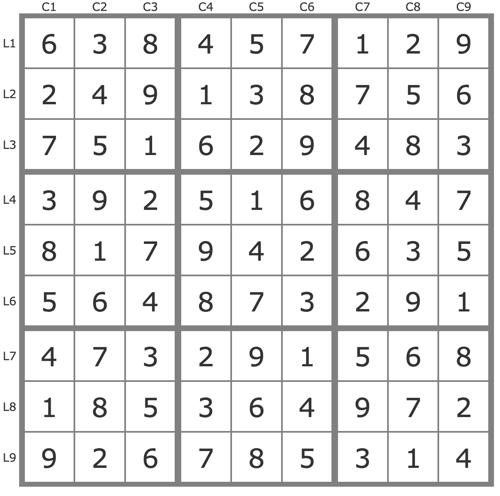
 En savoir plus ...
En savoir plus ...




