S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -730Cette grille présente une boucle permettant une première simplification, une occasion ici de présenter cette notion dans ma résolution.
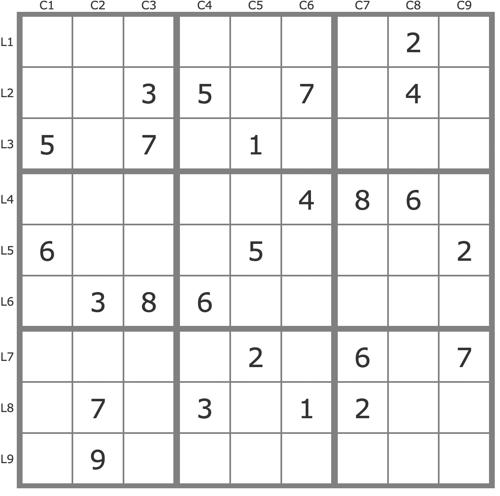
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 24/12/2024)
Voici une résolution de taille 3: P(2L6C1):0 P(4L6C1):0 puis avec les 3 de L4 : P(3L4C9):0 et P(3L4C5):1 bonnes fêtes
De Robert Mauriès
(Publié le 24/12/2024)
@ Francis Labetoulle : En effet, Francis, je ne trouve pas mieux qu'une résolution d'ordre 3 TDP. Cela dit, cette grille est l'occasion pour moi d'écrire sur de nouvelles notions : boucle, anti-piste interne à une piste, etc... ce que j'exposerai dans ma résolution. Bonne fête de noël à vous et votre famille.
Ajouter un commentaire
La solution
Cette grille est de niveau 3 TDP comme on peut le voir dans les commentaires du forum. 3 jeu de pistes suffisent donc à en venir à bout.
Cependant voici quelques notions applicables ici, histoire dans parler.
Définition :
Une piste (ou une antipiste) contient une boucle de candidats A1,A2,...,An lorsque, pour tout i, Ai->Ai+1 et An->A1
On peut alors établir le théorème suivant :
A1,A2,...,An étant une boucle d'une piste (ou une antipiste), si Bj est un candidat fortement lié à Aj (cad -Aj->Bj et -Bj->Aj), alors, tout candidat Cj qui voit à la fois Bj et un candidat Ai≠Aj peut être éliminé.
Pour la grille 730 proposée ici, après simplification par les TB on voit que la piste P(4L5C2):4L5C2->4L3C4->2L4C4->1L5C4->8L5C6->3L4C5->... contient la boucle 4L5C2, 4L3C4, 2L4C4, 1L5C4.
On peut donc supprimer 9 candidats (barrés sur la grille ci-dessous).
En effet, par exemple, le 4L1C2 et le 4L7C2 voient le 4L5C2 et le 4L3C2 qui est fortement lié au 4L3C4. Le 7 et le 9 de L4C4 voient le 2L4C4 et le 1L4C4 qui est fortement lié au 1L5C4, etc...
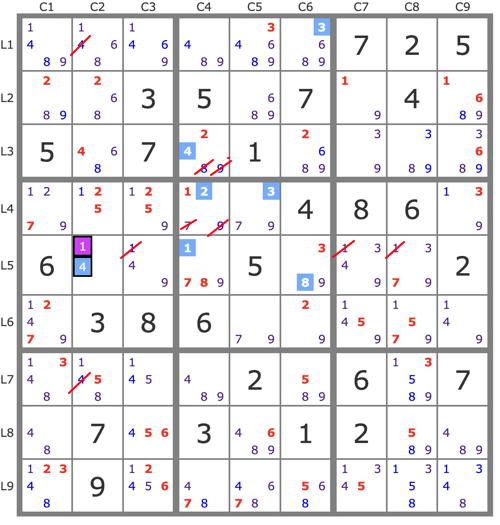 Dès lors, l'anti-piste suivante permet 5 placements, à savoir :
(-1L5C2)=>1L5C4->8L5C6->3L4C5->7L6C5->9L6C6->5L7C6->56L89C3->2L9C1->... => 2L6 vide => -1L5C4 => 5 placements.
La grille alors simplifiée par ces placements est la suivante que l'on va résoudre en utilisant la notion d'antipiste interne (ou secondaire).
Définition :
Une antipiste P'(B) (ou une piste P(B)) : B1->B2->... ->Bp->... est une antipiste (ou une piste) interne d'une antipiste P'(A) : (-A)->A1->A2->... ->An->... lorsque les candidats Bi sont placer en tenant compte du placement de tous les candidats Aj.
Cette définition est à rapprocher de celle d'une P-Piste décrite dans la théorie des pistes 1 ou 2 ci-contre.
On peut alors établir les théorèmes suivants :
Th1
Soit P'(B) une antipiste interne d'une antipiste P'(A) :
- si un candidat C voit à la fois B et un candidat de P'(B), C n'est pas un candidat de P'(A) et l'antipiste interne P'(C) prolonge P'(A).
- si P'(B) conduit à une impossibilité, B est un candidat de P'(A) et la piste interne P(B) prolonge P'(A)
Th2
Soit P'(B) une antipiste interne d'une antipiste P'(A), si les conditions du théorème 1 sont remplies, alors :
- si l'antipiste prolongée conduit à une impossibilité, A est solution de sa case.
- si un candidat D voit à la fois A et un candidat de l'antipiste prolongée, D peut être éliminé de sa case.
Dans le cas de cette grille :
A=2L2C2 soit (-2L2C2)=>2L4C2->5L7C2->5L9C6->5L8C8->5L6C7->...
B=9L2C5 soit (-9L2C5)->68L2C25->6L3C9->6L1C6->3L1C5->79L46C5->... => 9L8C5 n'est pas un candidat de P'(A), c'est donc 9L8C9 et P(9L8C9) qui prolongent P'(A) et rencontre une impossibilité dans B3.
Nous pouvons écrire cet enchainement comme ceci :
(-2L2C2)=>2L4C2->5L7C2->5L9C6->5L8C8->5L6C7->[(-9L2C5)->68L2C25->6L3C9->6L1C6->3L1C5->79L46C5->... => -9L8C5]->9L8C9->3L4C9->79L46C5->9L2C7->1L2C9->1L6C8->38L79C8->... 8B3 vide => L2C2=2 et fin.
P'(A) est tracée en bleue, P'(B) est tracée en jaune, le prolongement de P'(A) en vert.
Dès lors, l'anti-piste suivante permet 5 placements, à savoir :
(-1L5C2)=>1L5C4->8L5C6->3L4C5->7L6C5->9L6C6->5L7C6->56L89C3->2L9C1->... => 2L6 vide => -1L5C4 => 5 placements.
La grille alors simplifiée par ces placements est la suivante que l'on va résoudre en utilisant la notion d'antipiste interne (ou secondaire).
Définition :
Une antipiste P'(B) (ou une piste P(B)) : B1->B2->... ->Bp->... est une antipiste (ou une piste) interne d'une antipiste P'(A) : (-A)->A1->A2->... ->An->... lorsque les candidats Bi sont placer en tenant compte du placement de tous les candidats Aj.
Cette définition est à rapprocher de celle d'une P-Piste décrite dans la théorie des pistes 1 ou 2 ci-contre.
On peut alors établir les théorèmes suivants :
Th1
Soit P'(B) une antipiste interne d'une antipiste P'(A) :
- si un candidat C voit à la fois B et un candidat de P'(B), C n'est pas un candidat de P'(A) et l'antipiste interne P'(C) prolonge P'(A).
- si P'(B) conduit à une impossibilité, B est un candidat de P'(A) et la piste interne P(B) prolonge P'(A)
Th2
Soit P'(B) une antipiste interne d'une antipiste P'(A), si les conditions du théorème 1 sont remplies, alors :
- si l'antipiste prolongée conduit à une impossibilité, A est solution de sa case.
- si un candidat D voit à la fois A et un candidat de l'antipiste prolongée, D peut être éliminé de sa case.
Dans le cas de cette grille :
A=2L2C2 soit (-2L2C2)=>2L4C2->5L7C2->5L9C6->5L8C8->5L6C7->...
B=9L2C5 soit (-9L2C5)->68L2C25->6L3C9->6L1C6->3L1C5->79L46C5->... => 9L8C5 n'est pas un candidat de P'(A), c'est donc 9L8C9 et P(9L8C9) qui prolongent P'(A) et rencontre une impossibilité dans B3.
Nous pouvons écrire cet enchainement comme ceci :
(-2L2C2)=>2L4C2->5L7C2->5L9C6->5L8C8->5L6C7->[(-9L2C5)->68L2C25->6L3C9->6L1C6->3L1C5->79L46C5->... => -9L8C5]->9L8C9->3L4C9->79L46C5->9L2C7->1L2C9->1L6C8->38L79C8->... 8B3 vide => L2C2=2 et fin.
P'(A) est tracée en bleue, P'(B) est tracée en jaune, le prolongement de P'(A) en vert.
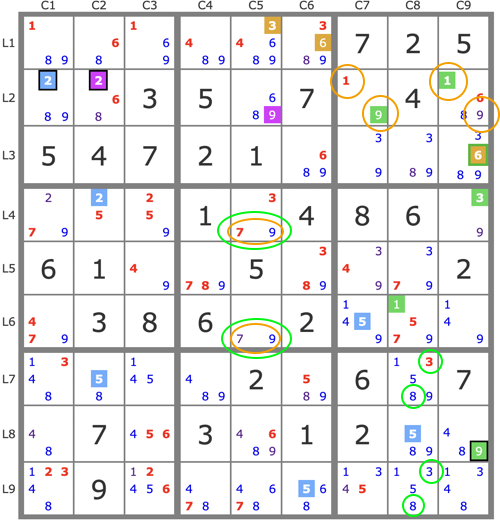 On trouvera sur le site New Sudoku Palyer's Forum une autre présentation de cette résolution
On trouvera sur le site New Sudoku Palyer's Forum une autre présentation de cette résolution
 En savoir plus ...
En savoir plus ...




