assistant-sudoku.com

Grille Sudoku résolue

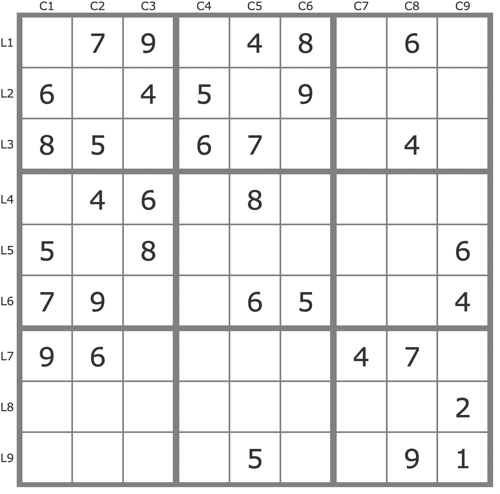
La grille -726
Cette grille très difficile laisse apparaître un "tridagon", une configuration impossible si certains candidats étaient éliminés, candidats que l'on appelle des "gardiens".
L'utilisation des gardiens simplifie la résolution.
Cette grille est proposée par Coloin sur le site New Sudoku Player's Forum ( http://forum.enjoysudoku.com/mission-impossible-t45243.html ) où vous trouverez différentes résolutions en plus de celle que je propose ici.

Afficher les commentaires Cacher les commentaires

---

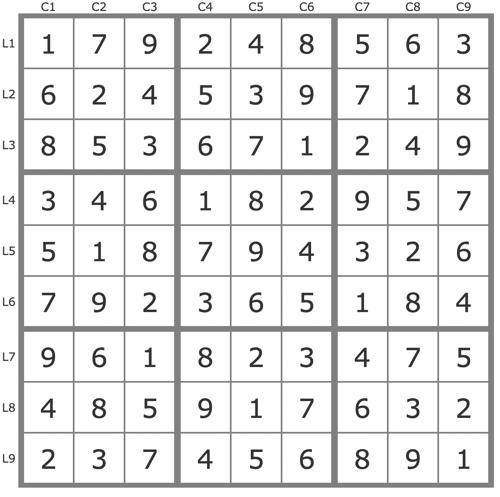
La solution

Trd = Tridagon 123p159B124,p357B5 est une configuration impossible si elle apparaissait, à savoir que la grille n'aurait alors pas de solution. Cela se vérifie en montrant que tous les choix possibles des valeurs 1,2 et 3 de la configuration conduisent à contradiction si les deux gardiens sont éliminés en même temps. Les gardiens sont ici le 9L5C5 et le 7L4C6. Dès lors, voici une résolution en quelques étapes courtes avec des antipistes. (-9L5C5 & Trd)=>7L4C6->7L5C7->... => -9L5C7 (-7L4C9)=>7L2C9->8L7C9->(123L167C4 et 123L7C456->9L8C5->9L5C4)->7L4C4->... => -7L4C6 (-9L5C5)=> Trd => L5C5=9 +TB (-1L1C1)=>1L4C1->1L6C4->1L1C7->5L1C9->5L7C3->1L8C2->... => -1L2C2 et -1L1C4 (-2L13C7)=>2L2C8->1L2C5->1L8C2->8L8C8->8L6C7->2L5C7->3L5C2->... L2C2 vide => -2L2C8, -2L56C7 (-1L13C7, -1L5C2)=>(1L1C1->1L2C8 et 1L8C2->3L8C5)->2L2C5->3L2C2->2L5C2->3L4C1->3L3C6->... -1L5B7 => L5C7=3 (-1L5B2)=>1L5C8->3L2C8->2L2C2->... => -2L5B2 et fin