S'identifier S'inscrire
assistant-sudoku.com
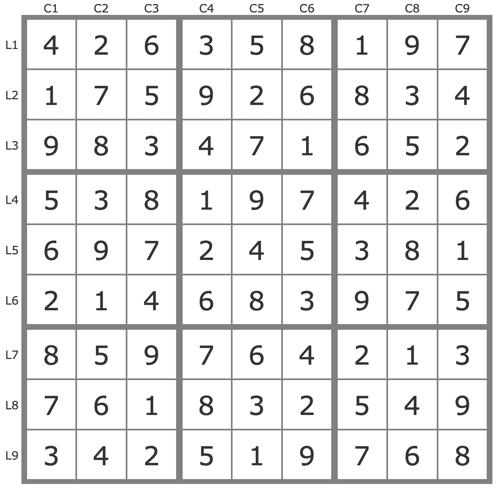
Grille Sudoku résolue
La grille -697Grille de niveau 4 TDP
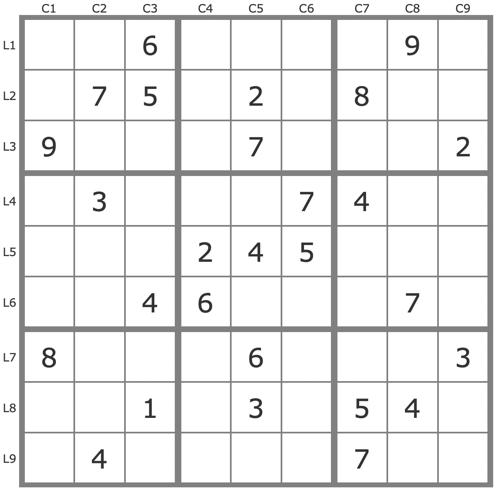
Commentaires sur cette grille
De Robert Mauriès
(Publié le 20/01/2022)
Résolution pas à pas avec la TDP en cliquant sur "Voir la résolution".
De Francis Labetoulle
(Publié le 21/01/2022)
Bonjour Grille qui m'a posé problème car il m'a fallu quelques essais pour choisir finalement la case L1C7, bien que d'autres choix semblaient également envisageables. À analyser.... Voici mon cheminement : P(3L1C7).P(1L2C1) : 0; P(3L1C7).P(3L2C1) : 0; P(1L1C7).P(3L2C1): 0; P(1L1C7).P(1L2C1) : 1, avec xwing des 8, ou encore skyscraper aisé à déceler. J'aurais pu également partir de la case L2C8, avec (6L2C8) et son antipiste, pour un cheminement similaire.
De Robert Mauriès
(Publié le 23/01/2022)
@ Francis Labetoulle : Bonjour Francis. En fait cette grille est de niveau 3 TDP comme l'a montré François sur le forum New Sudoku Players' où nous participons. Il utilise les whips de Berthier, mais sa résolution peut être la suivante en termes de pistes : - P(1L2C8) invalide, puis - P(3L2C1) invalide, puis - P(5L4C9) invalide => solution. Robert
De Francis Labetoulle
(Publié le 23/01/2022)
Bonsoir Robert Merci pour cette information. Elle me suggère une question de fond . Peut-on vraiment envisager une résolution à base de whips et de braids sans un logiciel approprié, dans un laps de temps acceptable? Si oui je m'investirai dans une telle voie!
De Robert Mauriès
(Publié le 24/01/2022)
@ Francis Labetoulle : Bonjour Francis, La réponse à votre question est Non à mon avis. Manuellement il faut du temps, comme il en faut aussi pour faire des résolutions "pas à pas" comme je les propose avec des ant-pistes. Berthier et François (je crois) utilisent un logiciel. Les modèles de Berthier (whip, bread etc...) n'apportent rien de plus en matière de résolution pratique, ils constituent cependant une belle théorie pour les "fondus" de logique mathématique. Robert
Ajouter un commentaire
La solution
Après simplification de la grille par les TB (6 placements et 2 éliminations), on utilise la Technique des Pistes avec des jeux de piste-antipiste successifs. On ne développe que l'antipiste P' (verte), la piste P (violette) étant réduite à un candidat.
P'(1L1C7) : -1L13C7 => [ (1L2C8 et 3L1C7)->3L2C1 ]->3L3C4-> (4L7C4->7L7C3 et 8L3C3)->9L5C3->29L67C7 … => -1L67C7 => -9L5C7
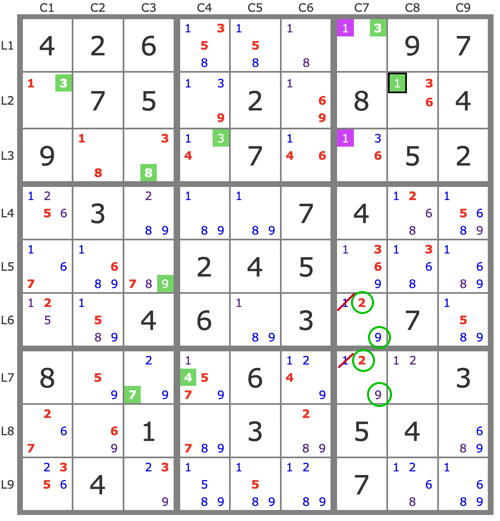 P'(5L7C2) : -5L7C2 => [ 5L7C4->7L7C3 et 5L9C1->3L9C3 ]->2L8C1->2L6C7->9L7C7 ... => -9L7C2 => L7C2=5
P'(5L7C2) : -5L7C2 => [ 5L7C4->7L7C3 et 5L9C1->3L9C3 ]->2L8C1->2L6C7->9L7C7 ... => -9L7C2 => L7C2=5
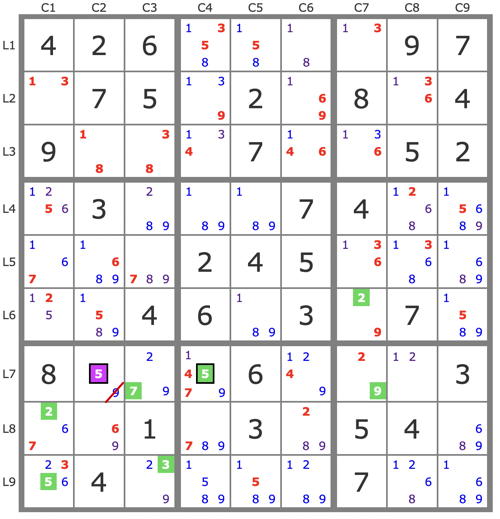 P'(9L2C4) : -9L2C4 => 9L2C6->6L3C6->6L5C7->(6L4C1->5L6C1)->(2L4C3->2L6C7->9L7C7)->7L7C3->7L8C4 ... => -9L78C4.
P'(9L2C4) : -9L2C4 => 9L2C6->6L3C6->6L5C7->(6L4C1->5L6C1)->(2L4C3->2L6C7->9L7C7)->7L7C3->7L8C4 ... => -9L78C4.
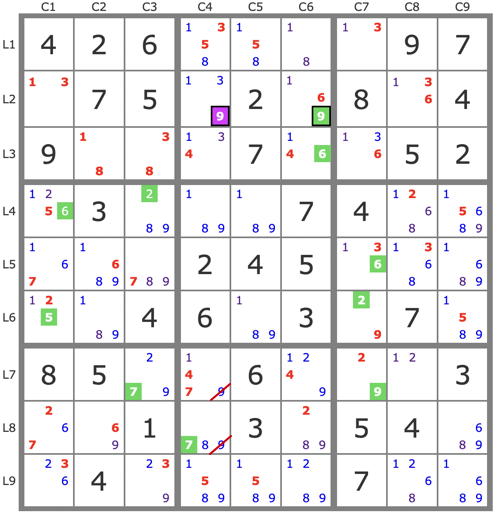 P'(6L2C6) : -6L2C6 => 6L3C6->6L5C7->6L4C1->(5L6C1->2L6C7->9L7C7 et 6L8C2)->9L8C6 => -9L2C6 => L2C4=9
P'(6L2C6) : -6L2C6 => 6L3C6->6L5C7->6L4C1->(5L6C1->2L6C7->9L7C7 et 6L8C2)->9L8C6 => -9L2C6 => L2C4=9
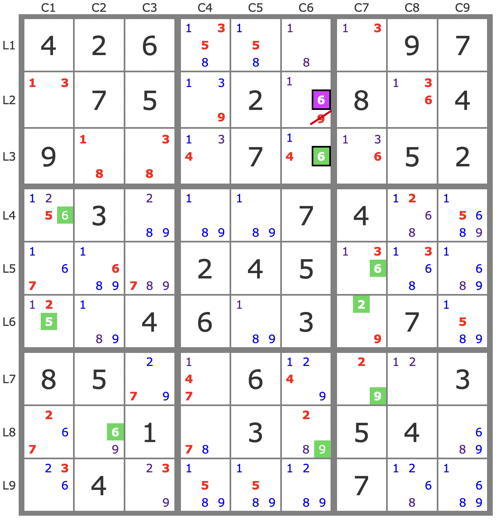 P'(6L3C7) : -6L3C7 => 6L3C6->4L3C4->3L1C4->1L1C7 => -1L3C7
P'(6L3C7) : -6L3C7 => 6L3C6->4L3C4->3L1C4->1L1C7 => -1L3C7
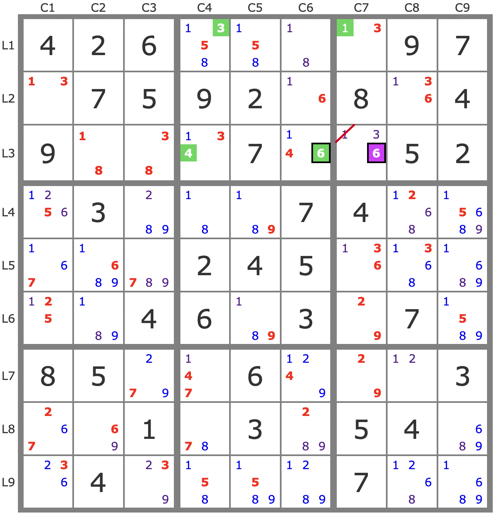 P'(6L3C7) : -6L3C7 => 6L5C7->6L4C1->(5L6C1->2L6C7->9L7C7 et 6L8C2)->9L9C3->3L3C3 => -3L3C7 => L3C7=6, L2C6=6.
P'(6L3C7) : -6L3C7 => 6L5C7->6L4C1->(5L6C1->2L6C7->9L7C7 et 6L8C2)->9L9C3->3L3C3 => -3L3C7 => L3C7=6, L2C6=6.
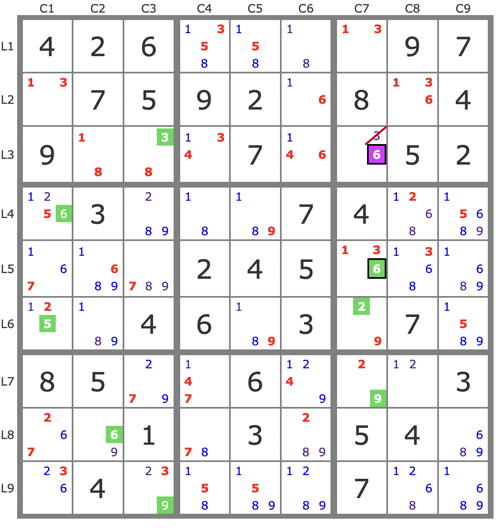 P'(8L3C2) : -8L3C2 => 1L3C2->(3L2C1 et 4L3C6->4L7C4->7L7C3)->26L89C1->6L5C2 => -8L5C2
P'(8L3C2) : -8L3C2 => 1L3C2->(3L2C1 et 4L3C6->4L7C4->7L7C3)->26L89C1->6L5C2 => -8L5C2
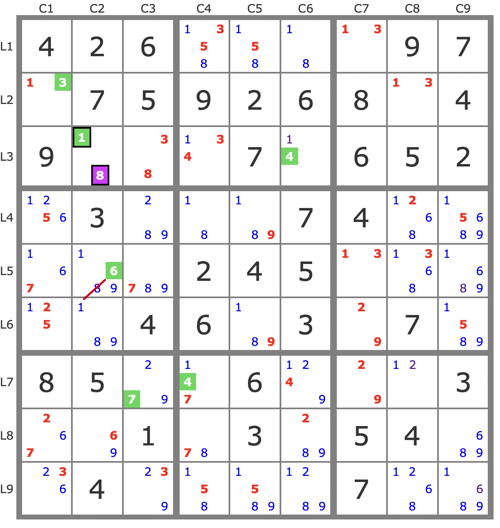 P'(1L1C7) : -1L7C1 => 1L2C8->( 2L7C8->9L7C7 et 3L2C1->3L3C4->4L7C4 )->1L7C6 => -1L1C6 => L1C6=8.
P'(1L1C7) : -1L7C1 => 1L2C8->( 2L7C8->9L7C7 et 3L2C1->3L3C4->4L7C4 )->1L7C6 => -1L1C6 => L1C6=8.
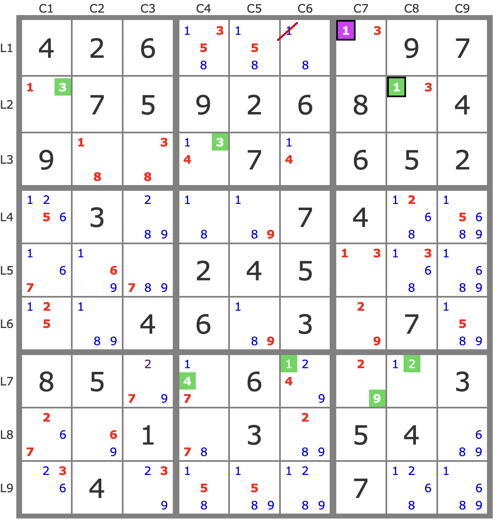 P'(3L2C8) : -3L2C8 => 3L1C7->3L3C4->( 8L3C3 et 4L7C4->7L8C4->8L8C9 )->8L5C8 => -3L5C8 => L2C8=3 et 9 placements par induction (candidats uniques).
P'(3L2C8) : -3L2C8 => 3L1C7->3L3C4->( 8L3C3 et 4L7C4->7L8C4->8L8C9 )->8L5C8 => -3L5C8 => L2C8=3 et 9 placements par induction (candidats uniques).
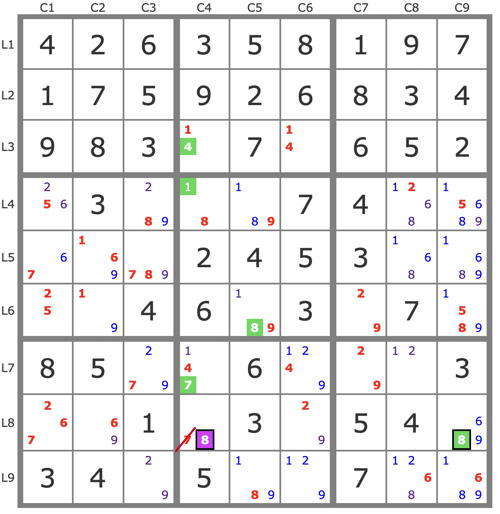
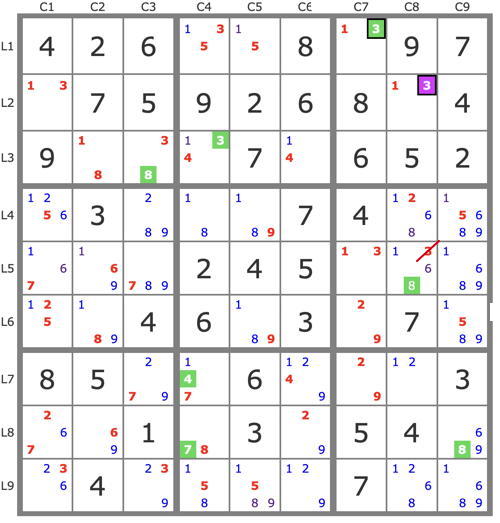 P'(8L8C4) : -8L8C4 => 8L8C9->8L6C5->(1L4C4->4L3C4)->7L7C4 => -7L8C4 => 8L8C4 et fin de la grille.
P'(8L8C4) : -8L8C4 => 8L8C9->8L6C5->(1L4C4->4L3C4)->7L7C4 => -7L8C4 => 8L8C4 et fin de la grille.
 En savoir plus ...
En savoir plus ...




