S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -691Grille de niveau 14 conventionnel.
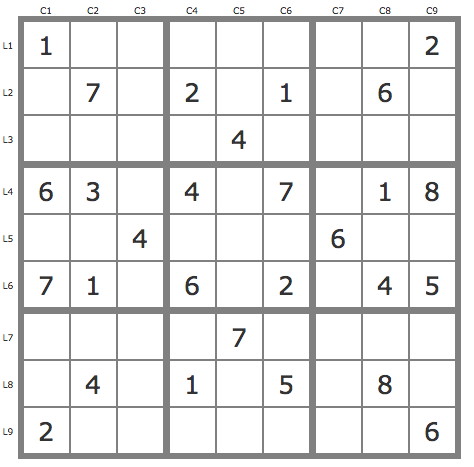
Commentaires sur cette grille
De François C.
(Publié le 10/02/2021)
Bonjour, Grille de niveau TDP <= 4 Voici une résolution avec 4 pistes invalides de 10 candidats maximum : Candidats uniques: 4L1C7, 4L2C1, 1L5C5, 4L9C6, 4L7C9, 2L8C5, 6L8C3, 6L7C6, 6L3C2, 6L1C5, 2L3C3, 2L4C7, 2L5C2, 2L7C8, 7L9C3, 1L9C7, 1L3C9, 1L7C3 Alignement: 3C3B1 => -3L3C1 P(3L2C5) = 3L2C5,9L2C9,3L6C7,3L8C9,9L8C1,3L9C4,9L5C8,9L9C5, => 9B5 vide => -3L2C5 P(8L2C5) = 8L2C5,5L4C5,5L5C1,8L3C7,9L3C1,7L8C7,9L8C9,9L2C7,3L6C7,3L9C5, => 3B9 vide => -8L2C5 Paire nue: 59C5L24 => -9L6C5 -9L9C5 Alignement: 9B8C4 => -9L1C4 -9L3C4 -9L5C4 P(8L5C1) = 8L5C1,9L6C3,3L6C7,3L9C5,3L7C1,5L3C1,5L5C4,5L1C8,7L1C4,3L3C4, => 3C8 vide => -8L5C1 Candidats uniques: 8L6C3, 3L6C5, 9L6C7, 8L9C5, 8L2C7 Alignement: 3C6B2 => -3L1C4 -3L3C4 P(9L2C5) = 9L2C5,3L2C9,5L2C3,3L1C3,8L1C6,9L1C2,9L3C8,9L9C4,3L9C8, => 3C7 vide => -9L2C5 Candidats uniques jusqu’à la solution.
De François C.
(Publié le 10/02/2021)
Autre résolution : avec 10 pistes invalides de 4 candidats maximum : Candidats uniques: 4L1C7, 4L2C1, 1L5C5, 4L9C6, 4L7C9, 2L8C5, 6L8C3, 6L7C6, 6L3C2, 6L1C5, 2L3C3, 2L4C7, 2L5C2, 2L7C8, 7L9C3, 1L9C7, 1L3C9, 1L7C3 Alignement: 3C3B1 => -3L3C1 1) P(9L9C5) = 9L9C5,9L4C3,9L6C7,9L2C9, => 9C8 vide => -9L9C5 Alignement: 9B8C4 => -9L1C4 -9L3C4 -9L5C4 2) P(9L5C9) = 9L5C9,3L2C9,3L6C7,3L9C5, => 3C8 vide => -9L5C9 3) P(9L8C7) = 9L8C7,3L6C7,7L5C9, => 7L8 vide => -9L8C7 4) P(9L9C8) = 9L9C8,9L8C1,9L5C6,9L3C7, => 9C9 vide => -9L9C8 5) P(3L8C7) = 3L8C7,9L6C7,5L7C7, => L9C8 vide => -3L8C7 Candidats uniques: 7L8C7, 7L5C9 6) P(3L9C8) = 3L9C8,3L2C9,3L6C5, => 3L5 vide => -3L9C8 Candidat unique: 5L9C8 Alignement: 3L9B8 => -3L7C4 Paire nue: 39C7L67 => -3L2C7 -9L2C7 -3L3C7 -9L3C7 7) P(5L3C1) = 5L3C1,5L1C4, => 5L5 vide => -5L3C1 8) P(8L6C5) = 8L6C5,8L5C1,3L6C7,3L7C1, => 5C1 vide => -8L6C5 Candidat unique: 8L6C3 9) P(8L9C2) = 8L9C2,8L2C5, => 8L1 vide => -8L9C2 Candidats uniques: 9L9C2, 3L8C1, 9L8C9, 3L2C9, 3L7C7, 9L6C7, 3L5C8, 3L6C5, 8L9C5, 9L7C4, 3L9C4, 8L2C7, 5L3C7, 3L3C6, 3L1C3 10) P(5L7C2) = 5L7C2,8L1C2,9L1C6,5L2C5, => 5L1 vide => -5L7C2 Candidats uniques jusqu’à la solution.
De Francis Labetoulle
(Publié le 03/06/2021)
Bonjour à tous Je propose une résolution selon la technique des pistes, à la JC. La case L5C1 semble la plus prometteuse, les 3 pistes pouvant se développer. De fait, P9L5C1 couvre la grille. On peut poursuivre avec les deux autres candidats. Il est plus ludique de vérifier que P'. P(3L6C5) et P'.P(3L6C7) sont toutes deux invalides, P' désignant l'antipiste de P9L5C1. Pour celà on utilisera avec modération des xwings à la JC et des Nishiotemplates checks du 3 ou 9 de la case L9C8 selon le cas.
De Robert
(Publié le 07/06/2021)
@ Francis Labetoulle : Bonjour Francis. Pouvez-vous expliquer ce que sont des "Nishiotemplates checks" ou proposer une référence permettant de se documenter. Merci à vous.
De Francis Labetoulle
(Publié le 08/06/2021)
@ Robert : Bonjour Robert Bien content de pouvoir échanger quelques commentaires après cette longue période. Le terme Nishio/template Check est utilisé parfois. D'après les exemples que j'ai étudiés, j'ai interprèté celà comme un cas d'invalidité associé à la disparition de tous les candidats d'une occurrence donnée dans une zone. En fait, en supposant un candidat valide on constate que cette hypothèse entraîne, dans les cas usuels, que tous les candidats de même occurrence d'un bloc disparaissent. Rien de bien nouveau dans celà, mais l'intérêt de cette méthode vient de la facilité de la détection "graphique" de tels candidats, au même titre que les xwings généralisés, avec un peu d'entraînement. Les cas cités dans mon commentaire sont vraiment des cas d'école. Comme j'ai quelques réserves à m'investir des les dernières méthodes proposées par Denis Berthier, je préfère m'en tenir à une approche plus "visuelle", voire quasi systématique : choix judicieux de pistes conjuguées et méthodes graphiquement aisées en plus des TB : xwing, etc, en complétant progressivement la panoplie. Bonne journée
De Didier Griffaut
(Publié le 14/12/2021)
Bonjour, Après les TB, les pistes successives: 9L4C5 puis 9L5C1 développent la grille. Est-ce un niveau TDP <= 2 ? Bonne suite
De Didier Griffaut
(Publié le 15/12/2021)
En effet, je n'avais pas bien lu le commentaire de Francis Labetoulle, 9L5C1 suffit à couvrir la grille. Les deux autres candidats donnant des pistes invalides. "La case L5C1 semble la plus prometteuse, les 3 pistes pouvant se développer." D'où ma question: existe-t-il une stratégie permettant de sélectionner le meilleur candidat d'une grille ? autrement que par le "feeling" ou le tâtonnement et autre pifométrie.
De Robert Mauriès
(Publié le 25/12/2021)
@ Didier Griffaut : Bonjour Didier, Pour répondre à votre question "existe-t-il une stratégie permettant de sélectionner le meilleur candidat d'une grille ?", voici ce que je peux vous dire. Disons d'abord qu'il n'y a pas de stratégie miracle qui marche à tout les coup, que ce soit d'ailleurs avec les méthodes traditionnelles ou avec la Technique des Pistes. Avec les méthodes traditionnelles, il faut repérer les schémas qui permettent de faire des éliminations (X-wing, Swordfish, etc...). Pour la technique des pistes, il en va de même mais différemment, il faut repérer les paires de candidats et les paires d'ensembles de candidats qui conduisent à des éliminations. Parmi celles-ci il faut privilégier d'abord les paires dont une des deux pistes conjuguées se développe bien car celle-ci conduira, généralement mais pas toujours, à des éliminations par croisement avec l'autre piste ou à invalidité. Dès qu'une nouvelle paire apparaît après des éliminations, il faut s'y intéresser. Il faut aussi s'intéresser aux paires couplées avec d'autre paires, c'est à dire des paires ayant une case ou un bloc en commun. Voici quelques éléments qui vous guideront pour ne pas trop tâtonner. Cordialement Robert
Ajouter un commentaire
La solution
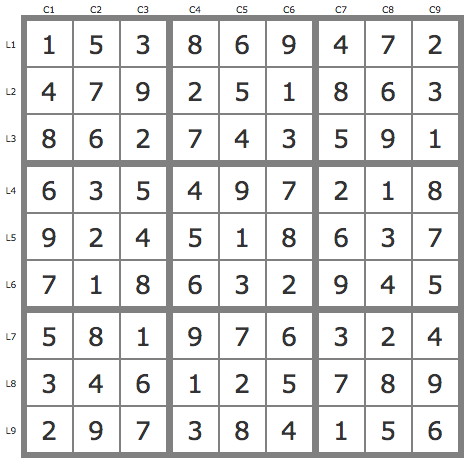
 En savoir plus ...
En savoir plus ...




