S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -690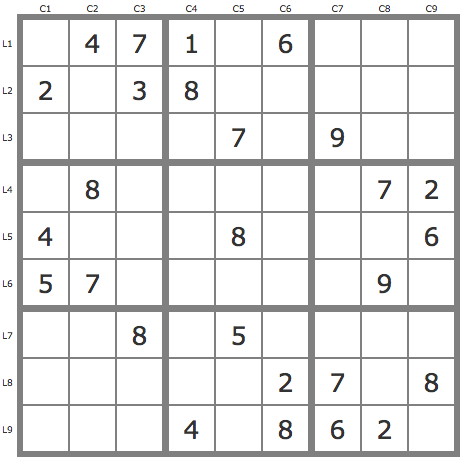
Commentaires sur cette grille
De Robert Mauriès
(Publié le 17/01/2021)
Pas de commentaire pour l'instant.
De Paolo
(Publié le 17/01/2021)
1) 9 placements par les TB initiales. P(1L3C9) =>couvre la grille 2) P(4L3C9).P(3L1C9)=>invalide 3) P(4L3C9).P(5L1C9)=>invalide =>-4L3C9 4) P(3L3C9)=>invalide=>solution.
De François C.
(Publié le 19/01/2021)
Candidats uniques: 7L2C9, 2L3C4, 2L1C7, 8L6C7, 2L7C2, 2L5C3, 2L6C5, 7L9C1, 4L8C3 Alignement: 5L1B3 => -5L2C7 -5L2C8 -5L3C8 -5L3C9 Alignement: 5C4B5 => -5L4C6 -5L5C6 Alignement: 5C7B6 => -5L5C8 Ensuite avec 3 pistes invalides relativement courtes : P(3L3C9) : 3L3C9,5L1C9,3L1C5,3L9C2,5L9C3,9L4C3,1L5C2,3L5C8,3L8C4,6L6C4 => L6C3 vide => -3L3C9 Paire 14B3p49 => -1L2C8 -4L2C8 -1L3C8 -4L3C8 Candidats uniques: 6L2C8, 4L7C8 P(3L1C9) : 3L1C9,9L1C5,3L3C6,4L3C9,1L6C9,9L7C9,9L8C4,9L4C1,3L5C2 => L5C8 vide => -3L1C9 Candidats uniques: 5L1C9, 5L8C8, 1L5C8 P(3L6C9) : 3L6C9,6L6C4,6L7C1,6L4C3,9L9C3,1L9C9,1L7C6,3L9C5,9L1C5,9L4C1,9L5C6 => 7C6 vide => -3L6C9 Candidats uniques jusqu’à la solution. N.B: il existe des résolutions de taille 2 TDP.
De Robert Mauriès
(Publié le 21/01/2021)
@ François C : Bonjour François. Belle résolution en trois étapes avec des pistes relativement courtes. Sauf erreur de ma part, cela correspond à 3 braids. Avez-vous une résolution avec uniquement des whips ?
De Claude Renault
(Publié le 21/01/2021)
5L5C4 solution P(5L4C4).P(4L4C5) invalide ; P(5L4C4).P(1L6C3) et P(5L4C4).P(6L6C3) invalides
De François C.
(Publié le 22/01/2021)
@ Robert Mauriès : Bonjour Robert, il s'agit bien de whips, voici la résolution complète avec les vrais whips: Candidats uniques: 7L2C9, 2L3C4, 2L1C7, 8L6C7, 2L7C2, 2L5C3, 2L6C5, 7L9C1, 4L8C3 Alignement: 5L1B3 => -5L2C7 -5L2C8 -5L3C8 -5L3C9 Alignement: 5C4B5 => -5L4C6 -5L5C6 Alignement: 5C7B6 => -5L5C8 whip[10]: r1c9{n3 n5}- r1n3{c9 c5}- r9n3{c5 c2}- r9n5{c2 c3}- c3n9{r9 r4}- r5c2{n9 n1}- r5c8{n1 n3}- r8n3{c8 c4}- r6c4{n3 n6}- r6c3{n6 .} => -3L3C9 Paire 14B3p49 => -1L2C8 -4L2C8 -1L3C8 -4L3C8 Candidats uniques: 6L2C8, 4L7C8 whip[9]: r1c5{n3 n9}- b2n3{r1c5 r3c6}- r3n4{c6 c9}- r6c9{n4 n1}- r7c9{n1 n9}- b8n9{r7c4 r8c4}- c1n9{r8 r4}- b4n3{r4c1 r5c2}- r5c8{n3 .} => -3L1C9 Candidats uniques: 5L1C9, 5L8C8, 1L5C8 whip[11]: r6c4{n3 n6}- r7n6{c4 c1}- r4n6{c1 c3}- c3n9{r4 r9}- r9c9{n9 n1}- r7n1{c7 c6}- r9c5{n1 n3}- r1c5{n3 n9}- c1n9{r1 r4}- c6n9{r4 r5}- c6n7{r5 .} => -3L6C9 Candidats uniques jusqu’à la solution. N.B: je n'ai pas obtenu mieux avec les braids et pour la dernière étape c'est beaucoup plus long.
De Paolo
(Publié le 22/01/2021)
@ François C: Bonjour François. Je n'ai trouvé aucune résolution de taille 2 avec les backdoors de taille 1. Je pense que les résolutions que vous indiquez dans votre premier message indiquent des résolutions qui utilisent des backdoors de taille 2. La première piste invalide libère la backdoor de taille 2 tandis que la deuxième piste invalide le confirme. Vous pouvez rapporter au moins une résolution de taille 2. Aussi je voudrais, en référence à votre deuxième message, où vous dites que vous n'avez trouvé meilleures résolutions avec les “ braids “.Je vous rappelle qu'à partir du théorème de Denis Berthier qui indique qu'avec les “braids” il est possible d'obtenir la même résolution que avec T&E, il doit évidemment y avoir deux” braids “qui conduisent à une solution de taille 2 comme vous l'avez indiqué dans votre premier message avec la TDP .
De Robert Mauriès
(Publié le 22/01/2021)
@ Paolo : Bonjour Paolo. François vous répondra certainement. Le théorème de Berthier indique l'équivalence entre les braids et T&E(single,1), donc avec des pistes construites qu'avec des simples. Niveau 2 TDP n'impose pas que l'on utilise des pistes construites qu'avec des simples. Je pense que François a trouvé une taille 2 mais avec des ensembles, ce qui n'est pas résolvable avec des braids, mais peut-être avec des S-braids ou S-whips.
De Paolo
(Publié le 22/01/2021)
@ Robert Mauriès,François C: Bonjour Robert, Nous convenons que ce seront des S-braids. Donc je suppose que la backdoor de taille 1 ou 2 utilisée pour la résolution est une P (E). Je voudrais poser la question suivante: Quand un P (E) est une backdoor, où E est défini par {A1; A2;… .; An} il est vrai que l'une des pistes P (Ax) est une backdoor tandis que toutes les autres P (Ai) conduisent-ils à une contradiction, que E contienne ou non une backdoor?
De Robert Mauriès
(Publié le 22/01/2021)
@ Paolo : Je me suis certainement mal exprimé concernant le taille 2 que François a certainement trouvée. Ce que j'ai voulu dire c'est qu'il a peut-être utilisé un TB-Backdoor et non un single-backdoor, donc une piste TB-valide dont le développement nécessite d'utiliser des alignements et des ensembles fermés (doublet, triplet,..), et pas seulement un ensemble générateur E. Concernant votre question, si P(E) est valide alors forcément c'est que un élément A de E est un backdoor, mais on ne sait pas lequel à priori.
De François C.
(Publié le 22/01/2021)
@ Paolo : Bonsoir Paolo, Il y a quelques résolutions de taille 2 qui utilisent un backdoor de taille 1, mais elles utilisent des ensembles. En voici une : P(3L7C6) => solution P’(3L7C6) . P(3L14C5) => contradiction P’(3L7C6) . P(3L89C5) => contradiction Mais il n’y a pas de résolution de taille 2 qui utilise un backdoor (A,B) de taille 2, c’est-à-dire comme ceci : P(A) . P(B) => solution P(A) . P’(B) => contradiction P’(A) => contradiction En fait il n’y a pas de résolution de taille 2 sans ensembles. Comme les braids n’utilisent pas d’ensembles il n’y a pas de résolution avec seulement 2 braids. Mais ce n’est pas ce que j’ai voulu dire en disant « je n’ai pas obtenu mieux avec les braids ». Ce que j’ai voulu dire c’est que aucun des 3 whips de ma résolution ne peut être remplacé par un braid de taille inférieure.
De Paolo
(Publié le 22/01/2021)
@ Robert Mauriès,François C: Bonsoir Robert et François Très belle résolution de taille 2, je pense unique pour la backdoor P (3L7C6). Je vous pose une question relative aux théorèmes de Denis Berthier sur l'équivalence des résultats obtenus avec les braids et les différentes définitions de T&E données par Denis Berthier voir http://forum.enjoysudoku.com/spiral-8-3-t38475-15.html .Puisque cette résolution ne peut pas être interprétée comme l'application de deux braids (y compris les formes plus complexes avec le terme braids), étant donné l'équivalence des résultats d'une braid avec ceux obtenus avec T&E (également dans ce cas, je veux dire tous les formes plus complexes), voir théorèmes, cette résolution peut-elle aussi être interprétée comme une forme de T&E?
De François C.
(Publié le 23/01/2021)
@ Robert Mauriès : Bonjour à tous, Je crois qu’il y a une ambiguité sur la notion d’ensemble. Personnellement je fais la distinction entre: 1) l’ensemble issu d’une piste. 2) les ensembles que l’on peut utiliser lors de la construction d’une piste. Je dirai qu’une piste est à candidats uniques si elle peut se développer en ne plaçant que des « simples » càd des candidats uniques (qu’elle soit issue d’un candidat ou d’un ensemble). Quand j’ai dit qu’il n’y avait pas de résolution de taille 2 sans ensembles, je parlais d’ensembles de la catégorie 1. C’est-à-dire qu’il n’y a pas de résolution de taille 2 avec seulement des pistes issues d’un candidat. Dans ma résolution de taille 2 plus haut, il y a des pistes issues d’ensembles et qui ne sont pas toutes à candidats uniques. Mais voici une résolution de taille 2 avec des pistes issues d’ensembles et toutes à candidats uniques : TB initiales : Candidats uniques: 7L2C9, 2L3C4, 2L1C7, 8L6C7, 2L7C2, 2L5C3, 2L6C5, 7L9C1, 4L8C3 Alignement: 5L1B3 => -5L2C7 -5L2C8 -5L3C8 -5L3C9 Alignement: 5C4B5 => -5L4C6 -5L5C6 Alignement: 5C7B6 => -5L5C8 P(3L89C5) => contradiction (avec candidats uniques) => -3L8C5 -3L9C5 P(1L6C3) => contradiction (avec candidats uniques) => -1L6C3 => candidats uniques jusqu'à la solution La première piste invalide est à candidats uniques mais elles ne correspond pas à un braid pour autant puisque sa cible n'est pas un simple candidat. Berthier n’a pas envisagé (je crois) la notion de braid ayant pour cible un ensemble. La raison est que si on trouve un braid de cible A1 de taille minimale t1 et un braid de cible A2 de taille minimale t2, alors tout "braid" de cible {A1,A2} serait de taille >= max(t1,t2). Or ce qui l’intéresse ce n’est pas de minimiser le nombre de braids mais leur taille.
De François C.
(Publié le 23/01/2021)
@ Paolo : Voici ma réponse concernant les ensembles backdoors. Pour que ce soit clair, posons d’abord les définitions suivantes : -Un candidat A est un TB-backdoor lorsque P(A) => solution avec les seules TB. -Un ensemble E = {A1…An} est un TB-backdoor lorsque P(E) => solution avec les seules TB. -Un candidat A est un TB-anti-backdoor lorsque P(A) => contradiction avec les seules TB -Un ensemble E = {A1…An} est un TB-anti-backdoor lorsque P(E) => contradiction avec les seules TB. Si E = {A1…An} est inclus dans une entité on peut démontrer facilement que : 1) Si E est un TB-backdoor alors il y a au moins un Ai TB-backdoor et les autres Ai sont tous des TB-anti-backdoor. (évidemment si la grille a une solution unique, il n’y a qu’un seul Ai TB-backdoor). 2) Si E est un TB-anti-backdoor alors tous les Ai de E sont des TB-anti-backdoors. N.B : j’utilise ces 2 propriétés dans mon programme d’optimisation de la taille d’une résolution de façon à ne pas développer inutilement des pistes issues d’ensembles.
De François C.
(Publié le 23/01/2021)
@ Paolo : Vous avez posé la question : « cette résolution peut-elle aussi être interprétée comme une forme de T&E » Bien sûr que le résultat final peut être interprété comme un résultat du T&E, sauf que le résultat donné par l’algorithme rudimentaire du T&E serait beaucoup plus long, fastidieux à vérifier à la main et donc sans grand intérêt. En effet le T&E ne fait aucune optimisation ni dans le nombre d’essais ni dans la longueur des chaînes de contradictions. Donc je n’emploierais pas le terme de T&E pour ma résolution (je parle de la première ou de la dernière car dans l'autre il y a une bifurcation). Mais il est indéniable que l’algorithme dominant de mon programme consiste à faire des essais et qu’il n’y a pas de grande stratégie en dehors de tester toutes les combinaisons possibles.
De François C.
(Publié le 08/03/2021)
Bonjour, En fait il y a au moins une résolution de taille 2 avec des pistes issues de simples candidats, ce qui contredit ce que j’avais dit plus haut. TB initiales puis : P(3L8C4) => contradiction P(69L8C4). P(8L1C1) => contradiction P(69L8C4). P(9L1C1) => solution Bien sûr P(69L8C4) est issue d’un ensemble mais on peut écrire cette résolution de la façon suivante : TB initiales puis : P(3L8C4) => contradiction => - 3L8C4 Aucune TB après cette suppression. P(8L1C1) => contradiction => -8L1C1 TB => solution On voit bien que les 2 pistes utilisées sont issues de simples candidats. :--)
De Didier Griffaut
(Publié le 15/12/2021)
Bonsoir, Après les simplification TB, les pistes 9L1C1 puis 1L9C5 donnent la solution.
Ajouter un commentaire
La solution
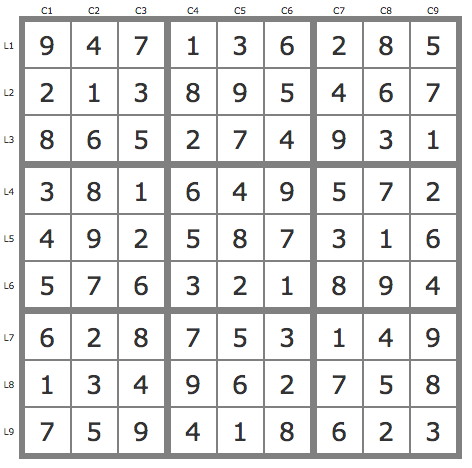
 En savoir plus ...
En savoir plus ...




