S'identifier S'inscrire
assistant-sudoku.com
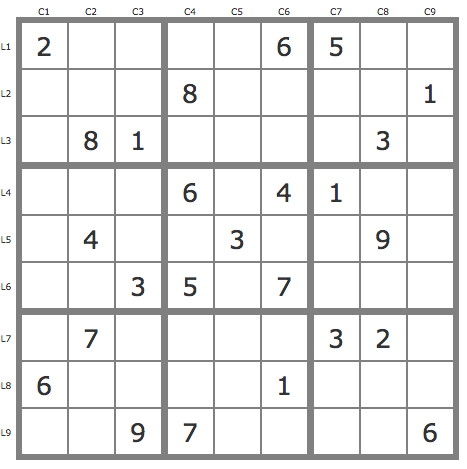
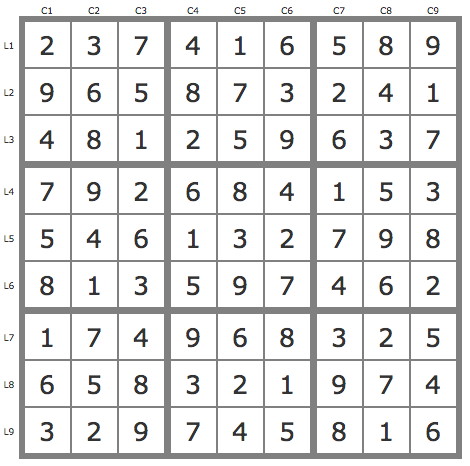
Grille Sudoku résolue
La grille -684Grille de niveau 14/15 conventionnel et de niveau 3 TDP.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 26/10/2020)
Résolution détaillée dans "Voir la résolution".
De Claude Renault
(Publié le 26/10/2020)
11 placements, 1 alignement 3L1C2 solution (backdoor) ; 9L1C2 .(2L2C7-2L3C9) 8 éliminations ; 9L1C2.4-5-7L3C1 invalides
De Paolo
(Publié le 26/10/2020)
Bonjour. 1) 11 placements par les TB initiales. P(25L8C2)=>couvre la grille 2)P(3L8C2).P(4L7C3)=>invalide 3)P(3L8C2).P(8L7C3)=>invalide 4)P(3L8C2).P(5L7C3)=>invalide =>solution ou P(9L2C1)=>couvre la grille 2)P(9L2C6).P(2L3C6)=>invalide 3)P(9L2C6).P(5L3C6)=>invalide 4)P(9L2C7)=>invalide =>solution
De Antoine Gillot
(Publié le 14/01/2025)
Bonjour, alors après les TB, piste 3 l9c1 couvre la grille.
Ajouter un commentaire
La solution
La grille est d'abord simplifiée avec les TB (11 placements).
Voici ensuite comment on peut résoudre avec la TDP en 3 étapes :
P'(5L2C3) est invalide puisqu'elle ne peut pas avoir de candidat 2 dans B2, donc L2C3=5
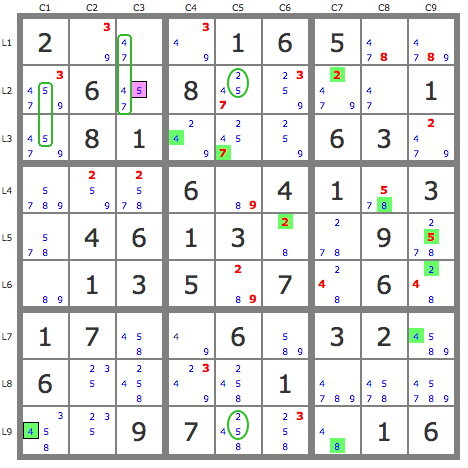 Dès lors,
P(2L4C2) est invalide puisqu'elle ne peut pas avoir de candidat 2 dans B8, on peut donc éliminer 2L4C2, ce qui entraine L4C3=2 et L1C3=7.
Dès lors,
P(2L4C2) est invalide puisqu'elle ne peut pas avoir de candidat 2 dans B8, on peut donc éliminer 2L4C2, ce qui entraine L4C3=2 et L1C3=7.
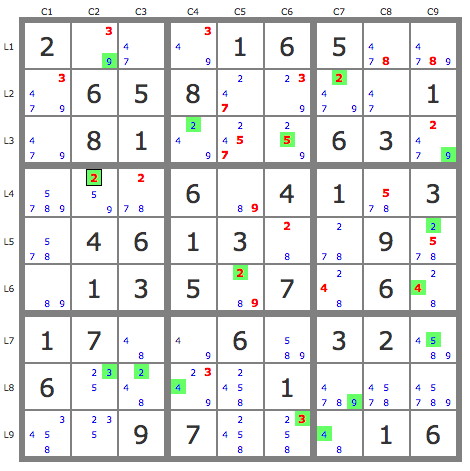 Dès lors,
P(5L4C2) est invalide puisqu'elle ne peut pas avoir de candidat 9 sur C2, on peut donc éliminer 5L4C2, ce qui entraine L4C2=9 et la grille se termine par induction (candidats uniques).
Dès lors,
P(5L4C2) est invalide puisqu'elle ne peut pas avoir de candidat 9 sur C2, on peut donc éliminer 5L4C2, ce qui entraine L4C2=9 et la grille se termine par induction (candidats uniques).
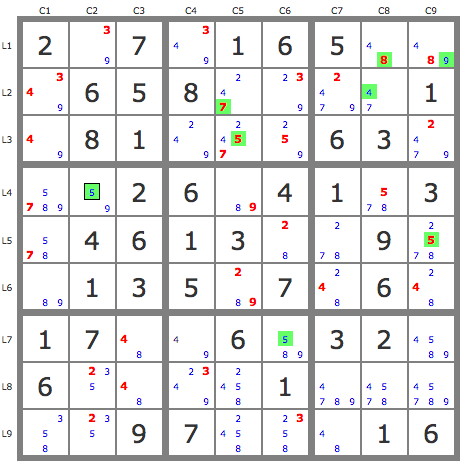
 En savoir plus ...
En savoir plus ...




