S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
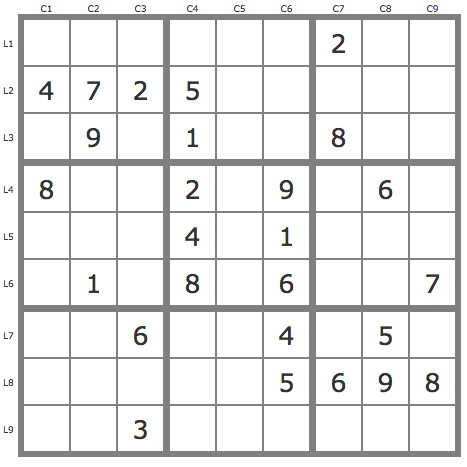
La grille -683Grille de niveau 1 TDP.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 20/10/2020)
12 placements par les TB puis un jeu de pistes issues de la paire 37L1C6. P(7L1C6) couvre la grille, P(3L1C6) est invalide.
De Paolo
(Publié le 20/10/2020)
Bonjour 1) 12 placements par les TB initiales. P(9L2C7)=>couvre la grille 2)P(9L2C9)=> contradiction =>solution La résolution est également possible en croisant les pistes P (9L2C7) et P (9L2C9), en utilisant le développement complet du P (9L2C7) jusqu'à la solution et seulement un développement partiel du P (9L2C9) (sans prouvant que la piste est invalide). De cette manière, insérer les candidats communs aux deux pistes (L1C2 = 6; L3C1 = 3; L5C1 = 6; L7C9 = 3; L9C1 = 9; L9C4 = 6) avec les 12 placements par les TB initiaux, la solution est atteinte.
De Claude Renault
(Publié le 20/10/2020)
trouvé même résolution que Robert
De Robert Mauriès
(Publié le 21/10/2020)
@ Claude Renault : Bonjour Claude. Pour faire autrement, je propose donc dans "Voir la résolution" une résolution pas à pas avec des antipistes courtes.
De Francis Labetoulle
(Publié le 21/10/2020)
Quelles motivations pour choisir les 6 de B3?
De Claude Renault
(Publié le 24/10/2020)
@ Robert Mauriès : bonjour Robert J'ai éprouvé le besoin de de définir de façon simple et claire la notion de visibilité au Sudoku ; je suis arrivé aux definitions suivantes ; vous mé direz si vous êtes d'accord : 1) on dit que 2 candidats se voient, s'ils sont dans la même zone et identiques ou dans la même case et différents ; dans les 2 cas, ils possèdent la même propriété : l'opposition 2) on dit qu'un candidat voit une piste, quand il voit au moins un composant de cette piste Il s'ensuit la propriété suivante : dans un jeu de pistes conjuguées, tout candidat qui voit l'ensemble des pistes peut être éliminé (principe selon lequel un candidat opposé à 2 candidats conjugués peut être éliminé) 1er exemple : jeu de 3 pistes conjuguées P1,P2,P3 : x présent dans une case contenant P1 et P2 et sur une ligne contenant P3 peut être éliminé 2eme exemple : lors de l'utilisation d'une antipiste courte P'(x), on peut, non seulement éliminer les candidats identiques à x qui voient à la fois x et P'(x) mais aussi ceux qui sont dans la même case que x et qui voient P'(x)
De Robert Mauriès
(Publié le 24/10/2020)
@ Claude Renault : Bonjour Claude. Vos définitions 1 et 2 sont exactement les miennes, donc je suis d'accord avec vous. D'accord aussi pour l'exemple 2, mais dans l'exemple 1 je ne sais pas ce que vous entendez par "une case contenant une piste" ?
De Robert Mauriès
(Publié le 24/10/2020)
Bonjour à tous. Voici une résolution avec une seule antipiste composée de seulement 9 candidats : P'(6L2C9) : (-6L2C9)=>6L2C5->8L2C6->7L9C6->[(7L7C7->3L7C9)->9L7C4->2L7C1->2L5C2]->9L5C9 => -9L2C9 => L2C7=9 et fin de la grille par les TB. Il est possible aussi de résoudre avec la seule antipiste P'(7L9C7) limitée à 13 candidats afin d'éliminer le 7L9C6 et ainsi placer le backdoor 8L9C6 (Voir http://forum.enjoysudoku.com/robert-s-puzzles-2020-10-20-t38354.html#p296578)
De Claude Renault
(Publié le 24/10/2020)
@ Robert Mauriès : j'aurais dû dire : une case contenant un composant des 2 pistes
De Robert Mauriès
(Publié le 24/10/2020)
@ Claude Renault : Merci alors de reformuler l'exemple 1.
De Claude Renault
(Publié le 25/10/2020)
@ Robert Mauriès : pour préciser comme vous me le demandez : Premier exemple : jeu de 3 pistes conjuguées P1,P2,P3 : x présent dans une case contenant un composant de P1 et un composant de P2 et sur une ligne contenant un composant de P3 peut être éliminé (ceci pour preciser la configuration qui pourrait s'exprimer simplement par "x voit à la fois P1, P2 et P3)
Ajouter un commentaire
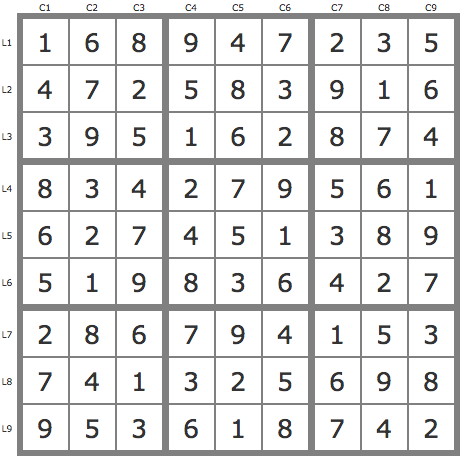
La solution
12 placements par les TB puis un jeu de pistes issues de la paire 37L1C6.
P(7L1C6) couvre la grille, P(3L1C6) est invalide.
Mais voici une résolution pas à pas avec des antipistes limitées à 4 candidats au plus.
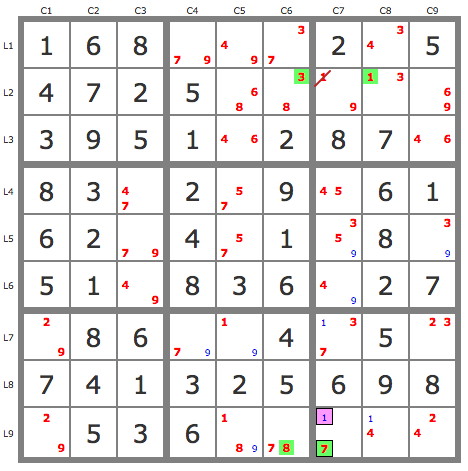
P'(8L9C6) : (-8L9C6)=>7L9C6->(7L7C7->3L7C9)->1L7C5 => -8L7C5 => L7C2=8
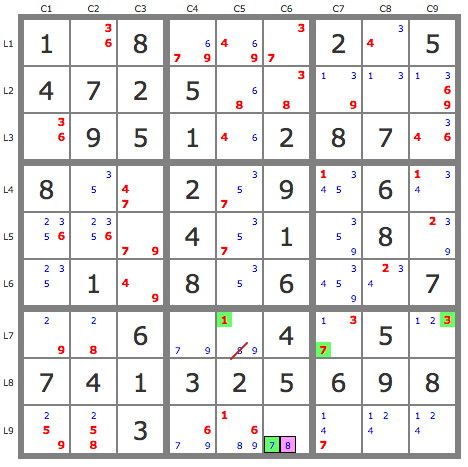 P'(2L7C1) : (-2L7C1)=>2L7C9->2L6C8 => -2L6C1 => 2L6C8 + simplification par TB (6 placements).
P'(2L7C1) : (-2L7C1)=>2L7C9->2L6C8 => -2L6C1 => 2L6C8 + simplification par TB (6 placements).
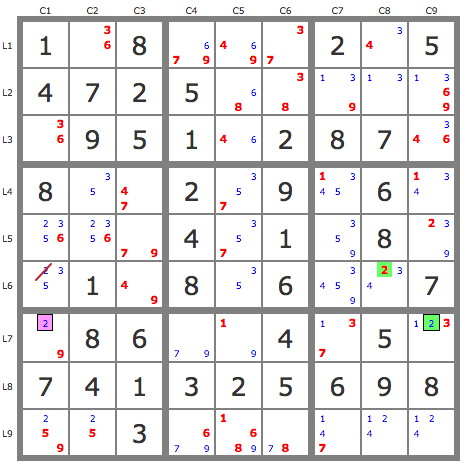 P'(1L2C7) : (-1L2C7)=>9L1C7->4L6C7->1L4C9 => -1L4C7, -1L2C9 => L4C9=1 => -4L9C7.
P'(1L2C7) : (-1L2C7)=>9L1C7->4L6C7->1L4C9 => -1L4C7, -1L2C9 => L4C9=1 => -4L9C7.
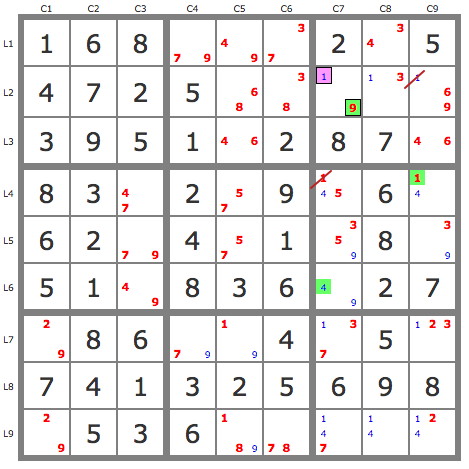 P'(1L9C7) : (-1L9C7)=>7L9C7->8L9C6->3L2C6->1L2C8 => -1L2C7 => L2C7=9 et solution par induction (candidats uniques).
P'(1L9C7) : (-1L9C7)=>7L9C7->8L9C6->3L2C6->1L2C8 => -1L2C7 => L2C7=9 et solution par induction (candidats uniques).
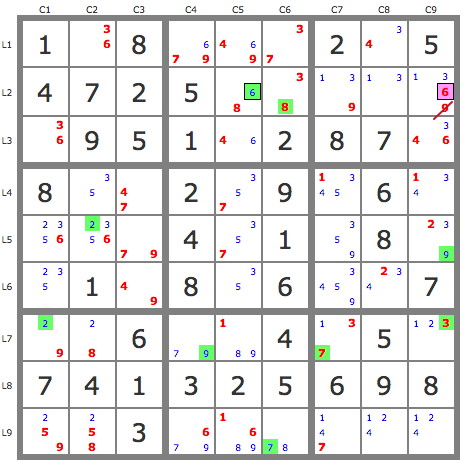
 On peut aussi, résoudre avec une seule antipiste de longueur plus importante (9 candidats) comme ceci :
P'(6L2C9) : (-6L2C9)=>6L2C5->8L2C6->7L9C6->[(7L7C7->3L7C9)->9L7C4->2L7C1->2L5C2]->9L5C9 => -9L2C9 => L2C7=9 et fin de la grille par les TB.
On peut aussi, résoudre avec une seule antipiste de longueur plus importante (9 candidats) comme ceci :
P'(6L2C9) : (-6L2C9)=>6L2C5->8L2C6->7L9C6->[(7L7C7->3L7C9)->9L7C4->2L7C1->2L5C2]->9L5C9 => -9L2C9 => L2C7=9 et fin de la grille par les TB.
 En savoir plus ...
En savoir plus ...




