S'identifier S'inscrire
assistant-sudoku.com
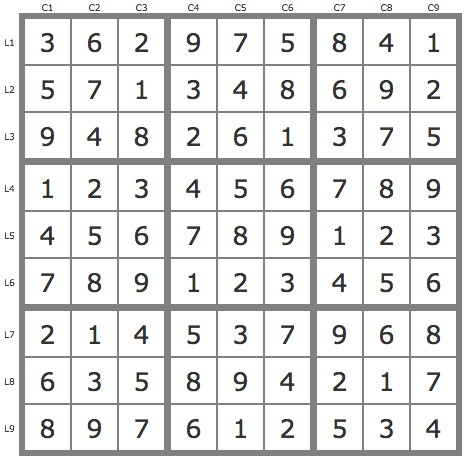
Grille Sudoku résolue
La grille -680Cette grille a été proposée par Denis Berthier sur le forum enjoysudoku.com (http://forum.enjoysudoku.com/myth-buster-t38283.html) pour une particularité commentée par Denis Berthier.
Son niveau TDP est de 1.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 05/10/2020)
Résolution détaillée dans "Voir la résolution".
De Claude Renault
(Publié le 05/10/2020)
P(2L9C6) solution ; P'(2L9C6) invalide
De Robert Mauriès
(Publié le 05/10/2020)
@ Claude Renault : Bonjour Claude. Si 6L9C6 est bien un backoor, en revanche je ne vois pas que P'(6L9C6) est directement invalide. Pouvez-vous vérifier ?
De Paolo
(Publié le 05/10/2020)
Bonsoir 1) 7 placements par les TB initiales. P(1L2C3)=>couvre la grille 2)P’(1L2C3)=> contradiction =>solution. ou 1) 7 placements par les TB initiales. P(2L7C1)=>couvre la grille 2)P’(2L7C1)=> contradiction =>solution. Comme le dit Denis Berthier, cette grille peut être résolue avec T&E (1). Contrairement à d'autres grilles, il ne peut être résolu avec une seule AIC car la démonstration de l'invalidité de P '(1L2C3) ou de P’(2L4C2) est très profonde.
De Francis Labetoulle
(Publié le 06/10/2020)
Bonjour Les choix de départ semblent multiples vu le grand nombre de liens forts en présence après application des TB (dont 7 placements). Essayons, les développements potentiels des deux pistes semblant prometteurs: P1 = P(5L8C3) et P2 (48L8C3). Ces deux pistes, conjuguées par partition de la case L8C3, se croisent et permettent de multiples éliminations, jusqu'à couvrir la grille, la première citée donnant la solution, donc unique. À part celà, la théorie des pistes permet-elle de vérifier l'aspect original mentionné par son créateur ?
De Claude Renault
(Publié le 06/10/2020)
@ Robert Mauriès : vous avez raison Robert ; j'ai dû faire une erreur quelque part
Ajouter un commentaire
La solution
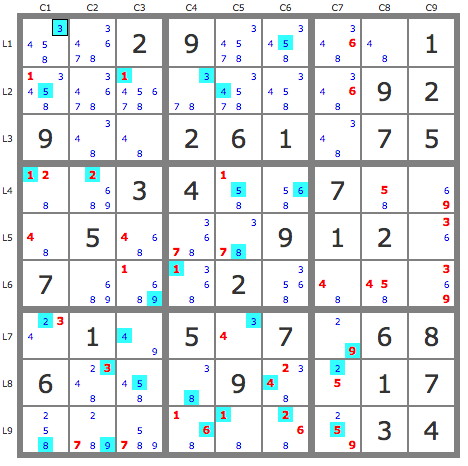
On peut vérifier le niveau de la grille avec la paire 29L7C7 :
P(9L7C7) couvre la grille et P(2L7C7) est invalide.
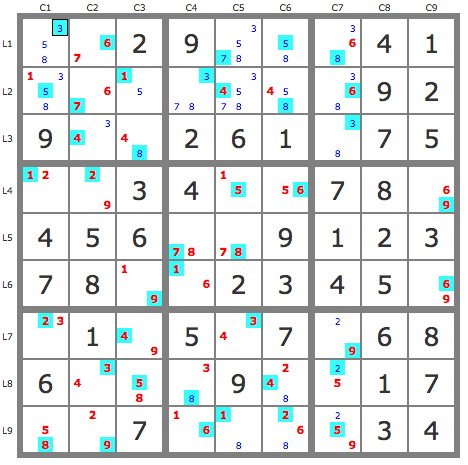
A noter qu'après simplification par les TB, la grille compte 28 backdoors marqués en bleu sur la grille suivante:
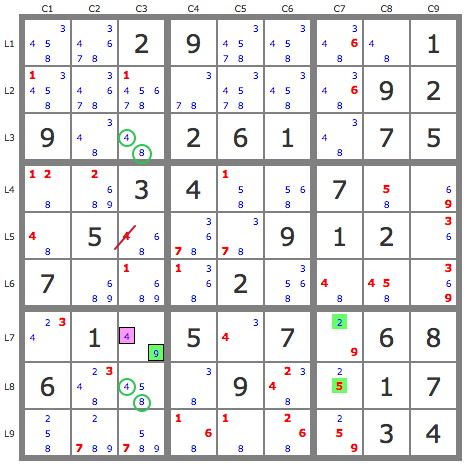
 Une autre approche "pas à pas" est la suivante avec des antipistes successives limitées à 6 candidats au plus (les antipistes sont marquées en vert) :
P'(4L7C3) => -4L5C3 => L5C1=4
Une autre approche "pas à pas" est la suivante avec des antipistes successives limitées à 6 candidats au plus (les antipistes sont marquées en vert) :
P'(4L7C3) => -4L5C3 => L5C1=4
 P(8L3C3) => -8L2569C3 => L5C3=6.
P(8L3C3) => -8L2569C3 => L5C3=6.
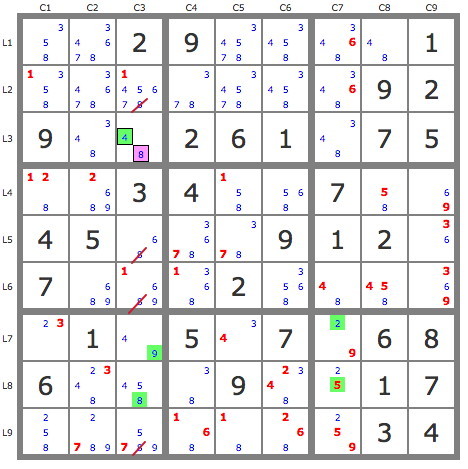 Les TB simplifient alors significativement la grille
Les TB simplifient alors significativement la grille
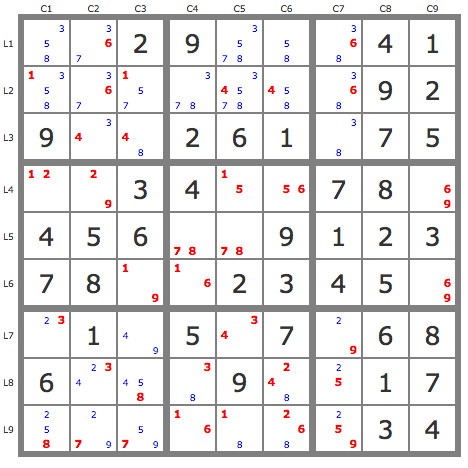 P'(2L4C2) => -2L8C2 et les TB entraînent L9C3=7.
P'(2L4C2) => -2L8C2 et les TB entraînent L9C3=7.
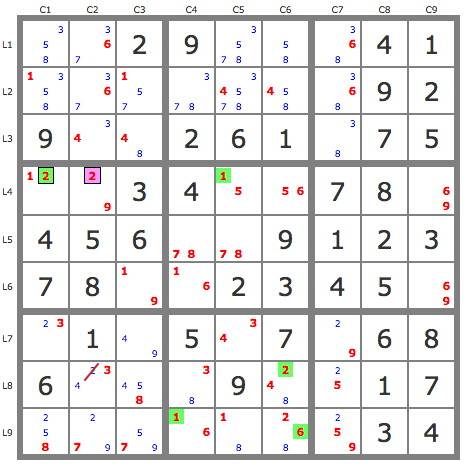 Dès lors, la grille simplifiée compte un backdoor par case qui sont marqués en bleu sur la grille.
Dès lors, la grille simplifiée compte un backdoor par case qui sont marqués en bleu sur la grille.
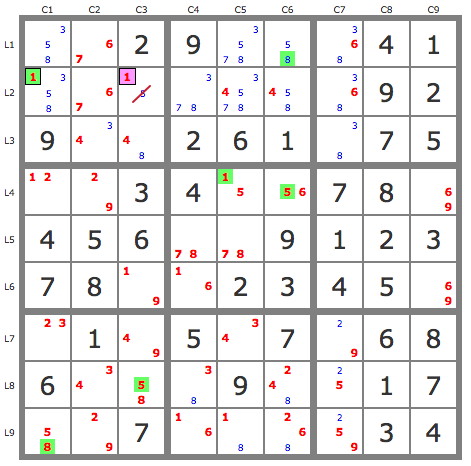
 P'(1L2C3) => -5L2C3 => L2C3=1 et la grille se termine par simple induction (candidats uniques).
P'(1L2C3) => -5L2C3 => L2C3=1 et la grille se termine par simple induction (candidats uniques).
 En savoir plus ...
En savoir plus ...




