S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -674Grille à solution unique plus difficile que son niveau 11 conventionnel ne le laisse paraître.
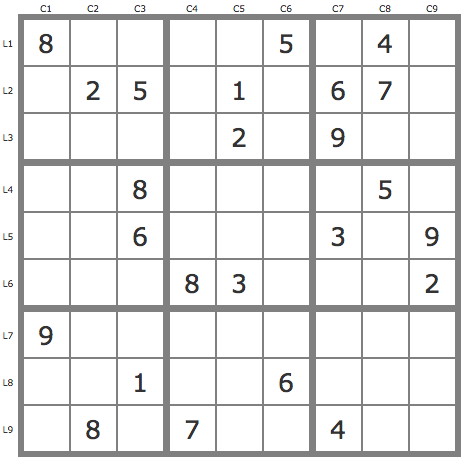
Commentaires sur cette grille
De Claude Renault
(Publié le 03/05/2020)
9 placements par TB P(9L8C5).P(1L3C8) invalide ; P(9L8C5).P(1L7C8).P(4L3C4) solution P(9L8C5).P(1L7C8).P(6L3C4) invalide ; P(9L9C5).P(3L4C1) et P(9L9C5).P(3L4C2) invalides ; niveau tdp 4
De Francis Labetoulle
(Publié le 03/05/2020)
Bonjour P'(1L1C9) -> 0 solution. puis P'(9L9C8) ->0 solution. Puis P'(4L2C1) -> 0 solution , puis solution unique. Cette troisième étape peut être omise si on utilise un *wing des 3 de C4 visuellement immédiat...
De Paolo
(Publié le 03/05/2020)
1) 9 placement par les TB initiales. 2)P(3L2C1)=>contradiction -3L2C1+4L2C1+4L3C4+6L1C4 3)P(5L5C5)=>contradiction =>-5L5C5+4L5C5+4L8C2+5L5C4+4L6C3+9L1C3+4L7C6 P(1L3C1)=>couvre la grille 4)P’(1L3C1)=>contradiction =>solution.
De François C.
(Publié le 04/05/2020)
Bonjour, Les TB initiales => Candidats uniques: 2L1C7,5L3C9,8L5C8,8L3C6,8L2C9,6L6C8,4L4C9,7L1C5,6L4C5 Alignement: 9-L2-B2-L2C4-L2C6 => -9L1C4 Alignement: 5-L6-B4-L6C1-L6C2 => -5L5C1 -5L5C2 Alignement: 2-C3-B7-L7C3-L9C3 => -2L8C1 -2L9C1 Alignement: 9-C5-B8-L8C5-L9C5 => -9L8C4 -9L9C6 Alignement: 7-C9-B9-L7C9-L8C9 => -7L7C7 -7L8C7 Alignement: 1-B6-C7-L4C7-L6C7 => -1L7C7 Ensuite, en 3 étapes : 1) P(9L6C3) = {9L6C3,3L1C3,4L2C1,4L3C4,4L7C3,4L8C5,5L5C5,8L7C5,5L7C7,5L8C4,2L8C8,..} => 9L8 vide => -9L6C3 Candidat unique: 9L1C3 2) P(9L9C5) = {9L9C5,5L9C1,5L6C2,9L4C2,3L4C1,4L2C1,7L8C1,1L6C1,1L4C7,2L4C4,2L8C8,..} => 9L8 vide => -9L9C5 Candidats uniques: 5L9C5,4L5C5,8L7C5,5L7C7,9L8C5,8L8C7,5L5C4,9L9C8 3) P(3L3C3) = {3L3C3,4L2C1,4L3C4,4L8C2,5L6C2,9L6C6,3L2C6,3L1C9,3L9C1,3L4C2,..} => 9L4 vide => -3L3C3 Alignement: 3-C3-B7-L7C3-L9C3 => -3L7C2 -3L8C1 -3L8C2 -3L9C1 Candidats uniques: 6L9C1,6L7C9,7L8C9 Paire nue: 45-L8-L8C1-L8C2 => -4L8C4 Alignement: 4-L8-B7-L8C1-L8C2 => -4L7C2 -4L7C3 Candidats uniques jusqu’à la fin. N.B : autre possibilité avec 20 pistes invalides de 5 candidats maximum.
De Antoine Gillot
(Publié le 21/01/2025)
Bonjour, après TB, 6 l1c5 invalide 3 l1c3 invalide 4 l6c6 invalide 7 l6c3 invalide 3 l3c3 avec bifurcation 67l3c12 invalide 5 l9c5 couvre la grille Je vois dans les solutions qu'il y avait beaucoup plus simple mais je galere toujours même pour résoudre certaines grilles simples.
Ajouter un commentaire
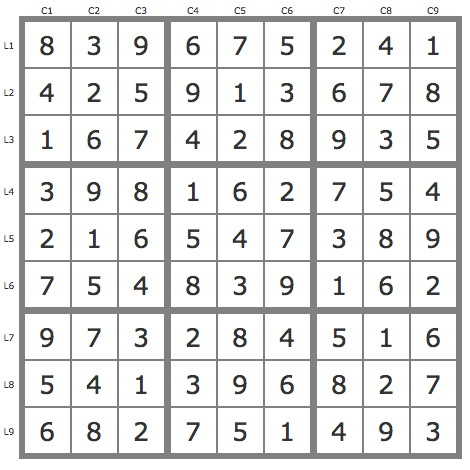
La solution
Réduction de la grille par les TB (9 placements et quelques éliminations), puis :
- JP(34L2C1) => 3 placements, P(3L2C1) étant invalide.
- JP(5B4) => 1 placement, P(5L6C1) étant invalide.
- JP(1L5C2, 47L5C2) => solution, P(4L5C2) et P(7L5C2) étant invalides.
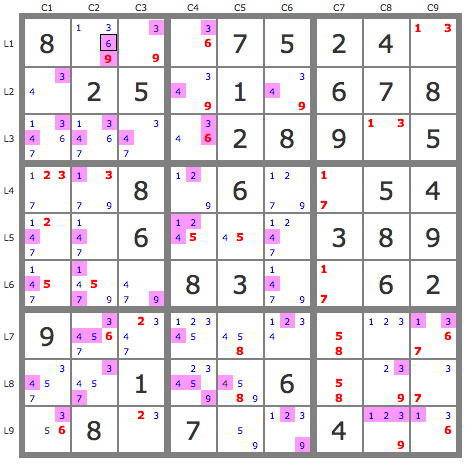
 Analyse de la grille
Nombre de cases à résoudre = 48
Nombre de candidats à résoudre = 160
Nbr de backdoor = 0
Nbr de candidats incertains (piste sans issue) = 111
Nbr de candidats invalides = 49
Les générateurs invalides sont marqués en violet.
Analyse de la grille
Nombre de cases à résoudre = 48
Nombre de candidats à résoudre = 160
Nbr de backdoor = 0
Nbr de candidats incertains (piste sans issue) = 111
Nbr de candidats invalides = 49
Les générateurs invalides sont marqués en violet.
 En savoir plus ...
En savoir plus ...




