S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -673Grille de niveau 11 conventionnel.
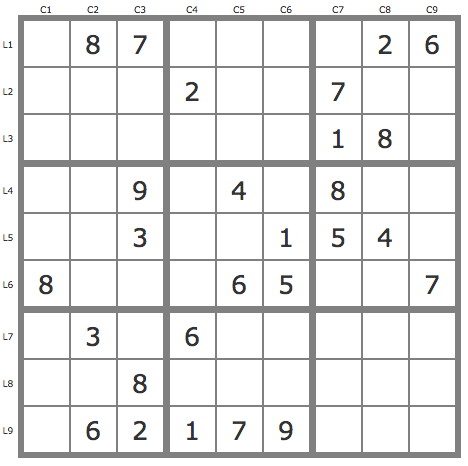
Commentaires sur cette grille
De Robert Mauriès
(Publié le 26/04/2020)
Solution et analyse de la grille accessibles par le lien ci-dessus "Voir la résolution".
De Francis Labetoulle
(Publié le 27/04/2020)
Bonjour P(2L5C9) couvre la grille. P(2L5C5).P(2L6C7) et P(2L5C5).P(3L6C7) sont invalides. D'approche plus"méthodologique": : P(3L6C7) est invalide puis les pistes issues des 2 de B6 se croisent pour couvrir la grille. Je viens de constater que cela est quasi identique au cheminement de Robert...
De Claude Renault
(Publié le 27/04/2020)
P(9L5C5) solution ; P(2L5C5).P(1L6C8) et P(2L5C5).P(9L6C8) invalides
De Paolo
(Publié le 27/04/2020)
Bonjour 1) 6 placement par les TB initiales. 2)P(1L4C9)=>contradiction -1L4C9+1L6C8+4L6C3+2L6C2+2L3C1+2L7C7 P(4L1C6)=>couvre la grille 3)P(3L1C6)=>contradiction =>solution.
De François C.
(Publié le 27/04/2020)
Bonjour, TB initiales: Candidats uniques: 6L5C1, 6L4C8, 6L8C7, 8L9C9, 8L5C4, 7L5C2 Alignement: 3-L9-B9-L9C7-L9C8 => -3L8C8 -3L8C9 Ensuite, avec des pistes invalides courtes : 1) P(3L8C4) = {3L8C4,3L4C6,4L1C6,..} => 4C4 vide => -3L8C4 2) P(2L7C5) = {2L7C5,2L5C9,..} => 2L8 vide => -2L7C5 3) P(9L6C8) = {9L6C8,2L5C9,3L6C7,..} => L6C4 vide => -9L6C8 4) P(4L7C7) = {4L7C7,2L6C7,9L6C4,3L6C8,5L9C8,9L2C8,..} => 9C7 vide => -4L7C7 5) P(3L1C4) = {3L1C4,4L1C6,4L8C4,5L3C4,5L1C1,4L9C1,..} => 4C7 vide => -3L1C4 6) P(4L8C9) = {4L8C9,4L1C7,4L3C4,3L1C6,2L8C6,7L4C6,..} => 7L3 vide => -4L8C9 7) P(2L7C9) = {2L7C9,2L6C7,9L6C4,3L6C8,3L9C7,..} => 4B9 vide => -2L7C9 8) P(4L3C4) = {4L3C4,3L1C6,3L8C5,2L5C5,7L4C6,..} => 7L3 vide => -4L3C4 9) P(5L7C3) = {5L7C3,4L9C1,4L1C7,4L8C4,5L8C5,3L8C6,..} => L1C6 vide => -5L7C3 Alignement: 5-C3-B1-L2C3-L3C3 => -5L1C1 -5L2C1 -5L2C2 -5L3C1 -5L3C2 Alignement: 5-L1-B2-L1C4-L1C5 => -5L2C5 -5L3C4 -5L3C5 Paire nue: 14-C3-L6C3-L7C3 => -1L2C3 -4L2C3 -4L3C3 Paire cachée: 45-C4-L1C4-L8C4 => -9L1C4 10) P(4L7C3) = {4L7C3,1L6C3,3L6C8,5L9C8,..} => L9C1 vide => -4L7C3 Candidat unique: 1L7C3 Candidat unique: 4L6C3 11) P(5L8C2) = {5L8C2,4L9C1,4L1C7,3L1C6,9L3C5,9L1C1,..} => 9C2 vide => -5L8C2 Candidat unique: 5L4C2 12) P(5L8C4) = {5L8C4,5L1C5,1L1C1,9L1C7,2L7C7,2L6C2,..} => L4C1 vide => -5L8C4 Candidat unique: 4L8C4 Candidat unique: 5L1C4 Candidat unique: 9L8C2 Alignement: 4-C2-B1-L2C2-L3C2 => -4L1C1 -4L2C1 -4L3C1 13) P(4L1C7) = {4L1C7,3L1C6,9L3C5,9L6C4,9L7C7,2L7C6,..} => L8C6 vide => -4L1C7 Candidats uniques jusqu’à la fin.
De Robert Mauriès
(Publié le 28/04/2020)
Bonjour à tous. A titre indicatif, j'ai repris, dans le même ordre et en termes d'éliminations successives, le même cheminement que celui de François , mais en utilisant des anti-pistes. Dans l'approche de François, on recherche les candidats générant des pistes invalides. Dans la mienne on recherche les paires (de candidats ou d'ensembles) qui élimineront ces candidats. Evidemment, lorsque le candidat à éliminer fait partie d'une paire, les deux approches sont identiques, c'est le cas des éliminations 12 et 13. Comme François, je me suis donc limité à des anti-pistes de 6 candidats maximum, mais il est assez visible qu'en augmentant ne serait-ce que d'un candidat le nombre de candidats on diminue le nombre d'opérations sensiblement. Il est à noter aussi que François n'utilise que des candidats uniques dans la construction des pistes, alors que moi, pour avoir le même résultat je dois parfois utiliser des ensembles. Enfin, ces cheminements ne sont pas les seuls possibles. D'autres donneront avec plus ou moins de candidats des résolutions différentes, évidemment. Pour alléger les écritures, je note (-A) l'antipiste P'(A). 1) (-3L46C4) => 3L4C6->4L1C6->4L8C4 => -3L8C4 2) (-2L5C5) => 2L5C9->2L7C7 => -2L7C5 3) (-9L6C4) => [(3L6C4 et 9L5C5)->2L5C9]->9L6C7 => -9L6C8 4) (-2L7C7) => (2L6C7->9L6C4->3L6C8->5L9C8->9L2C8)->9L7C7 => -4L7C7 5) (-3L1C6) => 4L1C6->[(4L8C4 et 4L9C7)->5L9C1->5L1C45]->5L1C4 => -3L1C4 6) (-4L8C46) => (4L7C6->8L2C6->6L3C6->7L3C4)->4L1C4->4L9C7 => -4L8C9 7) (-2L7C7) => 2L6C7->9L6C4->3L6C8->3L9C8->4L7C9 => -2L7C9 8) (-4L1C6) => (3L1C6->3L8C5->2L78C6)->7L4C6->7L3C4 => -4L3C4 9) (-5L9C1) => 4L9C1->4L1C7->[(4L8C4 et 3L1C6)->3L8C5]->5L7C5 => -5L7C3 Mêmes éliminations par les TB. 10) (-4L9C1) => 5L9C1->3L9C8->1L6C8->4L6C3 => -4L7C3 Mêmes placements. 11) (-5L9C1) => (4L9C1->4L1C7->3L1C6->9L3C5->9L1C1)->57L78C1 => -5L8C2 Même placement 12 et 13) identiques au cheminement de François mais avec les anti-pistes de ses pistes, car il s'agit d'éliminer des candidats appartenant à des paires. Fin avec les TB.
Ajouter un commentaire
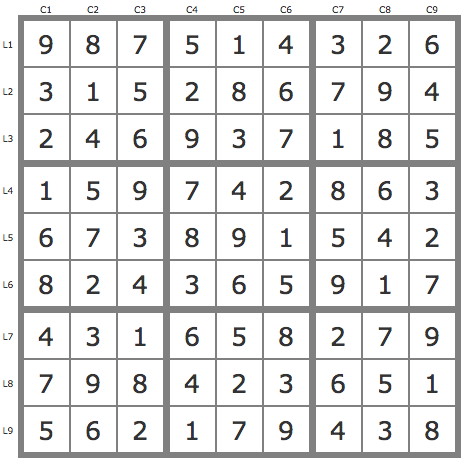
La solution
Après réduction de la grille par les TB, l'analyse de la grille montre qu'une résolution rapide est obtenue avec les candidats de la case L6C7. P(9L6C7) couvre la grille, tandis que P(2L6C7) et P(3L6C7) sont invalides.
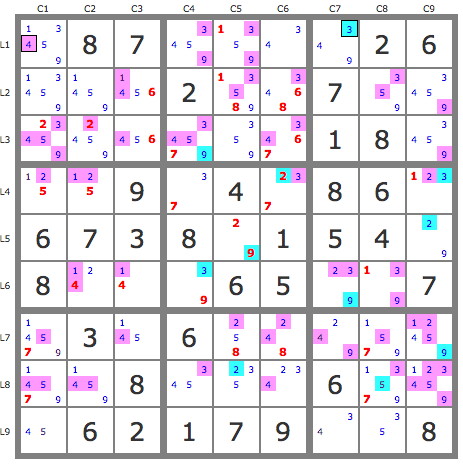
 Analyse de la grille
Nombre de cases à résoudre = 48
Nombre de candidats à résoudre = 167
Nbr de backdoor = 11
Nbr de candidats incertains (piste sans issue) = 96
Nbr de candidats invalides = 60
Les backdoors sont marqués en bleu, les générateurs invalides en violet et les générateurs incertains sont les candidats non marqué d'une couleur.
Analyse de la grille
Nombre de cases à résoudre = 48
Nombre de candidats à résoudre = 167
Nbr de backdoor = 11
Nbr de candidats incertains (piste sans issue) = 96
Nbr de candidats invalides = 60
Les backdoors sont marqués en bleu, les générateurs invalides en violet et les générateurs incertains sont les candidats non marqué d'une couleur.
 En savoir plus ...
En savoir plus ...




