S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -665Grille à solution unique de niveau 10/11 conventionnel.
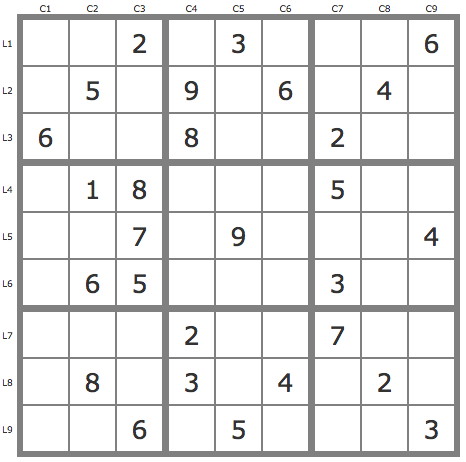
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 19/03/2020)
Bonjour P(5L8C1) couvre la grille. P(5L7C1) s'avère invalide avec la contribution des 9 de L1.( *xwing ou couleurs basiques ou "skyscraper " ou...). À la lecture de la résolution de Claude Renault je constate, et ce n'est pas surprenant, que les 7 de L8 donnent un résultat similaire à celui que j'ai obtenu: P(7L8C5) couvre la grille alors que P(7L8C1) est invalide moyennant le*xwing des 9 de L1...
De Claude Renault
(Publié le 19/03/2020)
6 placements par procédures de base : P(19L8C7) invalide ; P(6L8C7) valide P(1L8C5) invalide ; P(7L8C5) solution
De Robert Mauriès
(Publié le 20/03/2020)
@ Francis Labetoulle : Bonjour Francis. Votre résolution, que ce soit avec les 5C1 ou les 7L8 (comme Claude), est très intéressante car elle permet de résoudre par simple croisement des deux pistes, donc sans constater l'invalidité de l'une ou l'autre des pistes, ceci en raison du skyscraper sur les 9, ou son équivalent une bifurcation sur les 9, permettant par croisement des deux branches puis des deux pistes de placer des candidats et de terminer la grille par les TB. Bravo pour le skyscraper caché !
De François C.
(Publié le 21/03/2020)
Bonjour, En utilisant comme seules TB les candidats uniques (dans case ou zone), même pour les pistes: 3 placements initiaux. Ensuite en considérant la paire 9C7 : P(9L8C7) => contradiction => -9L8C7 => L1C7 = 9 Puis en considérant la paire 7L8 : P(7L8C1) => contradiction => -7L8C1 Enfin 49 placements conduisent à la solution.
De Robert Mauriès
(Publié le 21/03/2020)
Résolution pas-à-pas détaillée dans "Voir la résolution".
Ajouter un commentaire
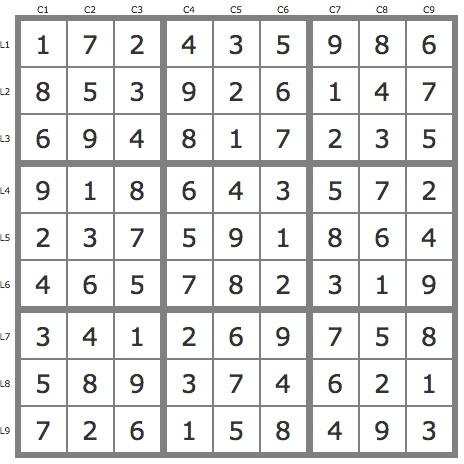
La solution
Après simplification par les TB (6 placements) on utilise la technique des pistes.
1) Utilisation de deux pistes conjugées. (voir schéma)
P(7L8C5) : 7L8C5-> ... ->2L9C2
P(7L8C1) : 7L8C1->(5L8C4->5L1C8)->(bifurcation sur les 9)->(-9)r9c2->2r9c2
=> r2c9=2 => 2 placements et plusieurs éliminations avec les TB.
 2) Utilisation de trois anti-pistes successives.
P'(5L5C4) : -5L5C4->5L5C6->5L3C9->5L8C1->7L8C5->4L4C5->4L1C4 => -5L1C4 => 2 placements and 2 éliminations
P'(9L8C3) : -9L8C3->1L8C3->7L9C1->7L8C5->6L8C7 => -9L8C7 => L1C8=9
P'(7L9C1) : -7L9C1->7L9C4->16L8C57->9L8C3->9L3C2->7L1C2->5L1C6->5L3C9->5L8C1 => -7L8C1, fin avec les TB.
2) Utilisation de trois anti-pistes successives.
P'(5L5C4) : -5L5C4->5L5C6->5L3C9->5L8C1->7L8C5->4L4C5->4L1C4 => -5L1C4 => 2 placements and 2 éliminations
P'(9L8C3) : -9L8C3->1L8C3->7L9C1->7L8C5->6L8C7 => -9L8C7 => L1C8=9
P'(7L9C1) : -7L9C1->7L9C4->16L8C57->9L8C3->9L3C2->7L1C2->5L1C6->5L3C9->5L8C1 => -7L8C1, fin avec les TB.
 En savoir plus ...
En savoir plus ...




