S'identifier S'inscrire
assistant-sudoku.com
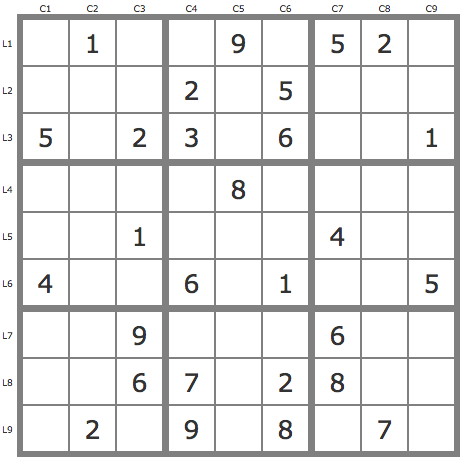
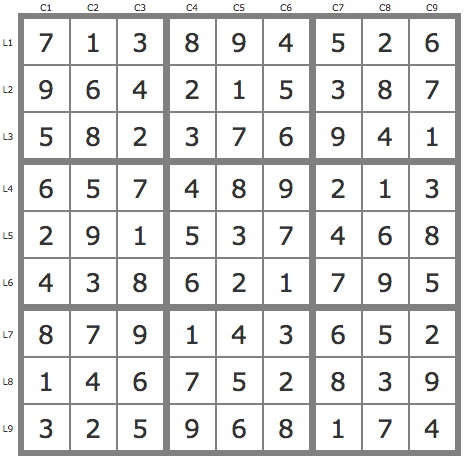
Grille Sudoku résolue
La grille -662Grille de niveau 12 conventionnel.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 06/03/2020)
Indication : paires de B2. Niveau TDP=1
De Francis Labetoulle
(Publié le 06/03/2020)
Bonjour D'un. point de vue méthodologique (cf compléments JC...) les paires de B2 sont d'excellentes candidates et permettent de couvrir la grille. On peut partir pour des raisons similaires de la case L7C6, mais encore de la boucle des 4, qui est ici bien sûr équivalente...
De Claude Renault
(Publié le 07/03/2020)
11 placements par procédures de base P(4L3C5) invalide ; P(7L3C5) solution
De François C.
(Publié le 08/03/2020)
Bonjour, La paire 4B2 fait partie d’un grand réseau de paires équivalentes : 4B2 <=> 4B1 <=> 4B3 <=> 4B8 <=> 47L1C6 <=> 47L3C5 <=> 34L7C6 <=> 4L7C56 etc Chacune de ces paires donne une résolution de taille 1. La seule autre résolution de taille 1 que j’ai trouvée, et qui ne part pas de l’une de ces paires, est basée sur la paire d’ensembles (3L56C5, 3L78C5). En effet P(3L56C5) = P’(3L78C5) = {5L8C5, 4L7C5….} passe donc par un candidat de la paire 4L7C56 (équivalente à 4B2). et P(3L78C5) passe par le 4L7C6 car le 3L7C6 voit l’ensemble 3L78C5. Donc cette piste passe par un candidat de la paire 34L7C6 (équivalente à 4B2).
De Robert Mauriès
(Publié le 09/03/2020)
La résolution de cette grille peut être faites "pas à pas" en ne travaillant qu'avec des anti-pistes de longueurs limitées (nombre d'enchaînements). Un peu comme le fait Denis Berthier avec les biv-chains, les whips et les braids (Voir son livre "Pattern-Based Constraint Satisfaction and Logic Puzzles" disponible sur internet). Dans cet esprit, vous pouvez voir par le lien ci-dessus (Voir la résolution) une résolution en huit étapes successives avec des anti-pistes dont la longueur ne dépasse par 8 enchaînements. Denis Berthier qui a gentillement accepté de résoudre cette grille avec son solveur, obtient des longueurs de whips ne dépassant pas 6 (voir http://forum.enjoysudoku.com/post288303.html#p288303).
De Claude Renault
(Publié le 10/03/2020)
@ Robert Mauriès : je ne comprends pas pourquoi vous utilisez la notion particuliere d'antipiste car, pour moi, une antipiste n'est rien de moins qu'une piste issue d'un ensemble (l'ensemble complémentaire)
De Robert Mauriès
(Publié le 10/03/2020)
@ Claude Renault : Bonjour Claude. Il n'est pas exacte de dire qu'une antipiste P'(E) est la piste P(E') où E' est le complémentaire de E. Cela n'est vrai que si E' est le complémentaire de E dans une même entité, mais cela est faux pour le complémentaire d'un ensemble E dont les candidats ne sont pas contenus dans la même entité. Nous avons déjà eu ce débat il y a quelques années en arrière. Ainsi d'une manière générale les antipistes offrent plus de possibilités que les pistes. Certes, en pratique où ce sont essentiellement des paires qui sont exploitées, pistes et antipistes font le même travail. Toutefois, s'agissant de travailler avec un seul "enchaînement" de candidats, les antipistes ont un avantage sur les pistes car elles disposent d'un théorème qui dit que "tout candidat qui voit à la fois le générateur de l'antipiste et l'antipiste peut être éliminé" et ce que le générateur E soit ou pas dans une entité. Il s'agit donc d'une autre façon d'éliminer des candidats qu'un jeu de pistes conjuguées éliminerait d'une autre façon.
De Claude Renault
(Publié le 10/03/2020)
@ Robert Mauriès : en fait, quand je parle de piste issue d'un ensemble, c'est au sens général, l'ensemble pouvant être simple ou complexe (une ou plusieurs entités) ; quant à la propriété que vous indiquez, ce n'est qu'un cas particulier des cases interactives dans lesquelles il est possible d'éliminer des candidats non seulement à l'origine des pistes conjuguées mais sur l'ensemble des composants de chaque piste
De Claude Renault
(Publié le 10/03/2020)
@ Robert Mauriès : après reflexion, ma dernière conclusion est fausse car les ensembles générés par un jeu de pistes sont coordonnés et non opposés comme le sont les ensembles complémentaires ; la proposition n'est donc valable qu'à l'origine
De Paolo
(Publié le 10/03/2020)
Bonsoir Je rapporte dans http://www.sitohd.com/siti/23142/foto/415468.jpg la représentation des 92 pistes P (A), dans laquelle A est l'un des 92 candidats possibles après l'application de la TB. Les candidats gris sont des backdoors, les candidats avec un arrière-plan non coloré sont les générateurs de piste dont l'invalidité ne peut pas être déterminée tandis que les candidats avec un arrière-plan coloré génèrent des pistes invalides. On peut noter qu'il y a 19 backdoors, dont 13 sont certainement avec anti-piste invalide, il y a aussi 50 candidats qui déterminent des pistes invalides. Dans le diagramme suivant, en plus des backdoors et des pistes invalides, le nombre de candidats éliminés générées par le P (A) pour résoudre la grille ou le nombre de candidats éliminés liées à la piste en question pour démontrer une invalidité ou le nombre de candidats éliminés avant générer un bloc. http://www.sitohd.com/siti/23142/foto/415469.jpg Notez que les pistes invalides qui résolvent la grille avec moins de candidats éliminés sont P(9L7C7) et P(4L7C4).
De Francis Labetoulle
(Publié le 11/03/2020)
@ Robert Mauriès : Merci pour cette information concernant les whips et braids de Denis Berthier. J'avoue avoir quelques réticences à m'investir dans cette étude car, une fois assimilé le principe de ces méthodes, est-il aisé de détecter ces whips et braids sans logiciel ? Si la réponse est négative pour une grille telle que celle-ci, de niveauTDP 1 et de résolution quasi immédiate "à la main", mon enthousiasme naturel est un peu entamé... Un exemple du dernier livre de Denis Berthier, page 233 (fig.8.8.) offre une résolution (mode JC) de niveau1, ce qui n'incite pas le sudokistes pressé à s'investir dans la résolution par "braids" proposée. Mais un puriste ne doit pas hésiter à s'y plonger!
De François C.
(Publié le 11/03/2020)
@ Francis Labetoulle : Bonjour, A mon avis les « whip » et les « braid » inventés par Denis Berthier correspondent en gros à des pistes invalides de la TDP. Donc, pour résumer, le jeu consiste pour lui à trouver les pistes invalides les plus courtes possibles (principe du « simplest first »), ce qui est un casse-tête bien plus compliqué que celui de résoudre la grille. Cette optimisation n’est évidemment faisable que par programme, et elle permet de déterminer un niveau de difficulté de la grille (qui, pour lui, est la longueur de la plus grande piste invalide utilisée).
De François C.
(Publié le 11/03/2020)
… Ceci dit, on peut toujours faire une optimisation relative manuellement (ce qu’a fait Robert pour cette grille) et conclure que le niveau « Berthier » de la grille est inférieur ou égal à la longueur de la plus grande piste invalide utilisée, ici 8 (et 6 avec le logiciel de Berthier). C'est d’ailleurs le même principe pour le niveau TDP: il faut souvent se contenter de le majorer.
De Robert Mauriès
(Publié le 11/03/2020)
@ Francis Labetoulle et François C :
Si en gros François à raison, je pense que Berthier ne serait pas d'accord avec ce raccourci qui réduirait ses techniques à des T&E !
Pour ceux qui résolvent à la main, le concept des whips et des braids est tout de même intéressant car il permet de "déceler plus logiquement" les candidats à éliminer en construisant des chaînes s'appuyant sur des paires. Si alors on ne s'impose pas des longueurs minimales comme le fait Berthier, whips et braids deviennent des outils aussi efficaces que les pistes.
Selon moi, ce sont les antipistes qui se rapprochent le plus de ce que font les whips et les braids.
A titre d'exemple (grille berthier p.231), voici une élimination faite avec les trois méthodes (whip, antipiste, piste)
1) g-whip[4] = B9n9{L789C9 L7C78}-B7n9{L7C123 L89C1}-B4n9{L56C1 L4C23}-B6n9{L4C78.} => -9L123C9 (g-whip car on utilise des groupes)
2) P'(9L789C9) : -9L789C9->9L7C78->9L89C1->9L4C23->9L456C9 => -9L123C9
3) P(9L123C9) : 9L123C9->9L7C78->9L4C23->9L4C23 invalide => -9L123C9
Pour 1) et 2) le raisonnement est d'exploiter la paire d'ensembles 9L789C9/9L7C78, c'est en cela que l'élimination est "décelée plus logiquement", car trouvée comme une conséquence.
De Francis Labetoulle
(Publié le 11/03/2020)
@ Robert Mauriès et François Merci à tous deux d'avoir donné vos points de vue sur cette question délicate. Il me reste à poursuivre la lecture du livre de Denis Berthier... Une petite remarque sur l'exemple cité par Robert : en diagramme CN on voit aisément le 4-uplet (1247) sur la ligne N9. La grille se résout dès lors sans aucune difficulté. Mais là n'est pas la question!
De Robert Mauriès
(Publié le 11/03/2020)
@ Francis Labetoulle : Oui Francis, ce 4-uplet de CN est un Jellyfish sur les 9 dans CL. Un coup d'œil sur ces espaces CN et LN permet, comme c'est le cas ici, de voir des configurations plus difficiles à repérer dans l'espace CL. Il est possible aussi d'utiliser utilement la techniques des pistes dans les espaces CN et LN avec les mêmes propriétés d'élimination et de validation. L'application de l'Assistant Sudoku permet de le faire, et de voir comment se comporte dans chaque espace une piste tracée dans un des espaces.
Ajouter un commentaire
La solution
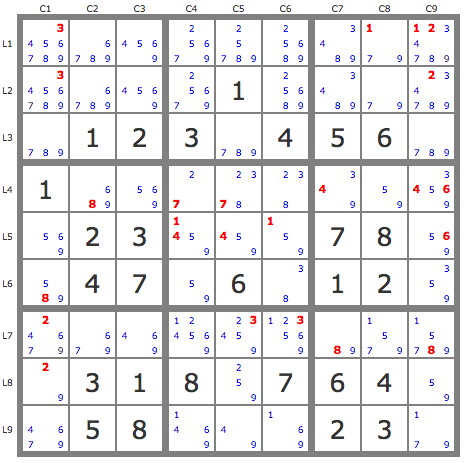
Après réduction de la grille par les TB (11 placements) on utilise des anti-pistes par étapes successives.
1) P'(8L1C3) : -8L6C3->8L1C3->8L5C9 => -8L6C8 , -8L5C12
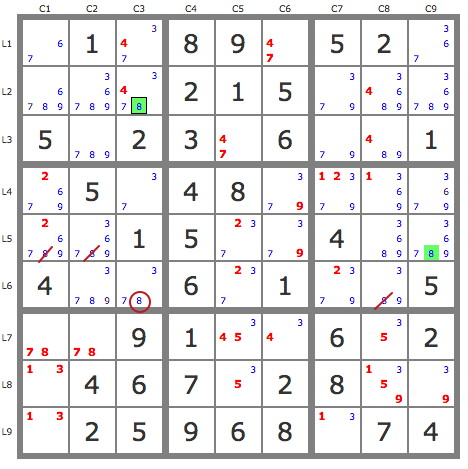 2) P'(9L3C7) : -9L3C7->[7L3C7->7L1C6->4L1C3->3L1C9]->9L2C7 => -9b3C89, -9L46C7
2) P'(9L3C7) : -9L3C7->[7L3C7->7L1C6->4L1C3->3L1C9]->9L2C7 => -9b3C89, -9L46C7
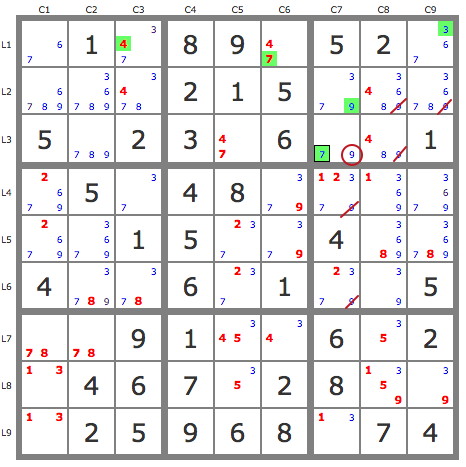 3) P'(8L5C9) : -8L5C9->8L2C9->[(8L3C2 & 4L3C8->7L3C5)->(7L7C2 & 8L6C3)]->7L6C7 => -7L5C9
3) P'(8L5C9) : -8L5C9->8L2C9->[(8L3C2 & 4L3C8->7L3C5)->(7L7C2 & 8L6C3)]->7L6C7 => -7L5C9
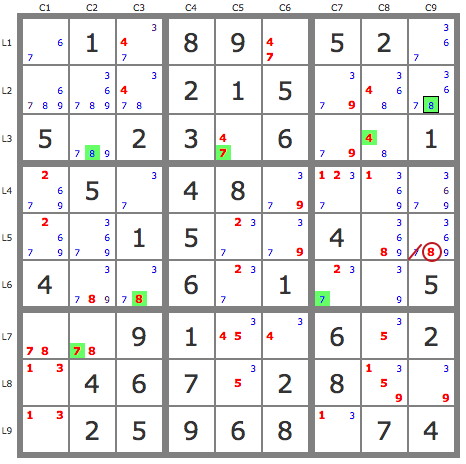 4) P'(7L4C3) : -7L4C3->3L4C3->3L1C9->79L23C7->7L4C9 => -7L4C167
4) P'(7L4C3) : -7L4C3->3L4C3->3L1C9->79L23C7->7L4C9 => -7L4C167
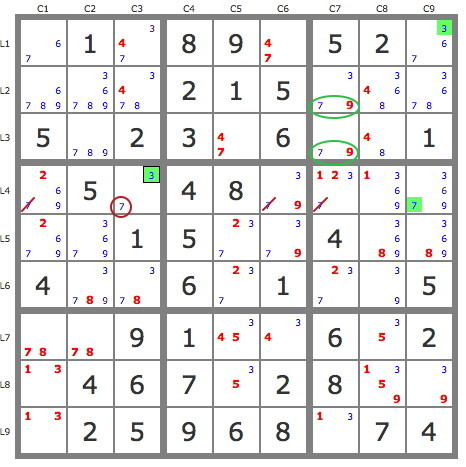 5) P'(7L4C3) : -7L4C3->3L4C3->3L1C9->6L1C1->6L5C2 => -7L5C2
5) P'(7L4C3) : -7L4C3->3L4C3->3L1C9->6L1C1->6L5C2 => -7L5C2
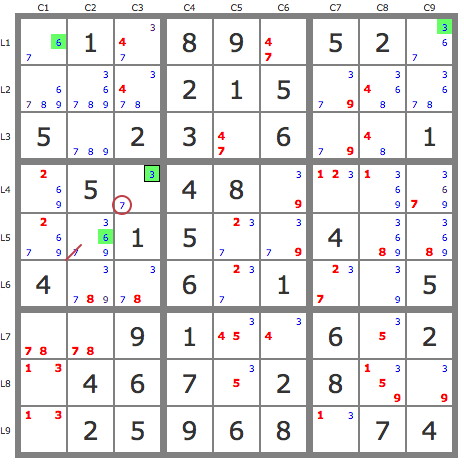 6) P'(7L6C237) : -7L6C237->7L4C9--> ... ->7L3C5 => -7L6C5 => -7L5C1 (voir le schéma)
[-7L6C237->7L4C9->3L4C3->9L4C6]->7L5C2->7L7C2------->7L3C5
| | |
---------->9L56C2->9L3C7
6) P'(7L6C237) : -7L6C237->7L4C9--> ... ->7L3C5 => -7L6C5 => -7L5C1 (voir le schéma)
[-7L6C237->7L4C9->3L4C3->9L4C6]->7L5C2->7L7C2------->7L3C5
| | |
---------->9L56C2->9L3C7
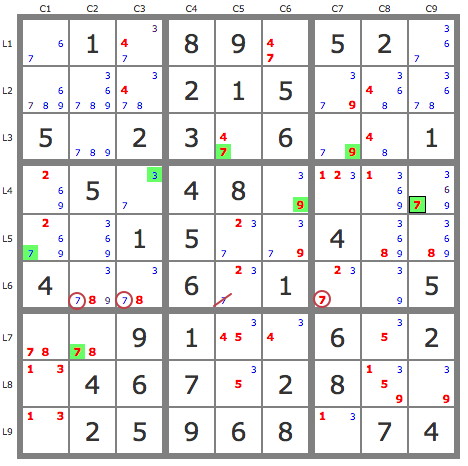 P'(9L4C6) : -9L4C6->3L4C6->7L4C3->(7L6C7->9L3C7)->3L2C7->3L1C3->4L1C6->7L5C6 => -9L5C6 => L4C6=9
P'(9L4C6) : -9L4C6->3L4C6->7L4C3->(7L6C7->9L3C7)->3L2C7->3L1C3->4L1C6->7L5C6 => -9L5C6 => L4C6=9
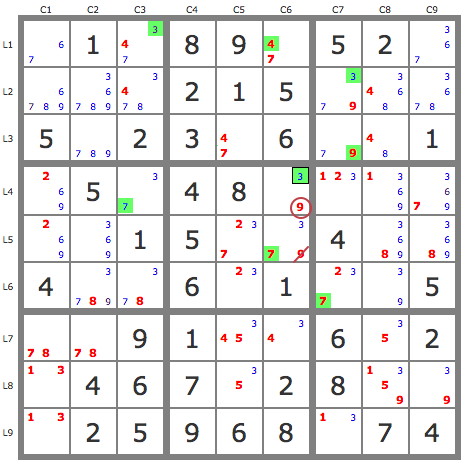 P'(7L3C5) : -7L3C5->4L3C5->4L1C3->3L1C9->6L1C1->2L4C1->2L6C7->3L6C5->7L5C6 => -7L1C6, -7L5C5 => L3C5=7
P'(7L3C5) : -7L3C5->4L3C5->4L1C3->3L1C9->6L1C1->2L4C1->2L6C7->3L6C5->7L5C6 => -7L1C6, -7L5C5 => L3C5=7
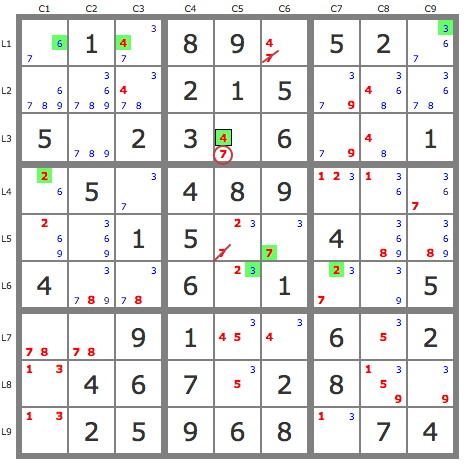
 En savoir plus ...
En savoir plus ...




