S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -660Grille de niveau 11 conventionnel.
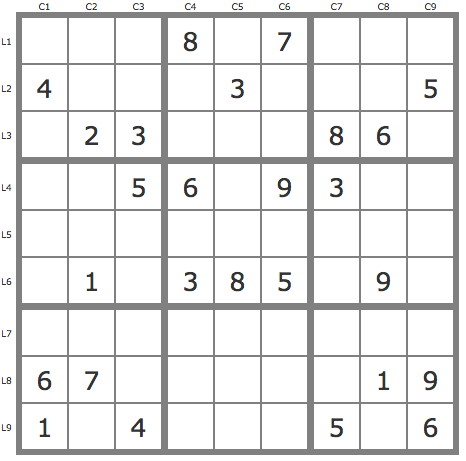
Commentaires sur cette grille
De Phidippides
(Publié le 20/02/2020)
Le dévoilé 5 en (6,6) peut être enlevé pour former une grille minimale mais pas plus difficile.
De Robert Mauriès
(Publié le 20/02/2020)
@ Phidippides : Merci pour cette information. Mais il serait utile aussi que vous donniez votre résolution, toute résolution étant intéressante à connaître et analyser. Cordialement Robert
De Robert Mauriès
(Publié le 20/02/2020)
Voici trois petits théorèmes parfois utiles dans la résolution pas à pas d'une grille : Si deux anti-pistes P'(E1) et P'(E2) sont opposées, tout candidat C qui voit E1 et E2 peut être éliminé. Sa démonstration est très simple. Ce théorème est à rapprocher du suivant tout aussi simple à démontrer : Si un candidat C voit un ensemble E et P'(E), C peut être éliminé. Le troisième théorème s'apparente à celui des pistes conjuguées bien que les deux anti-pistes considérées ne soient pas, à priori, conjuguées. E1 et E2 étant deux sous-ensembles disjoints d'une même entité : - tout candidat qui voit à la fois un candidat de P'(E1) et un candidats de P'(E2) peut être éliminé. - tout candidat commun à P'(E1) et P'(E2) est un candidat solution de sa case. Dans cette grille 660, vous pouvez appliquer ces théorèmes, par exemple pour éliminer les 2L8C45 avec comme conséquence le placement du 2L8C7. Dans la recherche de l'unicité de la solution seuls les théorèmes 2 et 3 sont utilisables.
De Paolo
(Publié le 20/02/2020)
Bonsoir 1) 5 placements par les TB initiales. P(1L3C9)=>couvre la grille 2)P(4L3C9)=>contradiction 3)P(7L3C9)=>contradiction=>solution.
De François C.
(Publié le 21/02/2020)
Bonjour, Les TB donnent 5 placements + 3 alignements. Il y a alors 23 paires de candidats non équivalentes, mais j’en ai trouvé une seule qui mène à une taille 2 : c’est 7L3C19 équivalente à 7B1. P(7L3C9) est invalide. Ensuite, pour éviter de retomber exactement sur la même résolution que Paolo, on peut utiliser la paire 17L4C5 qui mène à la solution par recouvrement des 2 pistes.
De Phidippides
(Publié le 22/02/2020)
@ Robert Mauriès : Comme j'ai un programme, je pourrais donner la meilleure solution sans me fatiguer, mais si je le faisais à chaque fois, je ne suis pas sûr que les autres joueurs seraient contents. C'est pour cela que je me suis abstenu.
De Robert Mauriès
(Publié le 22/02/2020)
@ Phidippides : Au contraire, faites nous profiter des meilleurs résolutions que votre programme donne, au moins de temps en temps. Robert
De François C.
(Publié le 22/02/2020)
@ Phidippides : Bonsoir, moi aussi j'ai fait un programme et ça ne m'empêche pas de donner mes solutions. Je pense que beaucoup parmi ceux que j’ai vu défiler sur ce forum depuis 2 ans ont une assistance informatique plus ou moins avancée.
De Francis Labetoulle
(Publié le 23/02/2020)
Bonjour Sauf erreurs les trois 7 de C3 permettent une résolution de taille 2?
De François C.
(Publié le 23/02/2020)
@ Francis Labetoulle : Bonsoir, C’est exact mais il s’agit d’un triplet. Je faisais simplement remarquer dans mon premier message qu’il n’y a qu’une seule paire sur 23 qui permet d’obtenir une taille 2.
De Francis Labetoulle
(Publié le 24/02/2020)
@ François C : Bonjour J'ai proposé cette résolution sans esprit de contradiction, bien content de l'avoir obtenue par voie "quasi méthodologique". D'ailleurs Robert peut y observer des aspects intéressants concernant les croisements des pistes (aux choix...) Pour ces grilles de niveau "modeste" on peut espérer s'approcher d'une résolution niveau TDP sans programme. Il en est bien sûr tout autrement pour les grilles très difficiles et c'est là que vos programmes seraient très utiles, de mon point de vue... Les cheminements associés sont toujours très instructifs. Grand merci de nous les faire connaître.
De François C.
(Publié le 28/02/2020)
@ Robert Mauriès : Bonjour, Je pense que le 3ème théorème que vous citez n’apporte rien parce que si j’appelle E l’entité et que je pose : E = E1 U E2 U E3 (3 sous-ensembles disjoints et E3 éventuellement vide) F1 = E – E1 = E2 U E3 F2 = E – E2 = E1 U E3 alors P’(E1) = P(F1) et P’(E2) = P(F2), et comme F1 U F2 = E, les pistes P(F1) et P(F2) sont conjuguées. Donc ce théorème revient à appliquer 2 propriétés connues de ces pistes conjuguées. De plus le cas où E3 n’est pas vide n’apporte rien, bien au contraire, car il serait plus efficace de considérer par exemple les 2 pistes conjuguées P(F1) et P(E1) car P(E1) contient P(E1 U E3) = P(F2).
De Robert Mauriès
(Publié le 28/02/2020)
@ François C : D'accord avec vous, mon propos s'adresse à qui voudrait utiliser uniquement des anti-pistes. Mais vous venez de donner une démonstration élégante de ce théorème en partant des pistes conjuguées.
Ajouter un commentaire
La solution
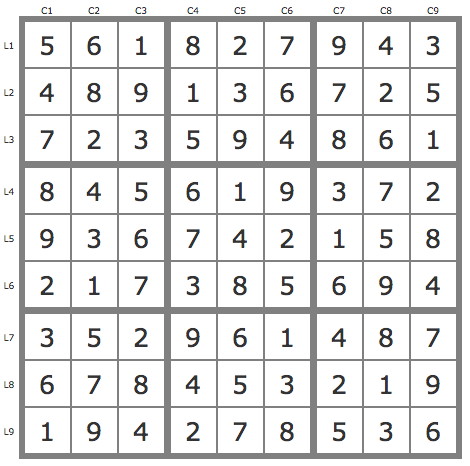
 En savoir plus ...
En savoir plus ...




