S'identifier S'inscrire
assistant-sudoku.com
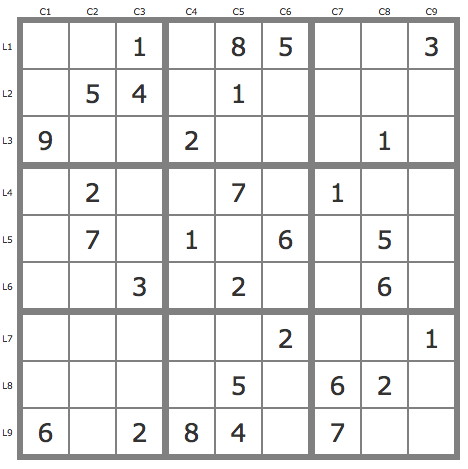
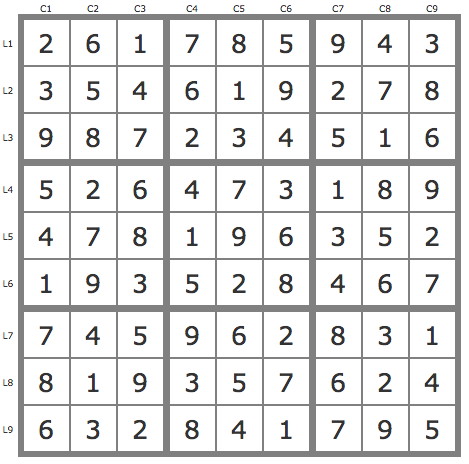
Grille Sudoku résolue
La grille -657Grille de niveau 11 conventionnel.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 30/01/2020)
Pas de commentaire pour l'instant.
De Phidippides
(Publié le 30/01/2020)
Pour avoir la grille minimale, il faut enlever les dévoilés suivants : 1L1C3, 1L2C5, 2L7C6 et 2L9C3 et on obtient une grille de difficulté moyenne (environ 15)
De Robert Mauriès
(Publié le 30/01/2020)
@ Phidippides : Bonsoir ! Comment déterminez-vous la grille minimale ? Robert
De Paolo
(Publié le 30/01/2020)
Bonsoir 1) 6 placements par les TB initiales. P(3L4C6)=> couvre la grille 2)P(3L4C4)=> contradiction 3)P(3L4C8)=>contradiction=>solution. ou P(6L3C9)=> couvre la grille 1) 6 placements par les TB initiales. 2)P(4L3C9)=> contradiction 3)P(8L3C9)=>contradiction=>solution.
De Phidippides
(Publié le 31/01/2020)
@ Robert Mauriès : Bonjour Robert C'est mon esclave qui le calcule. Avez-vous changé d'adresse courriel ? Je vous ai envoyé quelques grilles produites par mon générateur sans réponse. P.S. esclave = mon programme de sudoku
De Robert Mauriès
(Publié le 31/01/2020)
@ Phidippides : Bonsoir. Non je n'ai pas changé d'adresse mail. Je ne vous ai pas encore répondu car je suis très occupé, mais je le ferai. Cordialement Robert
De François C.
(Publié le 01/02/2020)
Bonjour, Voici une résolution qui utilise comme TB, à tous les niveaux, uniquement les candidats uniques (en case ou zone) : Les TB => 6 placements P(3L5C5) => contradiction => 3L5C5 suppr Les TB => 13 placements P(3L3C6) => contradiction => 3L3C6 suppr Les TB => solution. N.B: les résolutions de Paolo fonctionnent aussi avec ce minimum de TB.
De Claude Renault
(Publié le 01/02/2020)
6 placements par procédures de base : P(9L5C3) invalide ; P(8L5C3).P(3L5C5) invalide ; P(8L5C3).P(9L5C5) solution
Ajouter un commentaire
La solution
Après réduction de la grille par les TB, résolution pas à pas avec les TB.
1) JP(9C3)
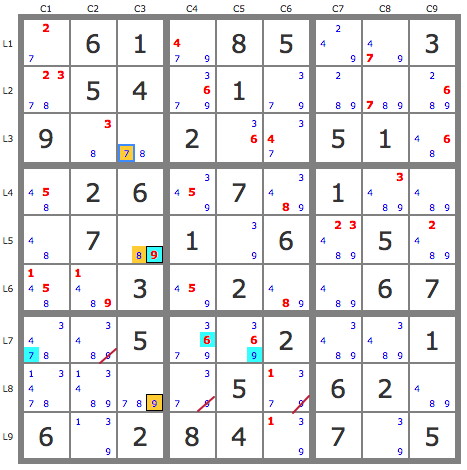 2) JP(39L5C5)
2) JP(39L5C5)
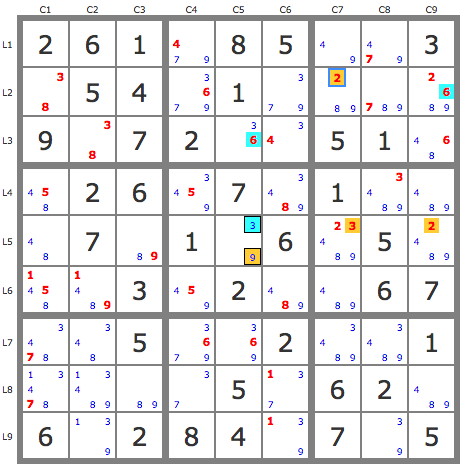 3) JP(9B4)
3) JP(9B4)
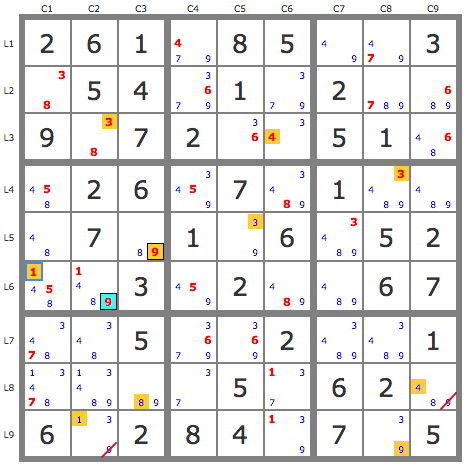 4) JP(48L1C5)
4) JP(48L1C5)
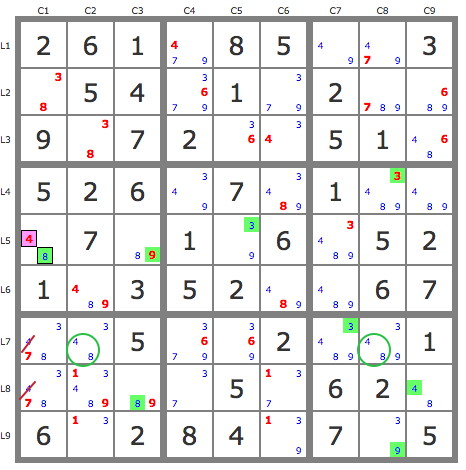 5) JP (48L8C9) qui valide 4L7C2 et la grille ce termine par les TB.
5) JP (48L8C9) qui valide 4L7C2 et la grille ce termine par les TB.
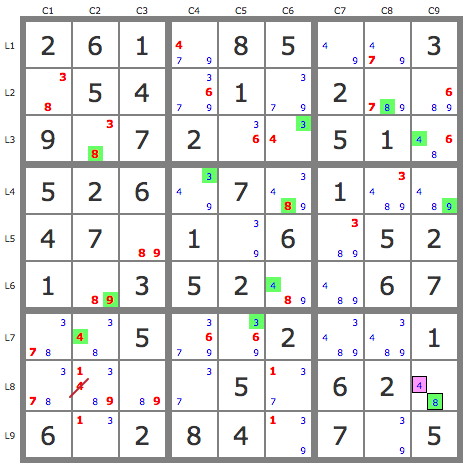
 En savoir plus ...
En savoir plus ...




