S'identifier           S'inscrire

assistant-sudoku.com

Grille Sudoku résolue

La grille -647
Grille de niveau 10 conventionnel.



Afficher les commentaires


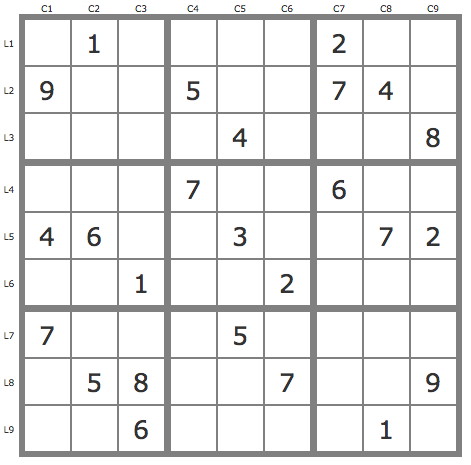
Commentaires sur cette grille

De Paolo
(Publié le 21/12/2019)

Bonsoir, 8 placements par les TB initiales. Résolution par croisement de deux pistes conjuguées P (1L3C7) et P (1L5C7).

De Robert Mauriès
(Publié le 23/12/2019)

Belle résolution Paolo, dans la plus traditionnelle des démarches de TDP. Voici une autre manière de résoudre utilisant des anti-pistes : P'(6r6c4)={6L5C5, 2L8C5, 1L2C5, 1L4C8, 4L6C79,...} => -4L6C4, soit L4C6=4 + 3 placements. P'(3L4C9)={1L4C9, 1L2C5, 2L2C3, 3L3C2,... } => -3L4C2, soit L4C2=2 et résolution de la grille par induction (candidats uniques). J'ai utilisé pour cela le théorème suivant : Si B voit A et un candidat de P'(A), B peut être éliminé.


Ajouter un commentaire

Adresse Mail

Mot secret (Mot secret oublié)
Celui utilisé pour archiver, ou si vous n'avez jamais archivé, un mot secret de votre choix
Prénom et/ou Nom

Pour la sécurité du site,
merci de saisir les lettres et chiffres situés dans ce code : 2+BY*2-*/b

Commentaire


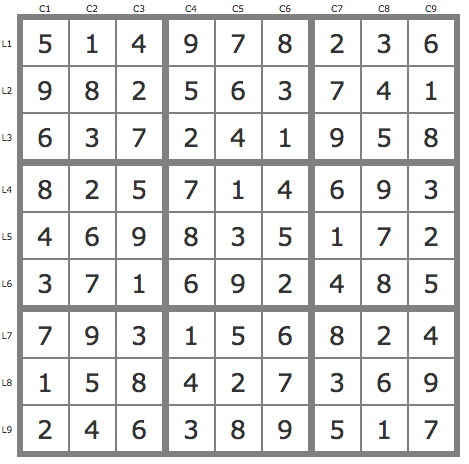
La solution

Après réduction de la grille par les TB (8 placements), voici une manière de résoudre utilisant des anti-pistes : P'(6r6c4)={6L5C5, 2L8C5, 1L2C5, 1L4C8, 4L6C79,...} => -4L6C4, soit L4C6=4 + 3 placements. P'(3L4C9)={1L4C9, 1L2C5, 2L2C3, 3L3C2,... } => -3L4C2, soit L4C2=2 et résolution de la grille par induction (candidats uniques). J'ai utilisé pour cela le théorème suivant : Si B voit A et un candidat de P'(A), B peut être éliminé.



assistant-sudoku.com est la propriété de Robert Mauriès (assistant.sudoku(AT)free.fr). Toute reproduction interdite sans son autorisation.