S'identifier S'inscrire
assistant-sudoku.com
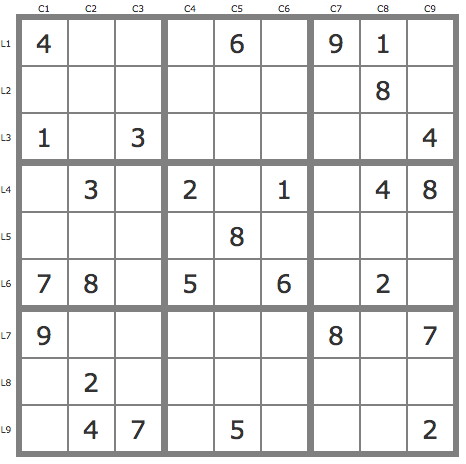
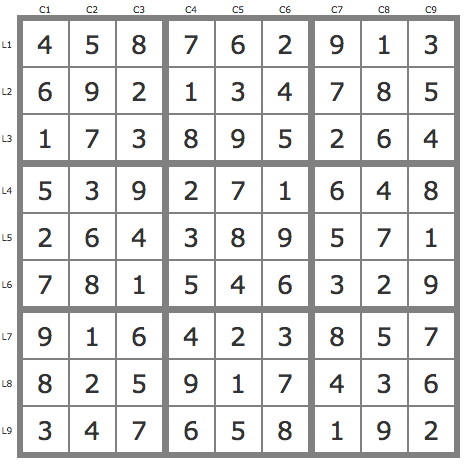
Grille Sudoku résolue
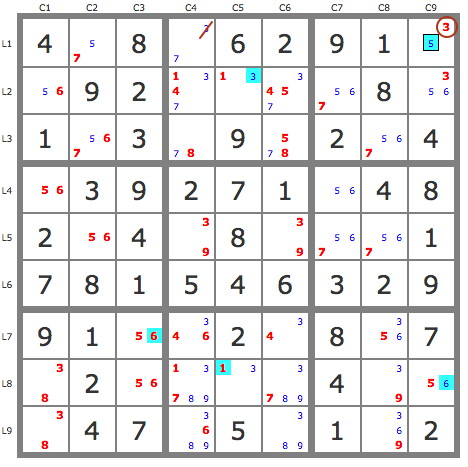
La grille -645Grille de niveau 10/11 conventionnel.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 12/12/2019)
Pas de commentaire pour l'instant.
De François C.
(Publié le 13/12/2019)
@ Robert Mauriès : Bonsoir, Voici une résolution garantie sans contradiction :-). 1) Les TB => 4L8C7, 8L1C3, 2L1C6, 2L3C7, 2L7C5 ensuite la paire 79C5 permet d’éliminer 5 candidats et la paire cachée 38B7 d’en éliminer 3. 2) Jeu de pistes à partir de 13L6C7 : P(1L6C7) = {1L9C4, 3L8C5, 4L6C5*, 4L5C3*, 2L5C1*, 2L2C3*…} P(3L6C7) = {4L6C5*, 4L5C3*, 2L5C1*, 2L2C3*…} Les 4 candidats repérés par * sont communs aux 2 pistes et sont donc validés. 3) Les TB => 3 intersections ligne(ou colonne) / bloc : 3L6, 9C3, 3C8 => 6 candidats supprimés. 4) Jeu de pistes à partir de 6L3 : P(6L3C2) ={9L2C2*, 5L2C1, 6L4C1, 5L3C6, 7L3C8, 9L3C5*, 7L4C5*, 5L4C7, 9L4C3*…} P(6L3C8) = {7L5C8, 7L4C5*, 9L3C5*, 9L2C2*, 6L2C1, 5L4C1, 6L4C7, 9L4C3*…} Les 4 candidats repérés par * sont communs aux 2 pistes et sont donc validés. De plus le 5L3C8 et le 5L5C8 peuvent être éliminés car ils voient chacun les 2 pistes en même temps. 5) Les TB => 1L6C3, 3L6C7, 9L6C9, 1L7C2 6) P(6L3C2) peut être prolongée avec {6L5C8, 1L5C9*} et P(6L3C8) peut être prolongée avec {1L9C7, 1L5C9*}. Donc on valide le 1L5C9 et la grille se résout avec les TB. Francois
Ajouter un commentaire
La solution
Après réduction de la grille par les TB (5 placements), on exploite les paires 1B9, 7B3, 5B4, et 4B2, avec des jeux de pistes conjuguées successifs.
Mais on peut aussi utiliser le théorème suivant :
"Si un candidat C voit un candidat A et un candidat contenu dans P'(A), C peut être éliminé".
1) P'(3r6c7) = {1r6c7, 1r8c9, 3r8c5, 4r6c5,...} => -3r6c5 => r6c5=4 + 3 placements par les TB.
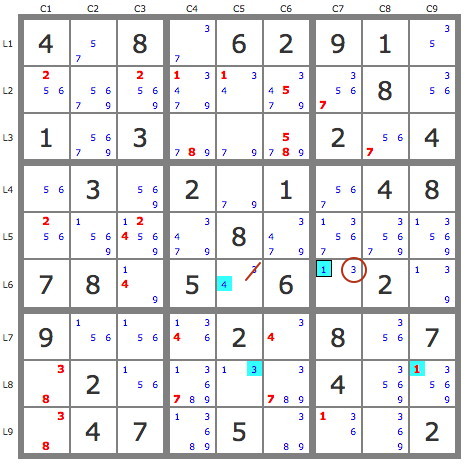 2) P'(7r3c8) = {7r2c7, 7r4c5, 9r3c5, ...} => -7r3c5 => r3c5=9 et 7 placements par les TB.
2) P'(7r3c8) = {7r2c7, 7r4c5, 9r3c5, ...} => -7r3c5 => r3c5=9 et 7 placements par les TB.
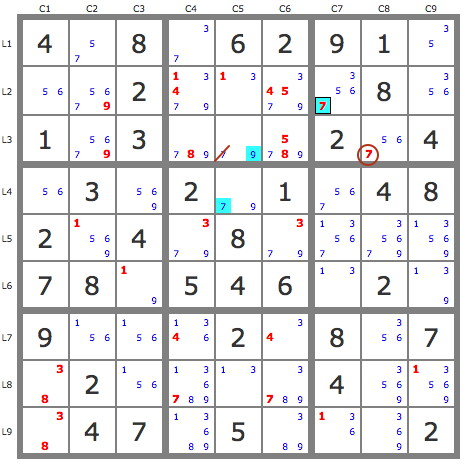 3) P'(6r4c7) = {5r4c7, 5r2c1, 5r1c9, 3r2c9, 6r3c2, 6r2c7, 1r9c7,...} => -6r9c7 => r9c7=1 et r5c9=1.
3) P'(6r4c7) = {5r4c7, 5r2c1, 5r1c9, 3r2c9, 6r3c2, 6r2c7, 1r9c7,...} => -6r9c7 => r9c7=1 et r5c9=1.
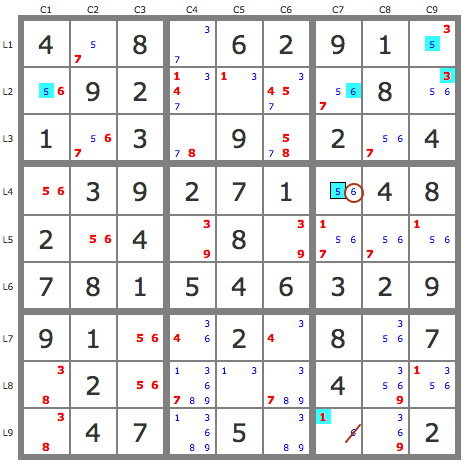 4) P'(3r1c9) = {5r1c9, 6r8c9, 6r7c3, 34r7c46, 1r8c5, 3r2c5, ...} => -3r1c4 => r1c4=7, et fin de la grille par les TB
4) P'(3r1c9) = {5r1c9, 6r8c9, 6r7c3, 34r7c46, 1r8c5, 3r2c5, ...} => -3r1c4 => r1c4=7, et fin de la grille par les TB
 En savoir plus ...
En savoir plus ...




