S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
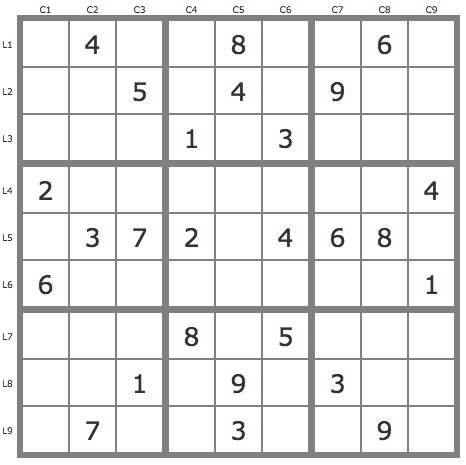
La grille -644Grille de niveau 12/13 conventionnel.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 05/12/2019)
Pas de commentaire pour l'instant.
De Paolo
(Publié le 06/12/2019)
Bonjour 1) 2 placements par les TB initiales. P(5L5C5) => couvre la grille 2) P(1L5C5).P(2L1C3)=> contradiction 3) P(1L5C5).P(3L1C3=>contradiction=>solution.
De François C.
(Publié le 06/12/2019)
Bonsoir, Les TB donnent 2 placements, 2 alignements et un triplet (467C4). Ensuite l’entité 1B1 est très efficace puisque : P(1L1C1) et P(1L2C1) sont invalides. P(1L2C2) = solution.
De Claude Renault
(Publié le 08/12/2019)
placements par procédures de base : 2 P(7L2C1) invalide P(7L1C1).P(2L1C3) solution ; P(7L1C1).P(3L1C3) invalide
De Robert Mauriès
(Publié le 11/12/2019)
A l'attention de ceux qui souhaitent résoudre une grille sans faire appel directement à la notion de contradiction (piste invalide), voici un théorème qui les aidera dans une résolution étape par étape. "Si un candidat C voit un candidat A et voit un candidat B appartenant P'(A), C peut être éliminé". La grille 644 a été résolue de cette manière afin de vous donner un exemple d'utilisation de théorème (Cliquez sur "Voir la résolution" ci-dessus).
Ajouter un commentaire
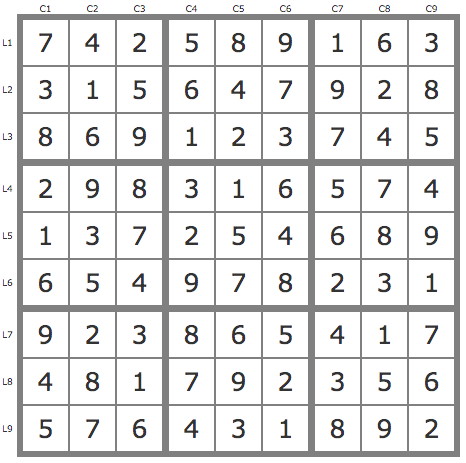
La solution
On peut faire une résolution rapide dès lors qu'on accepte le principe de la contradiction, par exemple avec les 1b1 voir forum).
Voici une résolution avec des chaînes courtes utilisant les pistes conjuguées et le théorème suivant :
"Si un candidat C voit un candidat A et voit un candidat B appartenant à P'(A), C peut être éliminé".
1) P'(1r5c5) = {1r5c1, 1r2c2, 1r7c8, 1r9c6, ...} => -1r4c6 => r9c6=1.
2) P'(2r1c3) = {3r1c3, 3r7c1, 3r2c9, 9r3c1, 8r3c79, 26r3c23, ...} => -2r2c2
3) P'(5r8c2) = {5r89c1, 1r5c1, 1r2c2, 1r4c4, 6r3c23, 6r7c5, 2r8c6, ...} => -2r8c2
=> X-wing 2c2c5 (ou JP(2c2)) => -2r3c3, -2r3c789, -2r7c3, -2r7c789
4) P'(7r7c5).P(2r7c5) = {2r7c5, 2r9c3, 3r1c3, 69r7c23, 7r7c9, ...} et P'(7r7c5).P(6r7c5) = {6r7c5, 7r7c9, ...} => -7r7c78 => -4r7c1 -4r8c8, -4r9c7
5) P(6r4c6) = {6r4c6, 8r6c6, ...} et P(6r4c5) = {6r4c5, 1r5c5, 5r5c1, 48r89c1, ...} que l'on développe par une extension :
P(6r4c5).P(2r9c3) = {..., 2r9c3, 3r1c3, 3r2c9, 8r3c79, 8r2c2, 8r6c6, ...}
P(6r4c5).P(6r9c3) = {..., 6r9c3, 4r9c4, 8r9c1, 8r8c9, 8r3c7, 8r2c2, 8r6c6, ... }
=> r6c6=8
6) P(2r1c3) = {2r1c3, 2r3c5, 2r7c2, 3r7C3,...} et P(3r1c3) = {3r1c3, 3r2c9, 3r7c1, 9r3c1, 8r2c79, 6r3c3, 9r7c3...}
= > -6r7c3, -9r7c2 et -6r3c5 => -6r2c2
7) P(9r6c2) = {5r6c2, 1r5c1, 1r4c5, 6r7c5, 2r7c2, 4r9c4, 5r9c1,..., 7r6c5, 2r6c7, 8r9c7, 6r9c3, 6r3c2, ...}
=> -9r3c2 => r4c3=8, -6r8c2, -8r3c2
8) P(1r5c5) = {1r5c5, 5r5c1, 5r8c2, ...} et P(5r5c5) = {5r5c5, 7r6c5, 2r3c5, 2r8c6, ..., 7r7c9, 5r8c8, ...}
=> -5r8c19
9) P'(9r1c6) = {9r1c4, 5r3c5, 1r5c5, 5r5c1, 5r8c2, ..., 7r6c5, 7r7c9, 8r3c9, 8r9c7, 4r9c1, 6r9c4, 7r2c4, ...} => -7r1c6
10) P(5r3c8)={5r3c8, 5r1c4, 9r1c6, ...}, P(5r8c8) = {5r8c8, 5r9c1, 5r5c5, 5r1c4, 9r1c6, ...} et
P(5r46c8) = {5r46c8, 2r6c7, 7r6c5, 7r7c9, 2r8c8, 2r7c5, 2r9c3, 3r1c3, 3r2c9, 2r1c9, ...} => -2r1c6
=> r1c6= 9, r1c4=5
Note : on a ici volontairement évité l'utilisation du UR35r46c48 permettant d'arriver plus rapidement au même résultat, ceci afin de préserver la preuve de l'unicité de la solution.
11) P(2r1c3) = {2r1c3, 6r9c3, 4r9c4, ...} et P(2r3c2) = {2r3c2, 2r2c6, 6r2c4, 4r9c4,...} => r9c4=4 =>r8c1=4
12) P(5r9c1) = {5r9c1, 1r5c1, 1r2c2, ...} et P(8r9c1) = {8r9c1, 8r2c2, 257r469c7, 1r1c7, 1r2c1, ...} => -1r2c8
=> r1c7=1, r7c7=4, r7c8=1, r3c8=4, -7r2c19, -2r2c9
Mais aussi
P(5r9c1) = {5r9c1, 1r5c1, 5r5c5, 7r6c5, ...} et P(8r9c1) = {8r9c1, 5r8c2, 8r3c7, 5r3c9, 5r9c7, 7r4c7,...} => -5r9c9 , -7r6c78 => r6c5=7 et fin avec les TB.
 En savoir plus ...
En savoir plus ...




