S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
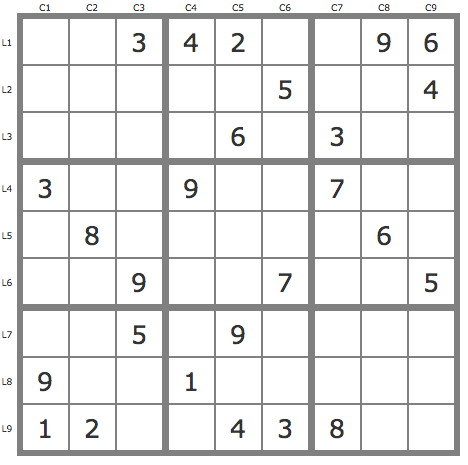
La grille -630Grille à solutions multiples : combien de solutions compte-t-elle et lesquelles ?
Commentaires sur cette grille
De Robert Mauriès
(Publié le 28/07/2019)
Indication : paire 67L9C3 et 3 solutions.
De Francis Labetoulle
(Publié le 28/07/2019)
Bonjour Avec la case L9C4 P(5L9C4).P(6L7C4) =1; P(5L9C4).P(6L8C6) = 1; P(6L9C4) = 1; P(7L9C4) = 0, donc 3 solutions. Que peut-on déduire du tracé de l'arbre de résolution pour une telle grille?
De Paolo
(Publié le 28/07/2019)
Bonjour, 1) 4 placements par les TB initiales. P(1L4C2)=> couvre la grille=S1 P(6L4C2)=> couvre la grille=S2 2)P(4L4C2)=> contradiction P(7L9C3)=> couvre la grille=S3 3)P(5L4C2).P(6L9C3)=> contradiction=> solution
De Robert Mauriès
(Publié le 29/07/2019)
@ Francis Labetoulle : Bonjour Francis. La notion d'arbre de résolution basée sur le développement par des extensions en cascade de deux pistes conjuguées reste la même pour les grilles à solutions multiples que pour les grilles à solution unique, à ceci près que dans le second cas une seule cascade conduit à la solution (voir théorie des pistes ci-contre) alors que dans le premier cas plusieurs cascades conduisent aux diverses solutions. Je vois là d'ailleurs un lien avec le débat actuel hors forum sur P(E) où la notion de piste multiforme (qu'elle soit valide ou invalide) se discute.
De Francis Labetoulle
(Publié le 29/07/2019)
@ Robert Mauriès : Bonjour Robert Merci pour votre réponse. Je me demandais également si l'utilisation d'un arbre de résolution pouvait aider dans les discussions actuelles. Par ailleurs la notion de taille et à fortiori celle de niveauTDP n'ont semble-t-il, pas de signification pour une grille à solutions multiples, bien que les cheminements proposés puissent présenter des nombres distincts de "ramifications". Ce point de vue est-il correct, et si oui pourquoi ne pas envisager une généralisation (aisée?) du calcul de la taille associée à un arbre de résolution donné?
De Robert Mauriès
(Publié le 29/07/2019)
@ Francis Labetoulle : Re bonjour FRancis. La notion de taille de résolution, donc celle de niveau TDP, qui est en réalité la taille de l'arbre de résolution me semble rester valable pour les grilles à solutions multiples pour peu que chaque solution compte pour 1 dans le décompte. Ainsi pour cette grille le niveau TDP est de 4 au maximum.
De Francis Labetoulle
(Publié le 03/08/2019)
Bonjour à tous En cette période estivale, et pour aborder un sujet différent, je crois avoir constaté, sur l'exemple des grilles de top-sudoku niveau extrême, qu'il peut exister (au moins) un cheminement systématique menant à la solution, supposée unique, pour certain(s) générateur(s) de grilles. Peut-être suis-je en train d'enfoncer une porte ouverte mais, pour ceux qui, comme moi découvriraient cet aspect, je propose de choisir une grille de niveau élevé et de partir de la case à 3 candidats dont 2 sont liés à d'autres par lien forts (en rouge sur le logiciel de Robert). On s'apercevra que pour au moins 1 candidat il apparaît deux paires cachées dans la grille, à exploiter au mieux. Je vous laisse poursuivre... À signaler que le AI Escargot mentionné ci-contre peut se résoudre ainsi. Bien sûr il peut exister des cas avec 2 cases à 3 candidats semblables à celle mentionnée. Il faut faire alors le bon choix, avec un peu d'habitude. Si cette propriété, que j'ai vérifiée sur bon nombre de cas, est correcte, il reste si possible à l'expliquer à partir du mode de conception de ces grilles et là je manque presque totalement d'informations. Je suis preneur de tout renseignement sur le sujet. Bonnes vacances à tous!
De Robert Mauriès
(Publié le 04/08/2019)
@ Francis Labetoulle : Bonjour Francis. J'étudierai avec attention votre remarque sur les grilles de Top-Sudoku. Pour ma part j'ai remarqué que ces grilles extrêmes sont très souvent constituées de la même manière : 8 blocs de 3 dévoilés et 1 bloc de 2 dévoilés, ou 6 blocs de 3 dévoilés, 1 bloc de 2 dévoilés, 1 bloc sans dévoilé et 1 bloc de 4 dévoilés. J'ai constaté aussi (avec François) que certaines n'étaient que AI Escargot transformé (permutations). Il est donc possible que le générateur démarre avec un schéma donné et non aléatoire de dévoilés, et utilise des transformations (similitudes, permutations, rotations, etc...) pour générer plusieurs grilles (apparemment différentes) sur la base d'une même grille initiale.
De Paolo
(Publié le 12/08/2019)
@ Robert Mauriès et Francis Labetoulle : Bonjour. Je tiens à souligner la discussion intéressante sur la résolution des grilles de haut-sudoku niveau extrême entreprise dans le forum http://foruma .enjoysudoku.com/sk-and-related-loops-t35883.html sur le thème "SK et boucles associées" de Philip Beeby.l’extension des boucles "Presque Sk (+1) (+ 2) et (+3)" conduit à la résolution de presque tous les sudokos extrêmes. L'Escargot est également résolu avec cette technique. La résolution de l'escargot réalisée avec http://www.philsfolly.net.au/ Almost (+3) SK loop detected (red cells): (13=48)r3c56 - (48=159)r12c4 - (159=27)r56c4 - (27=16)r4c56 - (16=478)r4c89 - (478=16)r56c7 - (16=247)r12c7 - (247=13)r3c89 - loop No contradiction when 9 at r8c4 is true, 7 at r2c8 is true, and 4 at r5c8 is true and and others are all false Eliminations (green cells): r7c4 <> 5, r7c4 <> 9, r8c4 <> 5, r9c4 <> 1, r9c4 <> 5, r9c4 <> 9, r7c7 <> 6, r8c7 <> 6, r1c5 <> 4, r1c9 <> 4, r2c8 <> 4, r6c5 <> 7, r5c8 <> 7, r6c8 <> 7, r6c8 <> 8 Il est intéressant de noter que sur la technique "Almost Sk loops", il admet lui-même qu'il n'avait pas la démonstration théorique de la méthode et qu'il cherchait quelqu'un qui pourrait l'aider à découvrir le cadre théorique de la méthode. “IWould be delighted if someone could discover a theoretic frame work to astablish this approach to be valid”.
Ajouter un commentaire
La solution
Après réduction de la grille par les TB (4 placements), on exploite la paire 67L9C3.
- P(7L9C3) couvre la grille -> une solution.
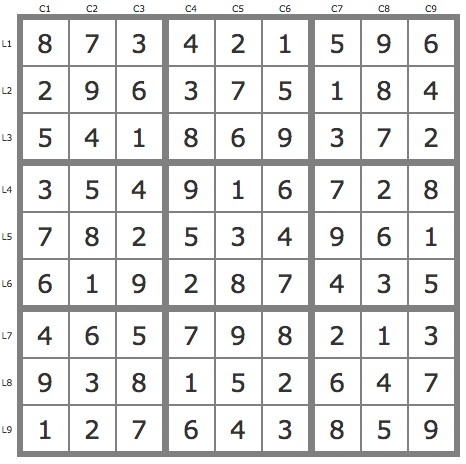 - P(6L9C3).P(6L4C2) couvre a grille -> une solution.
- P(6L9C3).P(6L4C2) couvre a grille -> une solution.
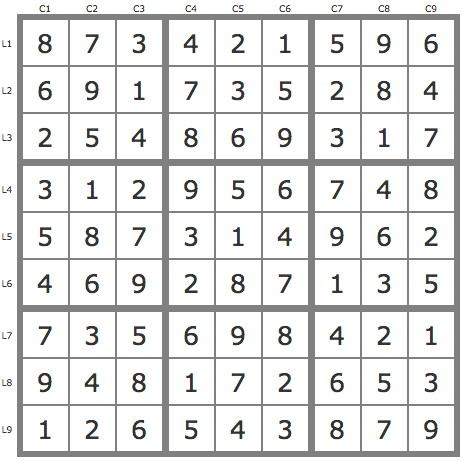
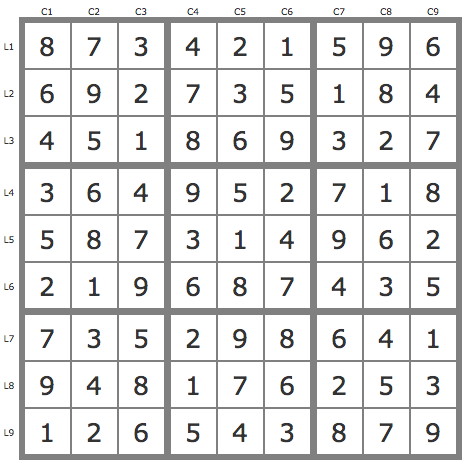 - P(6L9C3).P(6L6C2).P(5B8) couvre la grille -> une solution avec P(6L9C3).P(6L6C2).P(5L9C4) solution et P(6L9C3).P(6L6C2).P(5L8C5) invalide.
- P(6L9C3).P(6L6C2).P(5B8) couvre la grille -> une solution avec P(6L9C3).P(6L6C2).P(5L9C4) solution et P(6L9C3).P(6L6C2).P(5L8C5) invalide.
 En savoir plus ...
En savoir plus ...




