S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -618Grille de niveau 12 conventionnel à solution unique.
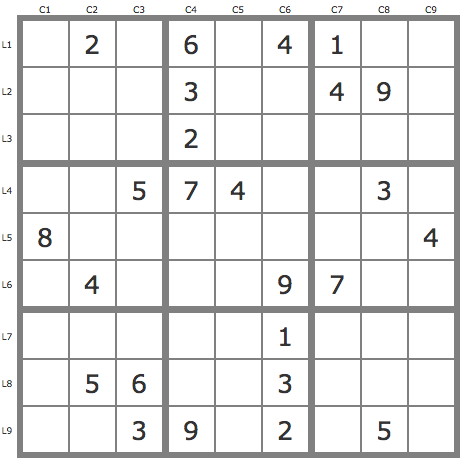
Commentaires sur cette grille
De Paolo
(Publié le 27/05/2019)
Bonjour, 3 placements par le TB initiales. P(2L6C3)=>couvre la grille P(1L6C3)=>invalide =>solution. ou 3 placements par le TB initiales. P(1L89C9)=>couvre la grille P(1L8C8)=>invalide =>solution.
De François C.
(Publié le 27/05/2019)
Les TB donnent 3 placements, 4 alignements et une paire. La première case contenant une paire de candidats est L1C8. Malheureusement la piste P(7L1C8) ne se développe pas du tout. Je passe donc à prochaine case contenant une paire de candidats : L4C6. P(6) se développe bien et P(8) aboutit à une contradiction. Je valide donc les 16 candidats de P(6). La première case avec une paire qui se présente est maintenant L1C3. P(8) couvre la grille. De plus P(9) aboutit à une contradiction ce qui prouve l’unicité de la solution.
De Francis Labetoulle
(Publié le 28/05/2019)
Bonjour 3 placements, 4 alignements et 1 quadruplet en B5. P(2L4C7) couvre la grille alors que P(2L4C1) est invalide donc taille 1 et unicité. La première piste fait apparaître un beau triplet caché 156 en L5 qui permet de développer cette piste. Déterrons un vieux problème, histoire de susciter une réponse : peut- on dire que les deux pistes se croisent suffisamment pour couvrir la grille, ou que c'est une "évidence" puisque l'une des pistes est invalide?
De Robert Mauriès
(Publié le 28/05/2019)
@ Francis Labetoulle : Bonjour Francis, bonjour à tous. C'est en effet une question qui a fait l'objet de discussions (en son temps) que de savoir si les interactions (validations et éliminations) de deux pistes suffit pour résoudre dans le cas d'un jeu de pistes composé d'une piste couvrant la grille et d'une piste invalide. La réponse est oui et non ! - Oui, car une piste invalide passe par tous les candidats de la grille, elle passe donc aussi par les candidats de la piste valide. Encore faut-il pousser le développement de la piste invalide au delà de sa restriction (restriction = ensemble des candidats de la piste que l'on peut placer à raison d'un seul candidat par entité) sans tenir compte de ses contradictions, ce que l'on ne fait pas en pratique généralement. - Non, car en pratique on arrête le développement d'une piste invalide à sa restriction et que dans ce cas rien n'indique que les interactions seront suffisantes. Des contre-exemples existent.
De Paolo
(Publié le 29/05/2019)
@ Robert Mauriès Francis Labetoulle : Bonjour, Je pense que l’utilisation de la méthode du croisement de deux pistes conjuguées pour traiter la résolution d’une grille (en particulier celles avec une solution unique) est moins efficace que la recherche d’une invalidità pour deux raisons: La première est qu'une piste obtenue avec l'intersection de deux pistes conjuguées produit au plus le même résultat obtenu avec la démonstration de l'invalidité de l'une des deux pistes. Il est également peu logique d'utiliser le croisement. si la piste obtenue par croisement n'a pas le même résultat que l'invalidité de l'une des deux pistes. La deuxième raison est qu’il est beaucoup plus difficile d’obtenir une piste déterminée par un sous-ensemble commun aux deux pistes ayant le même résultat que la piste obtenue à partir de la validation de l’une des deux pistes conjuguées. Certes, il est possible d’obtenir une piste pour croisement même s’il n’est pas possible de démontrer l’invalidité de l’une des deux pistes mais le résultat obtenu peut conduire à l’élimination de candidats possibles mais il n’est certainement pas utile pour obtenir une résolution à taille minimale.
De Robert Mauriès
(Publié le 29/05/2019)
@ Paolo : Bonjour Paolo. Vous avez tout à fait raison, il est plus efficace de rechercher les invalidités que de rechercher les interactions, notamment si l'on dispose d'un logiciel qui aide à cela. Ce point de vue est indiscutable. Mais on est moins dans l'esprit de la TDP et on est un peu plus dans celui de la méthode "Essai-Erreur". En revanche, lorsqu'il s'agit de résoudre "à la main", donc sans l'aide d'un logiciel, la recherche des invalidités peut devenir fastidieuse. C'est pourquoi, pour ceux qui travaillent à la main (comme moi), je suggère de construire simultanément les deux pistes conjuguées, pas à pas, d'exploiter les interactions et si au cours de cette construction l'invalidité apparaît, alors tant mieux et il faut en profiter. On ne peut plus dire alors qu'on dans la méthode "Essai-Erreur" car le but n'était pas de rechercher l'invalidité.
De Francis Labetoulle
(Publié le 29/05/2019)
@ Paolo : Bonjour Paolo et bonjour à tous Ma question ouverte portait uniquement sur l'opportunité de mentionner que les croisements de deux pistes conjuguées dont l'une couvre la grille et l'autre est invalide, permettent, à eux-seuls d'obtenir la solution, si on considère que la piste invalide permettra d'obtenir ce résultat si on admet qu'elle puisse occuper plusieurs fois certaines cases. Robert a bien résumé le problème. Je suis d'accord avec vous concernant la grande efficacité de la recherche des pistes invalides, mais là encore Robert a bien traduit les états d'âme que l'on peut avoir à utiliser ce choix de résolution sans mettre en place des pistes conjuguées. En fait il est clair qu'on ne recherche que les pistes invalides dont les antipistes semblent prometteuses, et que la notion de piste conjuguée est implicite. J'avoue que je me pose toujours la question suivante : un grand nombre de méthodes dites expertes mettent en jeu la suppression d'un ou plusieurs candidats via l'usage (non mentionné ) de deux pistes conjuguées. Pourquoi ces théoriciens s'arrétent-ils à ce premier stade, sans exploiter plus avant ces pistes qu'ils semblent ignorer? En clair, la vraie question est: où se situerait la faute "logique" ou "de bon goût" à poursuivre la résolution dans cette voie? Je n'invoquerai pas ici l'opinion probable de ces puristes sur la recherche des pistes invalides. Je crois que cette question a pu poser un problème à certains parmi nous et je serais très intéressé de connaître leur point de vue.
De Paolo
(Publié le 29/05/2019)
@ Robert Mauriès : Bonjour Robert et bonjour à tous. Ce que vous dites n’est pas tout à fait convaincant car, que l’on résolve la grille "à la main" ou à l’aide d’un programme informatique ad hoc, la logique est toujours la même et seuls les temps de résolution sont correctement modifiés. Au moment où un joueur analyse deux pistes conjuguées P (E1) et P (E2) pour avancer dans la résolution d'une grille, il ne sait pas s'il parviendra à obtenir un résultat positif en croisementles deux pistes, mais ce qui est certain, c'est qu'avant de prouver que la piste valide obtenue à partir du sous-ensemble des deux pistes ne contient pas E1 ou E2, l'invalidité de l'une des deux pistes P (E1) ou P (E2) a déjà été démontrée. La conséquence en est que l'invalidité d'une des deux pistes implique la validité de la piste obtenue par croisement mais l'inverse n'est pas toujours vrai.
De Robert Mauriès
(Publié le 29/05/2019)
@ Francis Labetoulle : Bonjour Francis. Paolo répondra certainement à votre commentaire. Je voudrais seulement vous donner mon avis sur la question que vous vous posez toujours. Je crois que les différents théoriciens qui ont défini les techniques expertes étaient "enfermés" dans leurs quêtes de "recettes" toutes prêtes à l'usage des sudokistes, perdant de vue qu'une théorie globale était possible. S'ajoute à cela, comme vous le dites, que la recherche d'une invalidité liée au placement d'un candidat, qu'ils qualifient d'Essai-Erreur, n'est pas selon eux une technique experte. Ce faisant ils sont passés à côté de la notion de piste, de pistes conjuguées et d'antipiste. Je pense d'ailleurs qu'aux yeux de ces théoriciens bien pensant, la TDP n'est pas une technique de résolution "digne de ce nom" et qu'elle n'est qu'une technique de type "Essai-Erreur" ou "force brute". Sachez aussi que j'ai posé, en son temps, cette question à Berthier qui m'a répondu, de manière très lapidaire, que la TDP était une méthode récursive et qu'il ne s'intéressait pas aux aspects récursifs.
De Paolo
(Publié le 29/05/2019)
@ Francis Labetoulle : Bonjour Francis. Je pense que la plupart des méthodes de résolution utilisées pour résoudre un schema sont des méthodes permettant de trouver une contradiction. En fait, même les mêmes méthodes présentes dans la TB sont des méthodes dont les règles découlent de la recherche d’une contradiction. En règle générale, toute elimination individuelle obtenue avec une méthode experte peut être obtenue de manière égale en démontrant l'invalidité de la piste créée par ce candidat. Cela me fait penser que l'application de la TB dans l'hypothèse où un seul candidat est vrai est la méthode la plus puissante à utiliser. C'est un peu comme si on disait que la TB est l'algèbre de toute autre méthode experte. Si nous y réfléchissons chaque fois que nous démontrons un’invalidité, nous construisons une méthode d’expert ad hoc en appliquant un nombre N de TB qui n’est valable que pour cette élimination unique (c’est comme écrire une expression algébrique). Le fait important est que ceci est construit très simplement.
De Francis Labetoulle
(Publié le 30/05/2019)
@ Robert Mauriès et Paolo Bonjour et merci à tous deux pour vos réponses qui me confortent, si besoin était, dans l'application préférentielle de la technique des pistes. Pour compléter la réponse de Paolo j'ai effectivement observé dans de nombreux cas d'application de techniques expertes qu'il suffisait, avec usage des TB, de vérifier que la piste issue du candidat à éliminer était invalide. De manière complémentaire ce résultat pouvait aussi s'obtenir par usage de pistes conjuguées judicieusement choisies. Est-ce une vérité première? La réponse est probablement impossible. Il faudrait "piocher" du côté des braids et whips de Denis Berthier en particulier pour étoffer ce point de vue. Le commentaire de Robert est sans équivoque ! J'ai quelques idées d'interprétation du terme récursivité, lequel n'a rien de péjoratif en programmation fonctionnelle. A t-il un lien avec avec la possibilité de construite des pistes en cascade en nombre fini, jusqu'à conclusions? Bonne fin de semaine
De Robert Mauriès
(Publié le 30/05/2019)
@ Francis Labetoulle et Paolo : Paolo à raison, nous pourrions développer une technique universelle sur le seul principe du raisonnement par l'absurde qui conduit à contradiction, à savoir : si ce candidat est placé dans cette case, la règle du sudoku n'est plus respectée, donc ce candidat ne peut pas être placé dans cette case. Toutes les techniques sont établies sur ce principe. Mais ce serait un peu fastidieux en pratique de procéder constamment de la sorte, aussi est-il utile d'avoir établi comme des règles résultants de ce raisonnement par l'absurde ce qu'on appelle les TB. C'est le fondement même de la TDP, il n'est pas utile d'aller plus loin en construisant d'autres règles (expertes), une seule suffit, celle des pistes conjuguées avec les notions de pistes valides et invalides, en utilisant les TB. Sur la récursivité, je réponds à Francis que oui la récursivité a un lien avec le fait que la solution est atteinte par des pistes en cascade qui, en raison du nombre fini de cases et de candidats, sont en nombre fini. C'est me semble-t-il le principe et la conséquence de la récursivité. Bonne journée à tous.
Ajouter un commentaire
La solution
 En savoir plus ...
En savoir plus ...




