S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
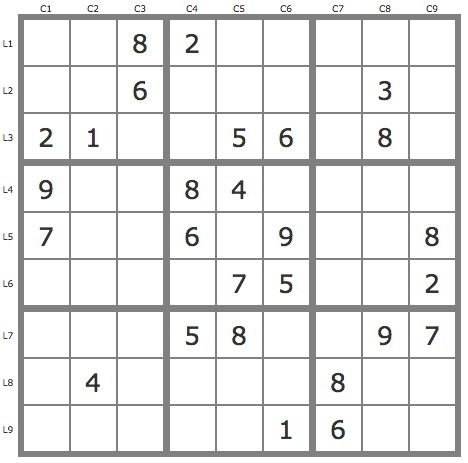
La grille -614Grille de niveau 14/15 conventionnel.
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 14/05/2019)
Bonjour 4 placements pour cette grille ne présentant pas curieusement la symétrie centrale de répartition des dévoilés par l'absence d'un dévoilé dans L7C2. Une taille 4 en première approche: P(3L1C6)) aisée à déceler couvre la grille. Étudions son antipiste P'. P'.P(3L4C6) est invalide. P'.P(2L4C6).P(1L5C5) est invalide. Enfin on vérifie les invalidités de P'.P(2L4C6).P(1L6C4).P(4K1C6 et P'.P(2L4C6).P(1L6C4).P(4L2C4) Je vais vérifier l'importance de la présence éventuelle de 3L7C2 assurant une symétrie centrale de répartitions des dévoilés, symétrie dont j'ignore toujours l'éventuelle importance. PS. Un petit bonjour à Paolo dont j'espére étudier bientôt les solutions sur ce forum.
De François C.
(Publié le 14/05/2019)
Bonsoir, P(3L4C6) invalide => suppr. candidat => applic. TB P(3L7C6) invalide => suppr. candidat => applic. TB P(3L3C4) invalide => suppr. candidat => applic. TB => solution Taille 3.
De Robert Mauriès
(Publié le 15/05/2019)
@ François C : Belle résolution François. J'étais aussi sur une voie analogue avec les 3 de C6 puisque le 3L1C6 est un backdoor, mais je n'ai pas réussi à montrer l'invalidité de P(3L8C6) directement qui aurait réduit à 3 la taille de la résolution. Bravo pour votre vista, car il fallait exploiter les 3 autrement comme vous l'avez fait !
De Claude Renault
(Publié le 15/05/2019)
4 placements par TB P(23)L7C6 invalide ; P(4L7C6)valide P(4L3C4) solution Pour l’unicité, P(379L3C4).P(4L3C7) et P(379L3C4).P(7L3C7) invalides
De Robert Mauriès
(Publié le 15/05/2019)
@ Claude Renault : Bonjour Claude. Vous annoncez que P(4L3C4) couvre la grille après avoir valider 4L7C6, mais il me semble que ce n'est pas le cas, sauf à utiliser la règle du rectangle interdit. Si tel est le cas vous ne pouvez plus aborder la question de l'unicité. Qu'en est-il ?
De Claude Renault
(Publié le 15/05/2019)
@ Robert Mauriès : bonjour Robert ; j'ai effectivement utilisé le rectangle interdit pour montrer que P(23L7C6) est invalide ; en fait, je suis parti du raisonnement selon lequel la double solution apportée par un RI n'est valable que lorsque la piste qui le génère est valide
De Claude Renault
(Publié le 15/05/2019)
@ Robert Mauriès : après reprise et sauf erreur, je trouve P(23L7C6) invalide sans passer par le RI (2 fois le 4 en C7)
De Robert Mauriès
(Publié le 15/05/2019)
@ Claude Renault : Effectivement P(23L7C6) est directement invalide. C'est P(4L3C4) qui selon moi ne couvre pas la grille sans utiliser un RI, c'est à dire n'est pas une solution directe, et pour laquelle je vous questionne.
De Claude Renault
(Publié le 15/05/2019)
@ Robert Mauriès : je n'ai pas le temps ce soir de regarder ce problème mais je me pose la question suivante : quand on tombe, comme dans le cas présent, sur un RI pour couvrir la grille, ne peut-on démontrer l'unicité de cette solution en démontrant que la piste devient invalide si on conserve le RI (en supprimant la partie qui l'empêche) ?
De Robert Mauriès
(Publié le 15/05/2019)
@ Claude Renault : Si la grille est à solutions multiples, la présence d'une formation en rectangle cachée (RI) ne peut pas être utilisée pour valider l'ensemble qui empêche le RI effectif. On peut trouver plein des contre-exemples. La présence d'un RI dans une piste valide est alors possible. En conséquence, l'utilisation d'un RI caché ne permet pas de statuer sur l'unicité. En revanche, un RI caché peut être utilisé pour construire une bifurcation d'une piste, une branche avec le RI effectif et une branche avec l'ensemble qui empêche le RI effectif (Voir ma résolution de la grille 607). Donc oui, utiliser comme cela le RI permet de démontrer l'unicité si la branche obtenue avec le RI effectif est invalide, mais vous ne l'avez pas fait dans votre résolution visant à prouver l'unicité sur la grille 614.
Ajouter un commentaire
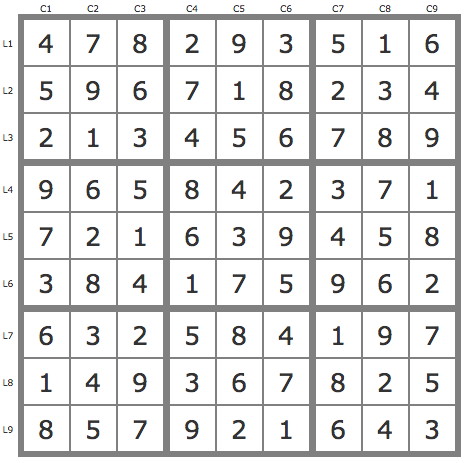
La solution
Les TB permettent 4 placements.
Voir en suite la résolution de taille 3 proposée sur le Forum.
 En savoir plus ...
En savoir plus ...




