S'identifier S'inscrire
assistant-sudoku.com
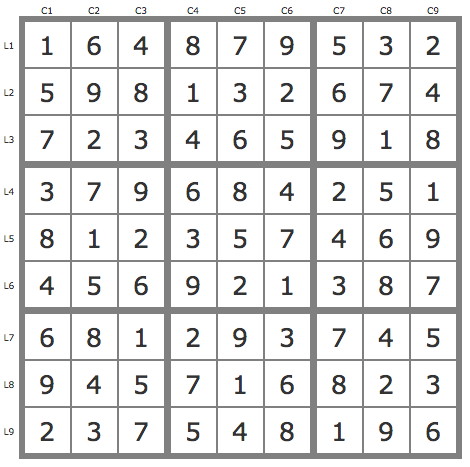
Grille Sudoku résolue
La grille -607Grille de niveau 15 conventionnel.
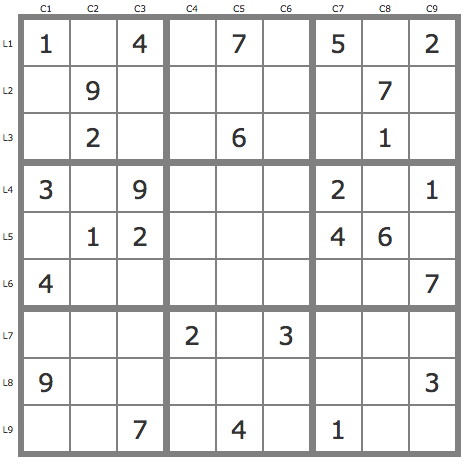
Commentaires sur cette grille
De Paolo
(Publié le 20/04/2019)
Bonsoir, 11 placements par les TB initiales. P(5L7C9)=>couvre la grille 1)P(8L7C9) => contradiction 2)P(9L7C9) => contradiction =>solution. ou 1)P(8L6C2) => contradiction Solution par le croisement de deux pistes conjuguées 5L4C8 et 8L4C8
De Robert Mauriès
(Publié le 21/04/2019)
Bonnes Pâques à tous ! Je vous invite à voir la résolution détaillée de cette grille proposée dans "Résolutions guidées" qui utilise un Rectangle caché pour réaliser une extension.
Ajouter un commentaire
La solution
La résolution proposée ci-dessous n'est pas la plus rapide (voir le forum). Son but est de montrer comment manipuler une extension en se servant d'un RI caché.
Après réduction de la grille par les TB (11 placements), le jeu de pistes le plus évident est celui issu de la paire 5B4 ( ou équivalentes 58L5C1 ou L6C2, etc..), pistes que l'on trace partiellement comme sur la figure ci-dessous et qui permettent quelques éliminations (candidats barrés en rouge) par interactions des deux pistes.
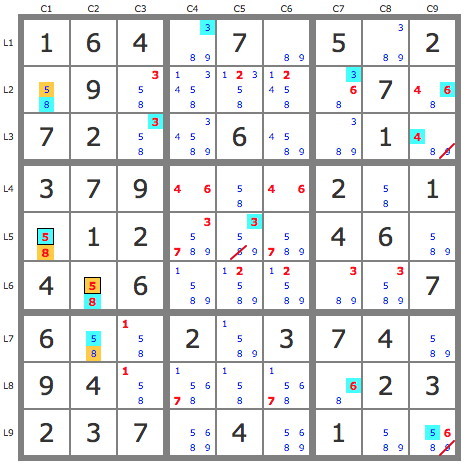 La piste bleue se développe bien, et même jusqu'à contradiction si on poursuit... mais pour exploiter les interactions des deux pistes, on préfère développer la piste jaune par une extension.
On se sert ici du Rectangle caché 15L78-C35 de la piste jaune pour construire cette extension, en vérifiant que la P-antipiste verte P(5L6C2).P'(E) où E={9L7C5, 8L8C5} est invalide (ce qui est fort probable si la grille est à solution unique) et se confirme par une impossibilité dans la case L5C9.
Ainsi (voir définition 8-3 de Théorie des pistes), P(5L6C2).P(E) est une extension de la piste jaune P(5L6C2).
La piste bleue se développe bien, et même jusqu'à contradiction si on poursuit... mais pour exploiter les interactions des deux pistes, on préfère développer la piste jaune par une extension.
On se sert ici du Rectangle caché 15L78-C35 de la piste jaune pour construire cette extension, en vérifiant que la P-antipiste verte P(5L6C2).P'(E) où E={9L7C5, 8L8C5} est invalide (ce qui est fort probable si la grille est à solution unique) et se confirme par une impossibilité dans la case L5C9.
Ainsi (voir définition 8-3 de Théorie des pistes), P(5L6C2).P(E) est une extension de la piste jaune P(5L6C2).
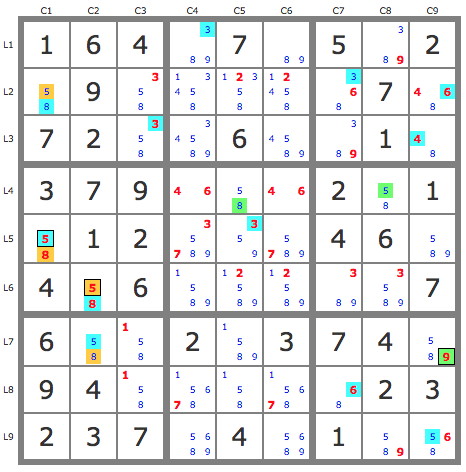 La construction de P(5L6C2).P(E) se fait en recherchant le croisement de ces deux branches verte P(5L6C2).P(9L7C5) et violette P(5L6C2).P(8L8C5). Le 3L2C5 en fait partie qui est donc un candidat de l'extension.
La construction de P(5L6C2).P(E) se fait en recherchant le croisement de ces deux branches verte P(5L6C2).P(9L7C5) et violette P(5L6C2).P(8L8C5). Le 3L2C5 en fait partie qui est donc un candidat de l'extension.
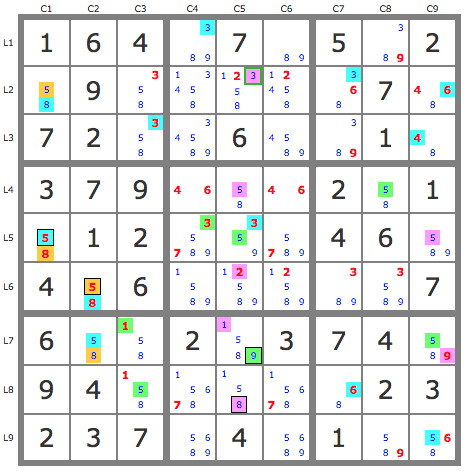 Dès lors l'extension (en jaune) de la piste jaune se développe largement par les TB et croise la piste bleue sur le 3L3C3 qui est donc solution, et plusieurs éliminations sont faites par interaction (candidats barrés en rouge) ...
Dès lors l'extension (en jaune) de la piste jaune se développe largement par les TB et croise la piste bleue sur le 3L3C3 qui est donc solution, et plusieurs éliminations sont faites par interaction (candidats barrés en rouge) ...
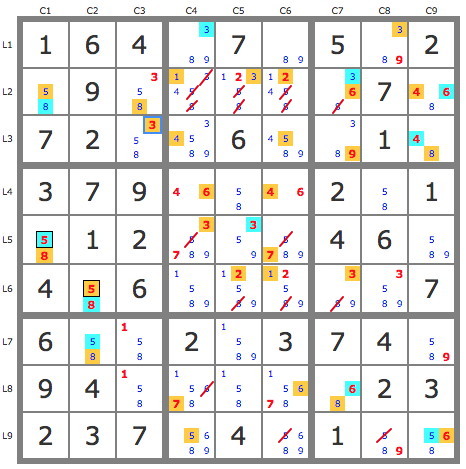 Mais la piste jaune se développe jusqu'à couvrir la grille tandis que la piste bleue peut être développée par les TB jusqu'à rencontrer une impossibilité, toutes choses faciles à vérifier et laissées à votre initiatives.
Remarques : on pouvait aussi résoudre par jeux de pistes successifs, (après avoir dès le début invalidé la piste bleue et placer les candidats de la piste jaunes) en choisissant comme second jeu de pistes celui formé de P(E) et P'(E).
Mais la piste jaune se développe jusqu'à couvrir la grille tandis que la piste bleue peut être développée par les TB jusqu'à rencontrer une impossibilité, toutes choses faciles à vérifier et laissées à votre initiatives.
Remarques : on pouvait aussi résoudre par jeux de pistes successifs, (après avoir dès le début invalidé la piste bleue et placer les candidats de la piste jaunes) en choisissant comme second jeu de pistes celui formé de P(E) et P'(E).
 En savoir plus ...
En savoir plus ...




