S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -591Grille de niveau 14/15 conventionnel.
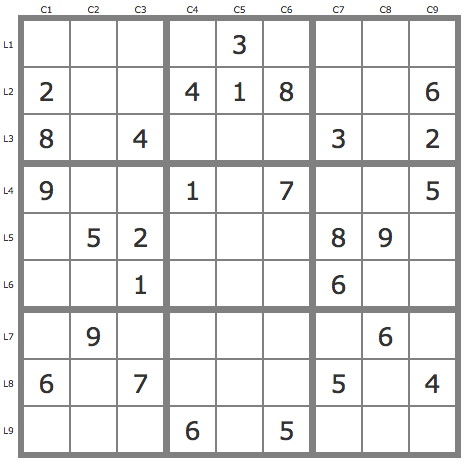
Commentaires sur cette grille
De Robert Mauriès
(Publié le 02/03/2019)
Réduction de la grille par les TB (5 placements) puis utilisation de la TDP. Voici une résolution de taille 4. - P(3L6C9) invalide -> placement de 7L6C9. - P(5L1C1).P(38L7C9) invalide -> placement des 19 candidats de P(1L1C1). Puis : - P(7L7C7) couvre la grille alors que P(7L9C8) est invalide. On peut reprendre différemment cette résolution comme suit : - P(5L2C3) couvre la grille (backdoor). - P(5L1C3) invalide. - P(5L1C1).P(37L6C9).P(38L7C9) invalide.
De Francis Labetoulle
(Publié le 02/03/2019)
Bonjour Un autre taille 4 (en attendant mieux?) à partir de la cellule pivot L2C3: P(3L2C3) donne 2 invalidités avec les deux 3 restants de L4. P(5L2C3) couvre la grille. P(9L2C3) donne de même 2 invalidités avec les deux 3 restants de L4.
De Paolo
(Publié le 02/03/2019)
Bonjour, 5 placements par les TB initiales. P(5L2C3) => couvre la grille 1)P’(3L4C8) => contradiction=>validation P(3L4C8)+2 placements 2)P(3L2C3) => contradiction 3)P(9L2C3) => contradiction =>solution ou 1)P’(3L4C8) => contradiction=>validation P(3L4C8)+2 placements 2P(1L3C2) => contradiction 3)P(6L3C2)=> contradiction =>validation P(7L3C2) =>solution. ou P(8L9C8) => couvre la grille 1)P’(3L4C8) => contradiction=>validation P(3L4C8)+2 placements 2)P(8L8C8) => contradiction 3)P(8L1C8) => contradiction =>solution
De Robert Mauriès
(Publié le 02/03/2019)
@ Paolo : Bien vu Paolo ce passage clé de la résolution par l'antipiste issue du 3L4C8, ou ce qui revient au même de la piste issue de l'ensemble 24L4C8. Cela permet de réduire à 3 la taille de résolution et donc le niveau TDP de la grille. Bravo !
De Paolo
(Publié le 02/03/2019)
Bonjour, 5 placements par les TB initiales. P(7L2C8) => couvre la grille 1)P(5L2C8).P’(3L6C1) => contradiction 2)P(5L2C8).P(3L6C1).P(7L2C7) => contradiction 3)P(5L2C8).P(3L6C1).P(9L2C7) => contradiction =>solution
De Claude Renault
(Publié le 02/03/2019)
TB : 5 JP (3,5,9L2C3) ; le 5 couvre le grille 3L2C3.6L1C2 invalide ; 3L2C3.1L1C2.4L4C2 invalide ; 9L2C3.6L3C2 invalide ; 9L2C3.7L3C2 invalide.
De Francis Labetoulle
(Publié le 02/03/2019)
Voici un taille 3, utilisant préalablement une partition de la case L6C8. P(37L6C8) est invalide. Son antipiste P' donne avec les candidats de la case pivot L2C3: P'.P(3L2C3) invalide, P'.P(9L2C3) invalide et P'.P(5L2C3) solution.
De François C.
(Publié le 02/03/2019)
Bonsoir, Les TB donnent 5 placements et quelques suppressions. Ensuite: P(348L9C2) => contradiction P(12L9C2).P(7L2C7) => contradiction P(12L9C2).P(9L2C7) => solution Résolution de taille 2 (j’en ai trouvé seulement deux).
De Paolo
(Publié le 03/03/2019)
@ François C: Bonsoir, La deuxième résolution que vous avez trouvée est la suivante, qui utilise la même première contradiction, ou est-ce une autre complètement différente? 5 placements par les TB initiales. 1)P(438L9C2) => contradiction 2)P(12L9C2).(56L1C3) => contradiction 3)P(12L9C2).(9L1C3) =>solution
De Robert Mauriès
(Publié le 03/03/2019)
@ Paolo et François : Bravo à François pour cette résolution de taille 2 à base d'ensembles, un modèle de résolution ! Votre dernière résolution Paolo est différente de celle de François dans le choix des ensembles générateurs des extensions de P(12L9C2), mais elle est équivalente à celle de François car les pistes de JP(569L1C3) et de JP(79L2C7) sont identiques deux à deux : P(56L1C3)=P(7L2C7) et P(9L1C3)=P(9L2C7). Dit autrement les ensembles générateurs des extensions de vos résolutions sont liés fortement J'en profite pour rappeler la définition de deux jeux de pistes équivalents : deux jeux de pistes sont équivalents lorsque leurs pistes sont identiques deux à deux. Cela généralise la notion classique de lien fort. Dès lors, on considère que deux résolutions sont différentes lorsqu'elles utilisent des jeux de pistes qui ne sont pas tous équivalents. Dans le cas contraire elles sont équivalentes.
De François C.
(Publié le 03/03/2019)
@ Paolo : Bonjour, j’ai été un peu vite en disant que j’ai trouvé 2 résolutions différentes. Je voulais dire en fait que j’ai trouvé 2 unités de départ possibles conduisant à une taille 2. La première est L9C2 et il se trouve que toutes les extensions efficaces de la piste valide sont équivalentes (voir remarque de Robert). La deuxième est 3B7 mais là aussi, en y regardant de plus près, on obtient des pistes quasi identiques à celles du premier cas.
De Paolo
(Publié le 03/03/2019)
@ Robert Mauriès: Bonjour, Ce que vous dites au sujet de l’équivalence des solutions “deux jeux de pistes sont équivalents lorsque leurs pistes sont identiques deux à deux” ce n'est pas tout à fait clair pour moi car pendant que il est évident que deux pistes qui sont de backdoors sont identiques, deux pistes invalides peuvent se développer pour atteindre la contradiction d'une manière différente (dépend de l'ordre dans lequel les TB sont appliqués) sans qu'il soit nécessaire que tous les deux éléments qui génèrent les deux pistes soient présents dans l'ensemble généré. En pratique, la question que je pose est la suivante lorsque deux pistes invalides sont identiques?
De Robert Mauriès
(Publié le 03/03/2019)
@ Paolo : En effet Paolo, il convient d'être plus précis sur cette définition d'équivalence. Quand je dis que deux pistes sont identiques, je veux dire que leurs traces sont identiques, la trace d'une piste étant l'ensemble des candidats de la piste que l'on arrive à construire avec les seules TB. Donc, la bonne définition est : deux pistes sont équivalentes lorsque leurs traces sont identiques. Cette définition s'applique aux pistes quelque soit leur nature, valide ou invalide. On peut énoncer le théorème suivant qui permet de dire si deux pistes sont équivalentes : Si P(E1) contient E2 et P(E2) contient E1, P(E1) et P(E2) sont équivalentes.
Ajouter un commentaire
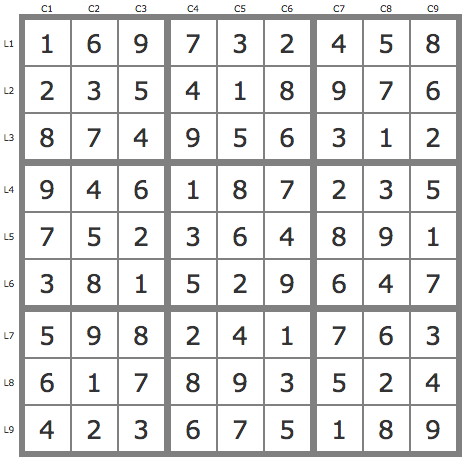
La solution
Réduction de la grille par les TB (5 placements) puis utilisation de la TDP. Voici une résolution de taille 4.
- P(3L6C9) invalide -> placement de 7L6C9.
- P(5L1C1).P(38L7C9) invalide -> placement des 19 candidats de P(1L1C1).
Puis :
- P(7L7C7) couvre la grille alors que P(7L9C8) est invalide.
On peut reprendre différemment cette résolution comme suit :
- P(5L2C3) couvre la grille (backdoor).
- P(5L1C3) invalide.
- P(5L1C1).P(37L6C9).P(38L7C9) invalide.
Voir aussi les résolutions de taille 2 proposées par François et Paolo dans le forum, un modèle de résolution à base d'ensembles.
 En savoir plus ...
En savoir plus ...




