S'identifier S'inscrire
assistant-sudoku.com
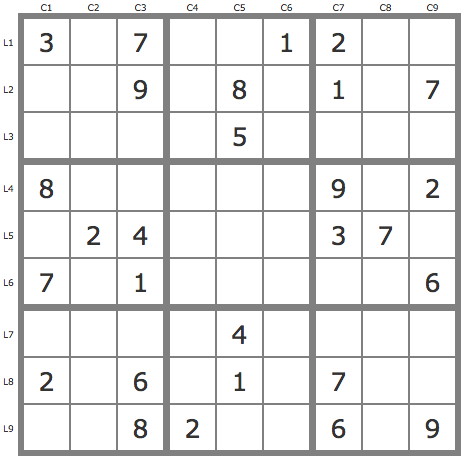
Grille Sudoku résolue
La grille -589Grille de niveau 4 TDP.
Commentaires sur cette grille
De Robert Mauriès
(Publié le 23/02/2019)
Réduction de la grille par les TB (4 placements) puis exploitation du bloc B4 pour une résolution de taille 5. - P(3L4C3) invalide -> 2 placements. - P(6L5C1).P(4L3C7) solution. - P(6L5C1).P(8L3C7).P(49L1C4) invalide. - P(6L4C2).P(15L7C1) invalide. Mais sans doute peut-on faire mieux en matière de taille de résolution
De Paolo
(Publié le 23/02/2019)
Bonjour, 4 placements par les TB initiales. P(8L3C7).P(4L3C9)=> contradiction P(8L3C7).P(3L3C9)=> contradiction=>validation P(4L3C7),(2 placements) P(8L3C9)=> contradiction=>validation P(3L3C9),(3 placements) P(9L1C5)=> contradiction=>validation P(6L1C5)=>solution.
De Paolo
(Publié le 23/02/2019)
Bonjour, Une autre solution de taille 4 4 placements par les TB initiales. P(9L3C8).P(8L3C9)=> contradiction P(9L3C8).P(8L3C7)=> contradiction P(9L3C8).P(8L3C2)=> contradiction=>validation P(9L1C8), (11 placements) P(5L7C7)=> contradiction=>validation P(8L7C7)=>solution.
De François C.
(Publié le 24/02/2019)
Bonjour, Les TB donnent 4 placements puis une paire. Ensuite, voici une autre résolution de taille 4 en partant des 4 de la ligne 6 et en prenant comme extensions la case L1C4 et les 3 du bloc 4 : P(4L6C47).P(4L1C4) => contradiction P(4L6C47).P(69L1C4) => contradiction P(4L6C68).P(3L4C2) => solution P(4L6C68).P(3L4C3) => contradiction P(4L6C68).P(3L6C2) => contradiction
De Claude Renault
(Publié le 24/02/2019)
TB : 4 P(5L5C1) invalide P(6L5C1).P(8L7C7).P(4L2C2) couvre la grille ; P(6L5C1).P(8L7C7).P(6L2C2) invalide P(6L5C1).P5L7C7) invalide
De Robert Mauriès
(Publié le 24/02/2019)
@ Claude Renault : Bonjour Claude. Que faites-vous du 9L5C1 ?
De Claude Renault
(Publié le 25/02/2019)
@ Robert Mauriès : un oubli (je suis en train de mettre au point l'adaptation de mon langage de résolution avec mon modèle de grille et le langage TDP ; ce n'est pas tout à fait au point)
Ajouter un commentaire
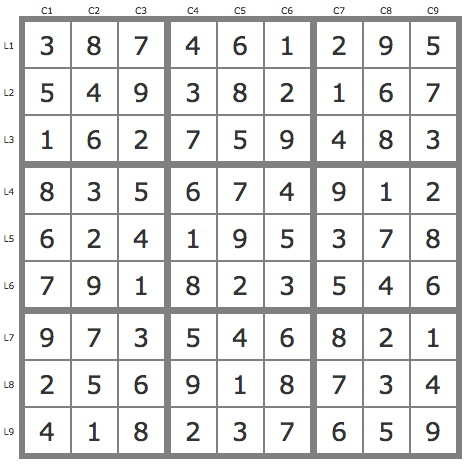
La solution
Réduction de la grille par les TB (4 placements) puis exploitation du bloc B4 pour une résolution de taille 5.
- P(3L4C3) invalide -> 2 placements.
- P(6L5C1).P(4L3C7) solution.
- P(6L5C1).P(8L3C7).P(49L1C4) invalide.
- P(6L4C2).P(15L7C1) invalide.
Voir aussi le forum où deux résolutions de taille 4 sont proposées, dont l'une utilise la notion de paires d'ensembles.
 En savoir plus ...
En savoir plus ...




