S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -584Grille de niveau 15 conventionnel.
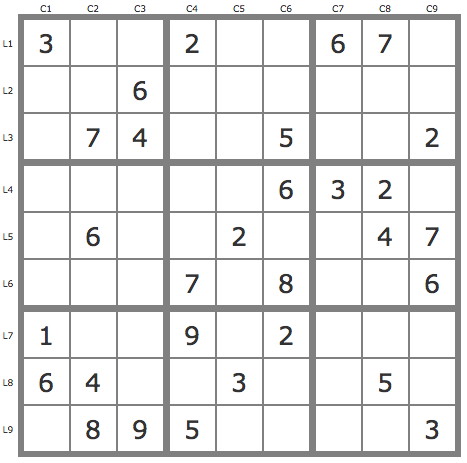
Commentaires sur cette grille
De Paolo
(Publié le 11/02/2019)
Bonsoir, 2 placements par les TB initiales. P(5L5C3)=>couvre la grille 1)P(8L5C3) => contradiction 2)P(1L5C3).P(2L9C1) => contradiction 3)P(1L5C3).P(7L9C1) => contradiction=>solution.
De Robert Mauriès
(Publié le 12/02/2019)
@ Paolo : Belle résolution Paolo, bravo !
De François C.
(Publié le 12/02/2019)
Bonjour, 2 placements avec les TB, et ensuite: P(1L5C4).P(5L5C3) => solution P(1L5C4).P(8L5C3) => contradiction P(3L5C4).P(6L7C8) => contradiction P(3L5C4).P(8L7C8) => contradiction
De Robert Mauriès
(Publié le 12/02/2019)
@ François C : Bonjour François. Résolution de taille 3 intéressante car elle n'utilise pas les backdoors de la grille. Bien vu !
De François C.
(Publié le 12/02/2019)
@ Robert Mauriès : Vous voulez dire que je n'utilise pas de backdoor dans la paire initiale (13L5C4). J'ajoute que cette paire ne contient pas non plus d'anti-backdoor (ce que je définis comme un candidat qui mène directement à une contradiction avec les seules TB). En fait, en faisant tourner ma moulinette informatique, j'ai observé ceci: il y a 18 paires de candidats indépendantes. Parmi celles-ci seulement 4 paires contiennent un anti-backdoor et aucune ne contient un backdoor. De plus, il n'y a que deux paires qui constituent un bon démarrage pour une résolution de taille 3: 13L5C4 (que j'ai donnée) et 68L7C8. Et bien aucune des deux ne contient un backdoor ou un anti-backdoor ! Cela n'est effectivement pas très prévisible. Par ailleurs il y a beaucoup de résolutions de taille 3 utilisant des paires d'ensembles et quelques-unes utilisant des triplets (comme celle de Paolo).
De Robert Mauriès
(Publié le 13/02/2019)
@ François C : Bonjour François. Ce que je voulais dire en qualifiant votre résolution d'intéressante, c'est qu'elle ne s'appuie pas sur un backdoor ou un anti-backdoor à priori difficiles à déceler "à la main", mais sur la construction plus rationnelle d'un jeu de pistes que l'on prolonge ensuite par des extensions. Merci pour votre analyse globale de la grille fournie par votre lociciel. Ceci dit, cette grille compte plusieurs backdoors (7L9C5, 5L5C3, 8L3C7, 9L5C7, etc...) et il est naturel dès lors qu'ils sont identifiés de chercher à les utiliser puis de prouver l'unicité en montrant que les antipistes correspondantes sont invalides, ce qu'a fait Paolo avec succès. Voici d'ailleurs une résolution originale qui utilise deux backdoors engendrant un jeu de pistes conjuguées : - P(5L5C3) et P(9L5C7) couvrent la grilles respectivement, car 5L5C3 et 9L5C7 sont des backdoors. - L'antipiste P'({5L5C3,9L5C7}) est invalide car P'.P(9L5C1) et P'.P(9L5C6).P(68L7C8) sont invalides. - En conséquence P(5L5C3) et P(9L5C7) sont conjuguées et leur intersection couvre la grille en fournissant une solution unique.
De François C.
(Publié le 13/02/2019)
@ Robert Mauriès : Bonjour, Tout à fait d’accord , mais ma remarque se limitait à des paires de candidats appartenant à une même entité. En effet mon logiciel ne prend en compte que les paires, triplets, n-uplets (n>3) de candidats ou d’ensembles de candidats appartenant à une même entité, ce qui n’est déjà pas mal. Effectivement cela ne représente qu’une partie des possibilités, car on peut construire des ensembles à partir de candidats quelconques et là, bien évidemment, le nombre de combinaisons devient gigantesque et il serait impossible de les tester dans un temps raisonnable.
De Paolo
(Publié le 13/02/2019)
Bonsoir, Une résolution similaire à celle décrite par François à partir de la paire de 6 du B8 (sans backdoor ni anti-backdoor dans le couple initial ). 2 placements par les TB initiales. P(6L7C5).P(1L9C7)=>solution P(6L7C5).P(2L9C7)=> contradiction P(6L9C5).P(4L1C6)=> contradiction P(6L9C5).P(9L1C6)=> contradiction Également dans ce cas, nous utilisons une backdoor initiale P (1L9C7) apparemment masquée semblable à P (5L5C3) dans le cas de François.
De François C.
(Publié le 15/02/2019)
@ Paolo : Bonjour, Effectivement 6B8 est une paire équivalente à 68L7C8, qui est la seule avec 13L5C4 que j’ai trouvée pour démarrer une résolution de taille 3.
Ajouter un commentaire
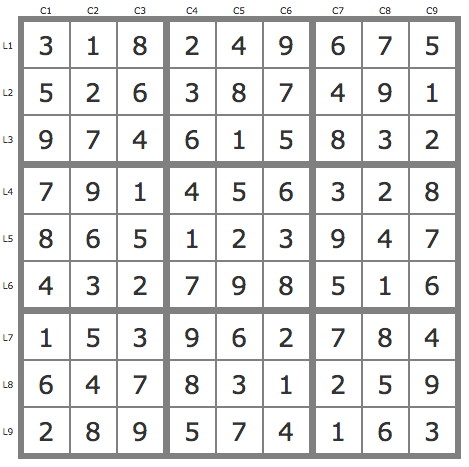
La solution
Après réduction de la grille par les TB (2 placements), une résolution originale utilise deux backdoors engendrant un jeu de pistes conjuguées. En effet :
- P(5L5C3) et P(9L5C7) couvrent la grilles respectivement, car 5L5C3 et 9L5C7 sont des backdoors.
- L'antipiste P'({5L5C3,9L5C7}) est invalide car P'.P(9L5C1) et P'.P(9L5C6).P(68L7C8) sont invalides.
- En conséquence P(5L5C3) et P(9L5C7) sont conjuguées et leur intersection couvre la grille en fournissant une solution unique.
Voir aussi les solutions proposées dans le forum.
 En savoir plus ...
En savoir plus ...




