S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -577Grille de niveau 12 conventionnel.
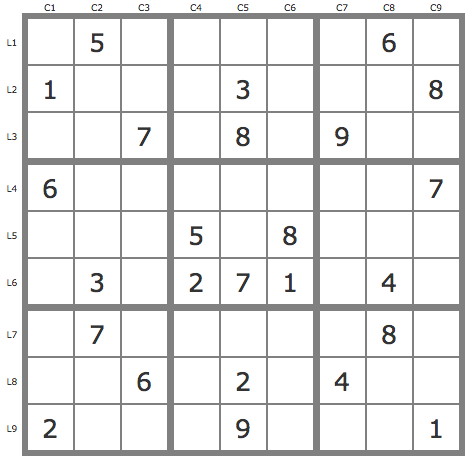
Commentaires sur cette grille
De Robert Mauriès
(Publié le 24/01/2019)
Résolution de taille 4 en attendant de trouver mieux. Après le 6 placements que permettent les TB, on porte son attention sur la case L3C9, en remarquant que P(2L3C9) et P(5L7C9) se développant facilement sont invalides. Dès lors cela permet par les TB de placer 4 candidats supplémentaires. On tire ensuite la solution de la case L6C9 avec P(9L3C9) qui couvre la grille, P(5L6C9) et P(6L6C9) étant invalides.
De Paolo
(Publié le 25/01/2019)
Bonjour, 6 placements par les TB initiales. P(9L7C1) => couvre la grille 1)P(4L7C1).P(4L5C2) => contradiction 2)P(4L7C1).P(9L5C2) => contradiction 3)P(3L7C1) => contradiction =>solution. ou P(4L9C2) => couvre la grille 1)P(8L9C2).P(4L5C2) => contradiction 2)P(8L9C2).P(9L5C2) =>contradiction=>solution. ou P(1L7C3) => couvre la grille 1)P'(1L7C3).P(9L5C2) => contradiction 2)P'(1L7C3).P'(9L5C2) =>contradiction=>solution.
De Robert Mauriès
(Publié le 26/01/2019)
@ Paolo : Belles résolutions de taille 2 Paolo, ce qui établit à 2 le niveau TDP de cette grille.
De Claude Renault
(Publié le 27/01/2019)
@ Paolo : dans votre 2ème résolution, je trouve bien comme vous les invalidités du 8L9C2 mais je n'arrive pas à montrer que le 4 couvre la grille (mes seules résolutions sont : 4B4 ; 1,4 et 8 de B7 ; 1,8 de B8)
De Paolo
(Publié le 27/01/2019)
@ Claude Renault : Bonsoir, Un ordre d'insertion logique possible peut être le suivant: 4L9C2=>4L5C3;6L3C4;6L2C2;2L3C2;2L4C3;1L7C3(backdoor initiale) ;1L8C4;8L9C4(backdoor initiale);9L2C3;5L3C6;5L6C1….
Ajouter un commentaire
La solution
Après le 6 placements que permettent les TB, on porte son attention sur la case L3C9, en remarquant que P(2L3C9) et P(5L7C9) se développant facilement sont invalides. Dès lors cela permet par les TB de placer 4 candidats supplémentaires.
On tire ensuite la solution de la case L6C9 avec P(9L3C9) qui couvre la grille, P(5L6C9) et P(6L6C9) étant invalides.
Il existent des résolutions plus rapides proposées par Paolo dans le forum à partir des cases L7C3 ou L9C2 qui comptent des backdoors.
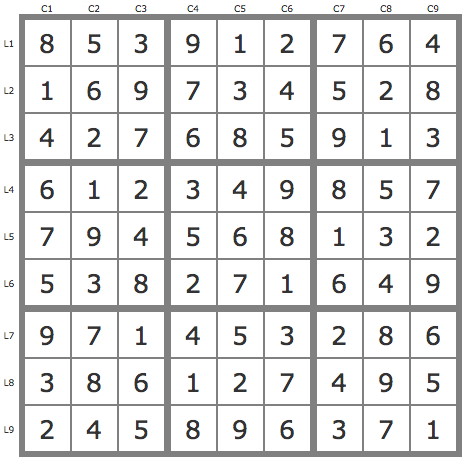
 En savoir plus ...
En savoir plus ...




