S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -560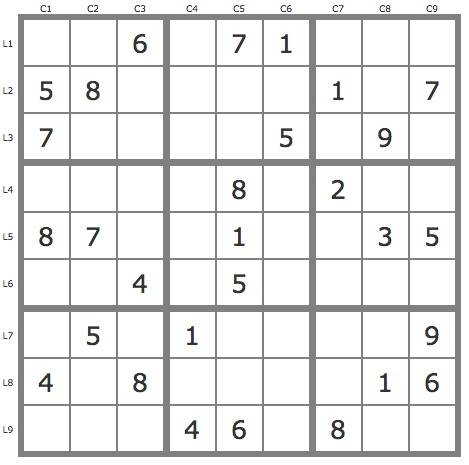
Commentaires sur cette grille
De Francis Labetoulle
(Publié le 28/11/2018)
Bonsoir La première grille peut se résoudre en partant de L5C9 ( solution avec le 9...) Seconde grille: P(4 L3C5) est invalide donc validation de 4L2C5. Puis, avec la case L7C5: P(2L7C5) couvre la grille tandis que P(3 L7C5) donne deux invalidités avec les 2 de L2.
De François C.
(Publié le 29/11/2018)
Bonjour, Les TB donnent 6 placements puis 2 alignements. Ensuite, dans la case L3C5 : le 3 est un backdoor, P(4) conduit directement à une contradiction et P(2).P(26L2C8) est invalide.
De Paolo
(Publié le 29/11/2018)
Bonsoir, 1)6 placements par les TB initiales. 2) P(3L7C7)=> solution 3) P(7L7C7) => contradiction 4) P(4L7C7).P(3L8C7) => contradiction 5) P(4L7C7).P(7L8C7) => contradiction
De Paolo
(Publié le 29/11/2018)
@ Robert Mauriès et François Cordoliani: Bonsoir, La solution proposée par Cordoliani a suscité des doutes quant à la nomenclature des extensions. En fait, dans la résolution de François je pense que P(2L3C5).P(26L2C8) peut avoir deux interprétations, la première (correcte) pour indiquer synthétiquement les deux contradictions de P(2L3C5).P(2L2C8) et P (2L3C5).P(6L2C8), le deuxième que la piste P(2L3C5).P(26L2C8) mène directement à une contradiction (incorrecte) car l'ensemble des candidats 2 et 6 dans la case L2C8 est une entité de G et par conséquent le P (2L3C5).P(26L2C8) étant identique à P(2L3C5) ne conduit pas, avec la seule utilisation de TB à contradiction.
De François C.
(Publié le 30/11/2018)
@ Paolo : Bonjour, Vous soulevez un problème de notation qui n’est peut-être pas très correcte sachant qu’il faut faire la distinction entre une piste et sa trace (voir théorie des pistes). J’ai utilisé la notation P(A).P(E) où E est une entité (ici cachée) par souci de concision, mais en réalité j’ai bien développé les 2 branches P(2L5C3).P(2L2C8) et P(2L5C3).P(6L2C8) pour aboutir à deux invalidités. C’était aussi pour indiquer qu’il y a sûrement moyen d’utiliser les propriétés de recouvrement des 2 branches, sans les développer toutes les deux jusqu’à la contradiction.
De Robert Mauriès
(Publié le 01/12/2018)
@ Paolo et F. Cordoliani : Bonjour. Vous avez tous les deux raisons car d'une manière générale on a : P1.P(E) invalide <=> P1.P(Ak) invalide pour tout Ak de E. En revanche, s'agissant de la taille de la solution, il convient de distinguer le cas où P1.P(E) est montrée invalide directement (donc sans construire les branches séparemment) de celui où l'invalidité est soit démontrée branche par branche soit après avoir construit P(E) par croisement des branches. Dans le premier cas l'invalidité compte pour 1, dans les deux autres cas elle est égale au nombre de branches mises en jeu.
Ajouter un commentaire
La solution
 En savoir plus ...
En savoir plus ...




