S'identifier S'inscrire

assistant-sudoku.com

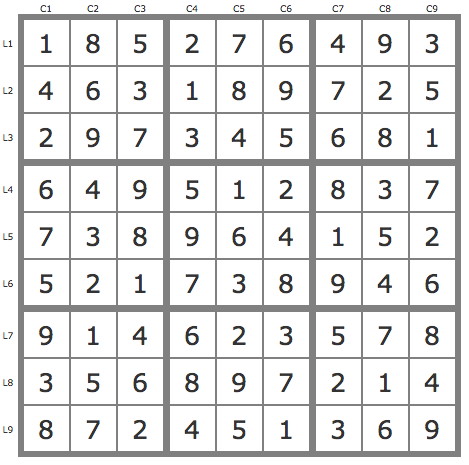
Grille Sudoku résolue

La grille -558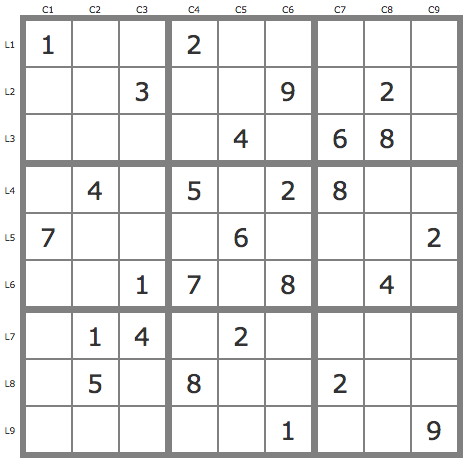

Afficher les commentaires Cacher les commentaires

Commentaires sur cette grille

De Paolo
(Publié le 17/11/2018)

Bonjour, 1)3 placements par les TB initiales. 2)P(4L5C6).P(3L3C4)=> solution 3)P(3L5C6).P(3L7C1) => contradiction 4)P(3L5C6).P(6L7C1) => contradiction 5)P(4L5C6).P(1L3C4).=> contradiction

De Claude Renault
(Publié le 17/11/2018)

TB : 3 résolution à partir de 3 ensembles invalides L9C3 : 67 invalide résout le 2 L4C5 : 39 invalide résout le 1 L9C4 : 36 invalide résout le 4 et couvre la grille

De St
(Publié le 18/11/2018)

Bonjour La solution donnée est fausse : il n'y a pas de 6 en C8 ! Crdlt

De Robert Mauriès
(Publié le 18/11/2018)

@ Stéphane D. : Effectivement, merci de me l'avoir signalé. La bonne solution a été mise en place.

De Francis Labetoulle
(Publié le 19/11/2018)

Bonjour J'essaie de satisfaire le cahier des charges en utilisant des pistes opposées dans un premier temps. L5 est pleine de promesses donc partons de P1 = (4L5C4) et P2 = (4L5C6). Soient Qa = (3L9C4) et Qb = (6L9C4) toutes deux opposées à P2. Les pistes (Qa+P1) et (Qb+P1) se révèlent toutes deux invalides, ce qui valide les candidats de P2. J'ose ensuite le *-wing des 1 de L7 (ici skyscraper pour les puristes) validant 1L4C5, et faisant apparaître deux réseaux "génériques" sur C4 dont les pistes associées se croisent pour couvrir la grille.

De Paolo
(Publié le 19/11/2018)

Bonjour, Une autre résolution: 1)3 placements par les TB initiales. 2)P(1L3C4).P(3L1C5)=>contradiction 3)P(1L3C4).P’(3L1C5)=>contradiction=>validation P(3L3C4) 4)P’(3L1C9)=>contradiction=>solution. La validation de la piste P(3L3C4) déclenche 22 backdoors. De nombreux antipistes de ceux-ci mènent à la solution.

De Frandou
(Publié le 21/11/2018)

@ Robert Mauriès : Bonjour, Concernant la solution que vous proposez je ne trouve pas le raisonnement qui fait passer la piste verte 1L5C4 par le 1 L2C7 . Je la vois passer par le 1L2C5 car il devient unique dans C5 et 1L3C9 car il est unique lui aussi dans L3 et comme il n’y a plus de 1 vert dans C7 la piste verte est bien invalide et donc ce qui valide bien le 1L4C5.

De Robert Mauriès
(Publié le 24/11/2018)

@ Frandou : Bonjour. La construction d'une piste peut se faire de plusieurs manières, en fonction des enchaînements que l'on suit. La votre est exacte. La mienne aussi car, partant du 1L5C4 je constate que C7 ne contient plus que le 1L2C7 qui est donc un candidat de la piste. Nos deux constructions conduisent au constat que cette piste est invalide et c'est pour cela qu'elles peuvent contenir deux candidats de la même ligne : le 1L2C5 et le 1L2C7. Rien d'anormal à cela, une piste invalide peut passer par tous les candidats de la grille (voir Théorie des pistes).

Ajouter un commentaire

La solution

Après simplification de la grille par les TB, on choisit le jeu de pistes issues de la paire 5B4 dont chaque piste contient quelques candidats. Les deux pistes se croisent sur le 6L6C9 que l'on place (solution), ce qui fait apparaître l'alignement 5L123C9 qui élimine les autres 5 de B3. 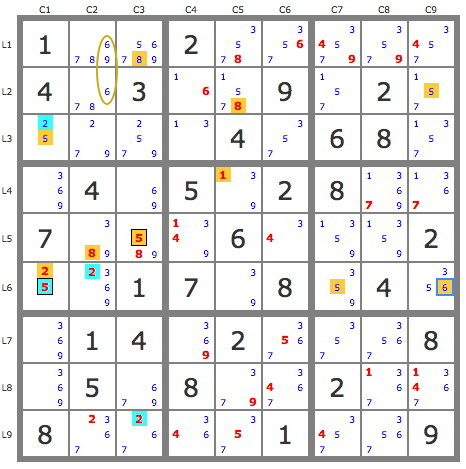Remarquons par ailleurs que la piste verte P(1L5C4), opposée à la piste jaune, est invalide (aucun 1 vert possible dans B2), ce qui valide le 1L4C5. Cette opération d'élimination est équivalente à un X-wing sur les 1. 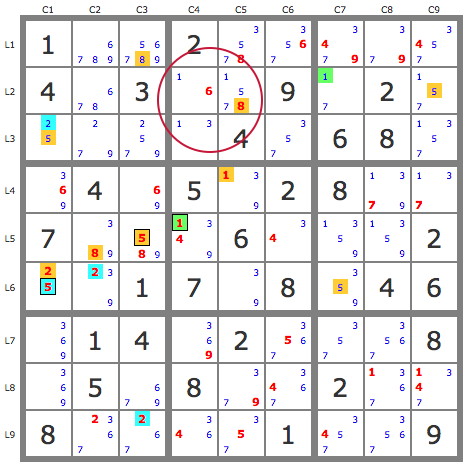La piste issue du 1L2C7 se développe largement pour constater qu'elle est opposée à la piste bleue dans L9C3, ce qui permet de dire qu'elle est invalide dans L5C7. Donc on peut valider le 7L2C7 comme solution de la case, et avec lui deux autres candidats de la grille. 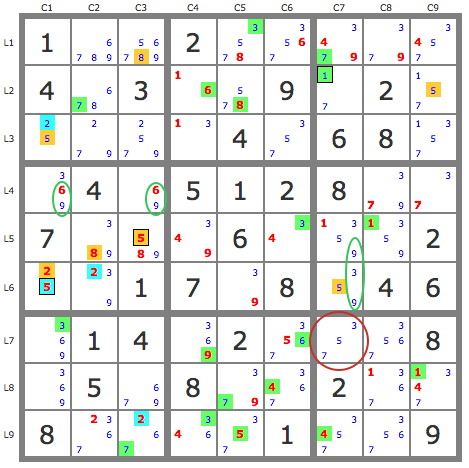Dès lors la piste jaune se développe pour aboutir à une contradiction dans L7C4, ce qui valide tous les candidats de la piste bleue. 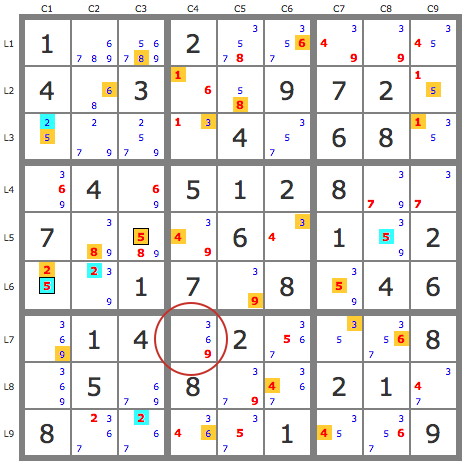La grille se termine alors avec un second jeu de pistes issue de la paire 3B4, P(3L4C1) est invalide et P(3L5C2) couvre la grille.