S'identifier           S'inscrire

assistant-sudoku.com

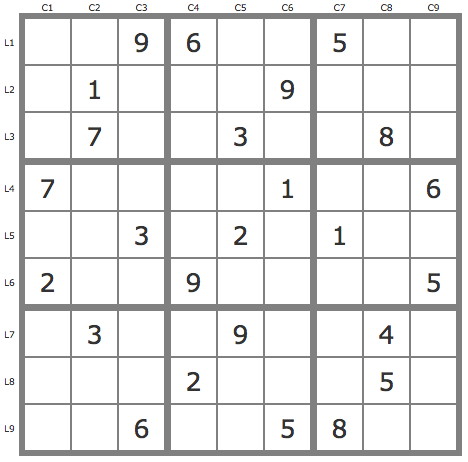
Grille Sudoku résolue

La grille -548
Grille de niveau 3 TDP.



Afficher les commentaires


Commentaires sur cette grille

De Robert Mauriès
(Publié le 06/10/2018)

Se reporter à "Voir la résolution" par le lien ci-dessus.

De Paolo
(Publié le 06/10/2018)

Bonjour, 4 placements par les TB initiales. P(6L6C5) => couvre la grille 1)P(6L8C5). P(7L5C8)=>contradiction 2)P(6L8C5). P(9L5C8).P(3L4C4)=>contradiction 3)P(6L8C5). P(9L5C8).P(3L9C4)=>contradiction=>validation P(6L6C5)=>soluton.

De François C.
(Publié le 07/10/2018)

Bonjour, Les TB donnent 4 placements et quelques suppressions avec 2 alignements. Ensuite j'utilise les cases L3C7 et L8C7: P(2L3C7) => contradiction P(9L3C7).P(367L8C7) => solution avec le 6 et contradictions avec le 3 et le 7.

De Claude Renault
(Publié le 07/10/2018)

TB : 3 (6L2C8, 8L5C9, 1L6C3 ; je n'ai pas réussi à en trouver 4) 49L5C2 invalide L5C2 : le 6 couvre la grille ; le 5 est invalide

De Robert Mauriès
(Publié le 08/10/2018)

@ Claude Renault : Bonjour Claude. Vous oubliez le 6L3C1 unique dans B1. Par ailleurs, selon moi, l'invalidité de P(5L5C2) nécessite pour être démontrée l'utilisation d'une extension (bifurcation).


Ajouter un commentaire

Adresse Mail

Mot secret (Mot secret oublié)
Celui utilisé pour archiver, ou si vous n'avez jamais archivé, un mot secret de votre choix
Prénom et/ou Nom

Pour la sécurité du site,
merci de saisir les lettres et chiffres situés dans ce code : 4#+C6X59//

Commentaire


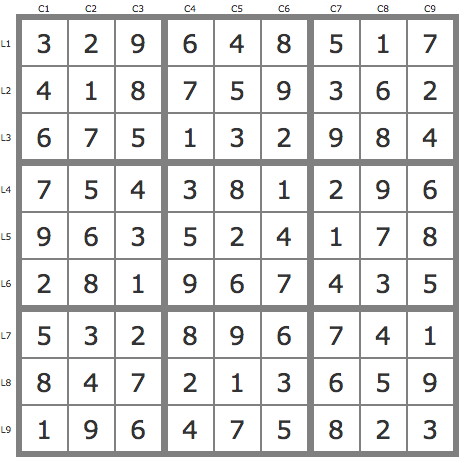
La solution

Après réduction de la grille par les TB (4 placements), on utilise le jeu de pistes JP(6L7) ou JP(6C7) : - P(6L7C6) couvre la grille. - P(6L7C7) ne compte qu'un candidat identifié, on développe donc la piste par des extensions pour constater qu'elles conduisent toutes à contradiction : - P(6L7C7).P(1L3C4) est invalide. - P(6L7C7).P(1L1C5).P(3B5) est invalide.



assistant-sudoku.com est la propriété de Robert Mauriès (assistant.sudoku(AT)free.fr). Toute reproduction interdite sans son autorisation.