S'identifier S'inscrire

assistant-sudoku.com

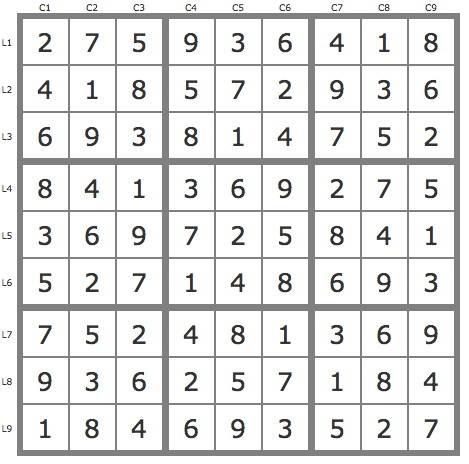
Grille Sudoku résolue

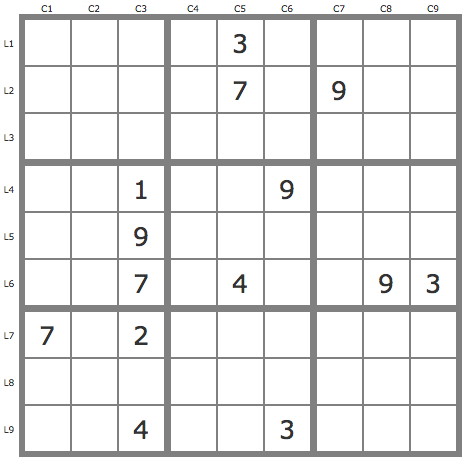
La grille -369
La technique des pistes s'applique aussi aux variantes des grilles classiques de sudoku, comme par exemple ce "sudoku non-consécutif" auquel on impose la contrainte supplémentaire suivante : deux cases voisines d'une ligne ou d'une colonne ne doivent pas avoir des chiffres qui se suivent (par exemple le 6 ne peut pas être à côté du 5 ou du 7).
Source : Sudoku Non-Consécutif - Difficile - Volume 4 - 276 Grilles, Par Nick Snels.

Afficher les commentaires Cacher les commentaires

Commentaires sur cette grille

De Robert Mauriès
(Publié le 12/06/2017)

Voir la résolution dans la rubrique "Résolutions guidées".

De Francis Labetoulle
(Publié le 13/06/2017)

Avec la règle du jeu proposées on parvient à valider 1L6C4, 6L6C7, 8L6C6, 7L8C6. La piste P1 (3L5C4) s'avère invalide donc validation de 3L4C4, 7L5C4, 2L5C5, 5L5C6, 6L4C5. 1L1C6 est impossible donc validation de 6L1C6, 1L1C6, 1L3C5... J'indique les pistes qui m'ont conduit à la solution : P2 (5L7C2) puis P21(8L7C5) et enfin P211(7L4C8). Les autres cas donnent des contradictions. Il y a probablement plus simple. Solution trouvée : 275936418418572936693814752841369275369725841527148693752481369936257184184693527. Question: la répartition obtenue, sauf erreurs, donne un cas très particulier du théorème de Tuléja avec répétition des mêmes triplets de chiffres dans lignes et colonnes d'un groupe de 3 blocs. Ce n'est probablement pas le fruit du hasard. Était-ce prévisible?

De Richard
(Publié le 13/06/2017)

Bonjour, Robert comment faites vous pour en arriver à votre grille simplifiée dans votre résolution ? Personnellement je n'arrive pas à un stade aussi avancé. Voici une image hébergée représentant la grille que j'obtiens après utilisation des TB et de la contrainte de non-consécutivité : http://nsa37.casimages.com/img/2017/06/13/170613073923282555.jpg

De JC
(Publié le 13/06/2017)

7 placements 5L4C5 -> 0 solution; L4C5=6 et fin @Robert : Même grille après l'application des règles du sudoku non-consécutif, excepté les exclusions manquantes : 5L2C3 à cause de (45)L2C4 et 5L3C5 à cause de (56)L4C5.

De JC
(Publié le 13/06/2017)

@Richard : des exclusions supplémentaires sont obtenues à partir des bilocaux, des alignements et des cases à 2 candidats. Exemples : {5B5} -> L5C5=2; {7L9} -> -(68)L9C8; (56)L4C5 -> -5L3C5; ...

De Richard
(Publié le 14/06/2017)

Bonjour, Merci JC, les choses sont plus claires maintenant. Cette contrainte de non-consécutivité pimente bien les choses en fait. Avec le 5 de L4C5 j'aboutis à une contradiction basée sur un non-respect de la nouvelle contrainte (8 en L4C8 entouré d'une paire de 7). Avec le 6 de L4C5 la grille est résolue.

Ajouter un commentaire

La solution

Après utilisation des TB et de la contrainte de non-consécutivité, la grille se simplifie pour devenir la suivante. 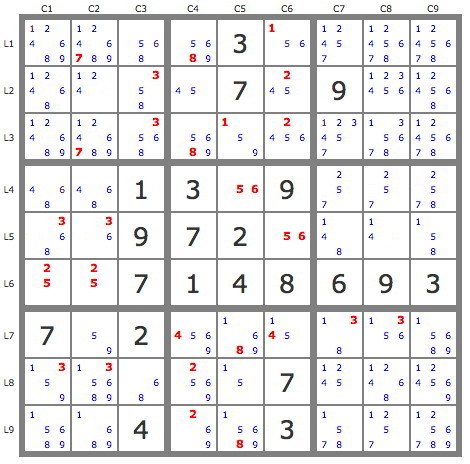Un jeu de pistes issues de la paire 1B2 permet alors par croisement des pistes (et en utilisant la contrainte de non-consécutivité) de procéder à plusieurs éliminations. 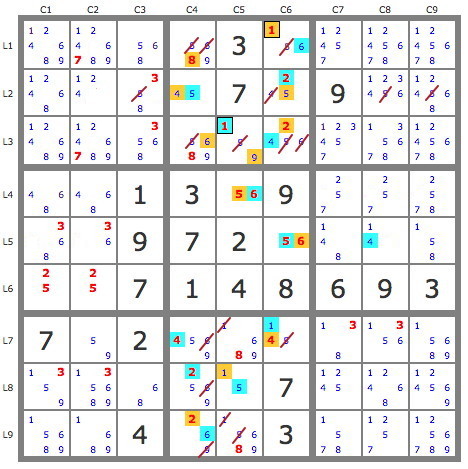En poursuivant alors, la construction de la piste jaune, on obtient quelques éliminations supplémentaires, mais surtout on débouche sur une impossibilité de satisfaire la contrainte de non-consécutivité dans L78C2, ce qui rend invalide cette piste jaune et permet de placer tous les candidats de la piste bleue. 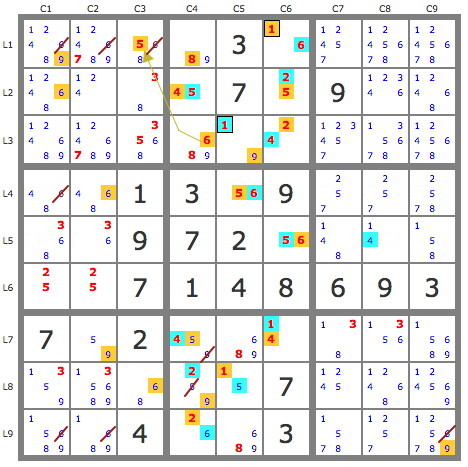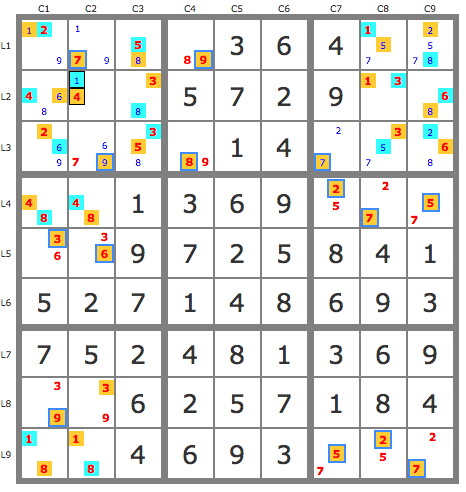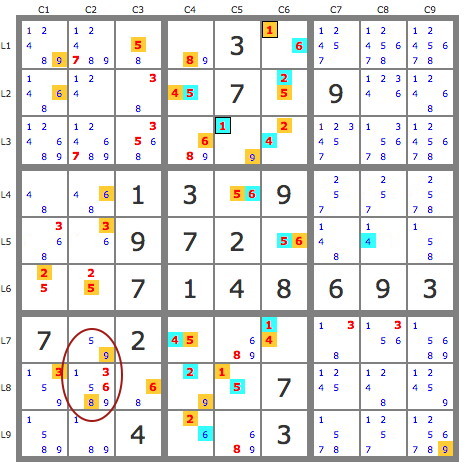Sur la grille largement simplifiée, on utilise un second jeu de pistes issue, par exemple de la paire 14L2C2. Les deux pistes se croisent suffisamment pour terminer la grille, la piste bleue couvrant la grille et la piste jaune étant invalide.