S'identifier S'inscrire

assistant-sudoku.com

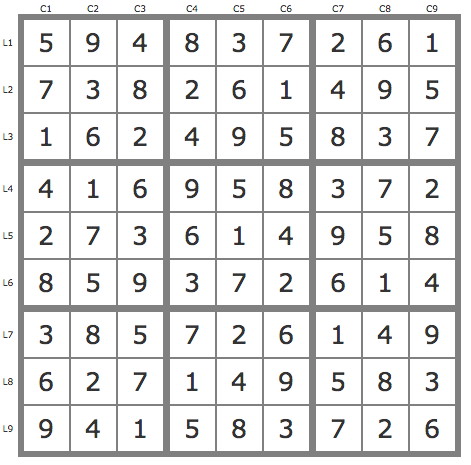
Grille Sudoku résolue

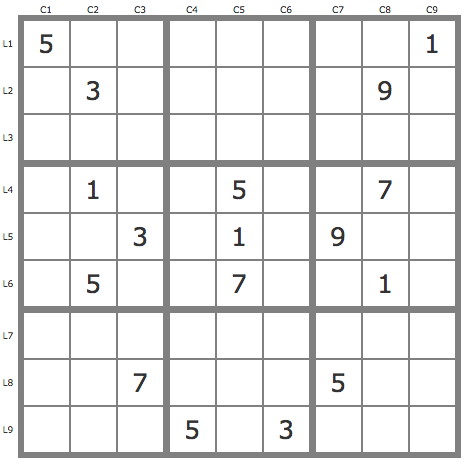
La grille -260
Cette grille est un sudoku non-consécutif, c'est à dire qu'en plus des règles habituelles s'ajoute la suivante : deux cases voisines horizontalement et verticalement ne peuvent pas contenir des chiffre consécutifs. Par exemple les cases voisines (ligne ou colonne) d'un case ayant un 6 ne peuvent pas avoir un 5 ou un 7.
La technique des pistes s'applique évidemment et un seul jeu de pistes suffit pour résoudre la grille.
( source http://sudokuvariante.blogspot.fr )

Afficher les commentaires Cacher les commentaires

Commentaires sur cette grille

De Robert Mauriès
(Publié le 06/08/2016)

Indication : paire 4B4.

De Francis Labetoulle
(Publié le 06/08/2016)

En validant 5L5C8 puis 8L5C9 ( par élimination) j'obtiens une solution à partir de l'essai 1L9C3. Les pistes issues des deux autres 1 de C3 sont invalides et la solution est donc unique! A noter que les cases contenant des paires (n,n+1) permettent des simplifications. A remarquer enfin que la solution ne présente que des triplets au sens du théorème de Tuléja.

De JC
(Publié le 06/08/2016)

L7C3=5 2L5C9 : 0 solution 4 placements HP(89-23)L4C46 6 placements HP(24-189)L13C3 L2C3≠1 sinon L1C3=L3C3=4! 9 placements Alignement(8B3)-8L9C7 4 placements L8C5≠6 sinon L7C5=4, L2C5=2 et 3B2={} L7C6=6 et fin

De Francis Labetoulle
(Publié le 08/08/2016)

Avec les 4 du bloc 4 on parvient plus vite au résultat : P1 (4L5C1) invalide puis P2 (4L4C1) , P21(8L2C3) solution et P22 (1L2C3) invalide. Donc unicité et niveau TDP au plus égal à 2 '

De Robert Mauriès
(Publié le 09/08/2016)

@ Francis Labetoulle : Le seul jeu de pistes issues de la paire 4B4 suffit à résoudre la grille qui est donc de niveau 1 TDP (Voir la résolution que je donne en détail).

De Fred Stalder
(Publié le 09/08/2016)

Bonjour, Je n'ai pas encore étudié la technique des pistes exposée sur ce site. Je peux néanmoins vous affirmer que cette technique n'est pas nécessaire pour résoudre cette variante. En effet, si on étudie la première grille de la solution, on voit que la case L8C2 contient les candidates 2 et 4, ce qui permet d'éliminer le 3 de L8C1, et donc on peut placer 3L7C1, puis 8L7C2, 2L8C2, 4L9C2, etc... Il est rare de devoir utiliser des techniques classiques avancées sur les variantes, en général une bonne connaissance des techniques liées aux règles additionnelles suffit. Fred P.S. Je suis l'auteur de ce sudoku

De Robert Mauriès
(Publié le 10/08/2016)

@ Fred Stalder : Bienvenue sur ce forum M. Stalder et merci pour votre expertise. En effet, seules les techniques de base et la propriété de non-consécutivité sont nécessaires pour résoudre cette grille. JC (sur ce forum) l'a résolue ainsi d'ailleurs. Mais c'était l'occasion de montrer que la technique des pistes s'applique à ce type de grille. Il est vrai aussi que je n'ai pas trouvé de grilles non-consécutives nécessitant obligatoirement cette technique de réseaux.

Ajouter un commentaire

La solution

Voici l'état de la grille après utilisation des techniques de base et de la règle supplémentaire des grilles non-consécutives. 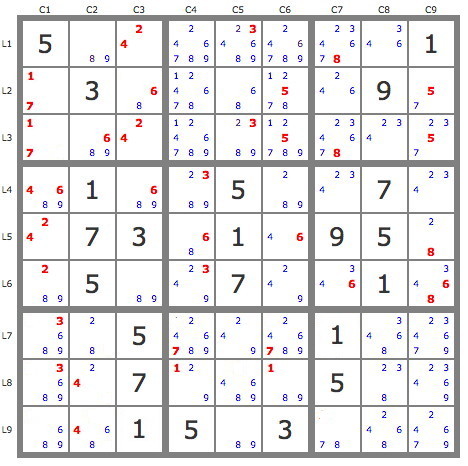Un jeu de pistes issues de la paire 4B1 permet de valider tous les candidats de la piste bleue, puisque la piste jaune rencontre une impossibilité dans L8C2 qui ne peut avoir de candidat jaune. 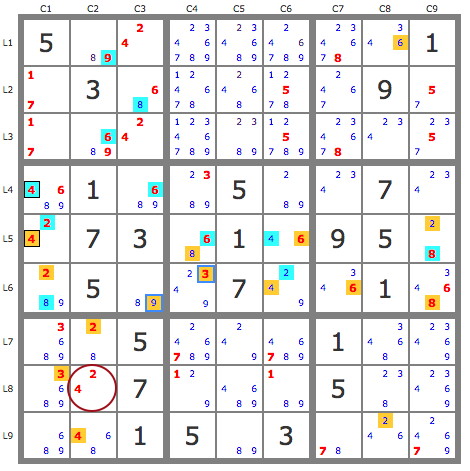Dès lors la grille se simplfie considérablement, en utilisant les techniques de base et la condition de non-consécutivité, jusqu'à devenir la suivante sur laquelle la condition de non-consécutivité permet d'éliminer le 9L3C4. 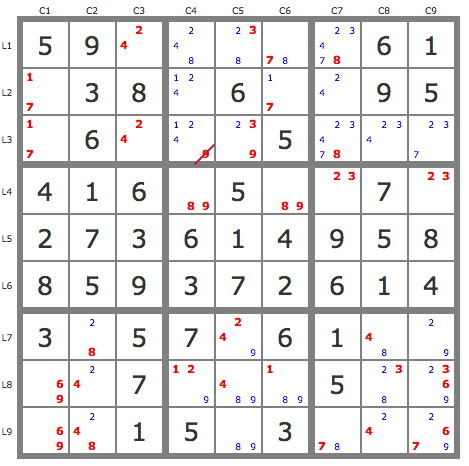Cela suffit pour résoudre la grille par les techniques de base et la condition de non-consécutivité.