S'identifier S'inscrire
assistant-sudoku.com
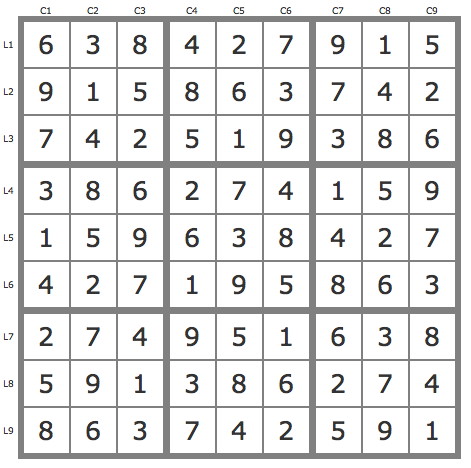
Grille Sudoku résolue
La grille -19Pour changer un peu, voici un grille sudoku non-consécutif, c'est à dire où en plus des règles habituelles du sudoku classique, on impose que deux cases voisines d'une même ligne ou d'une même colonne ne puissent pas avoir des candidats solutions consécutifs.
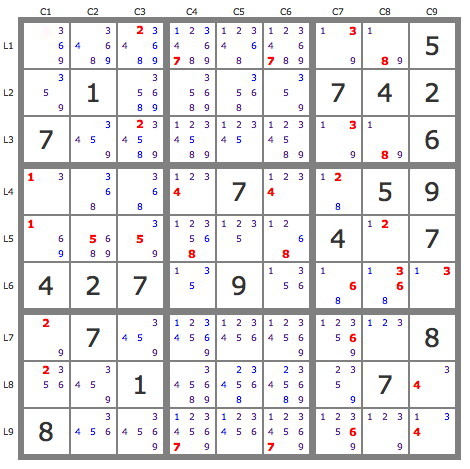
Commentaires sur cette grille
Aucun commentaire sur cette grille actuellement
Ajouter un commentaire
La solution
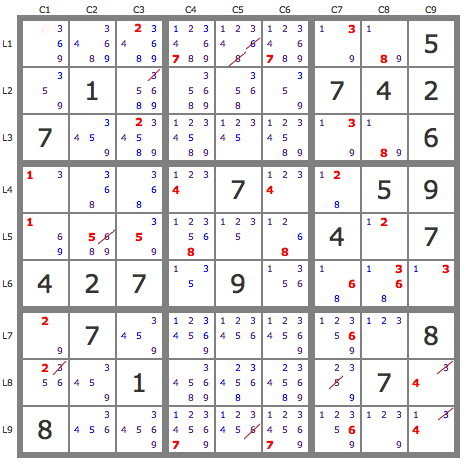
Dans un premier temps, on supprime les candidats ne pouvant pas être solution et que nous avons laissé sur la grille pour comprendre le principe du sudoku non-consécutif. Ce sont les candidats barrés d'un trait rouge. Ainsi par exemple, le 3 peut être supprimé des cases L8C9 et L9C9. En effet, si le 4 est solution de L8C9, le 3 n'est pas solution de cette case et ne peut pas l'être de la case L9C9 qui est juste dessous en raison de la règle imposée. Même raisonnement si le 4 est solution de L9C9.
La grille se simplifie encore significativement et l'on peut ensuite appliquer la technique des pistes
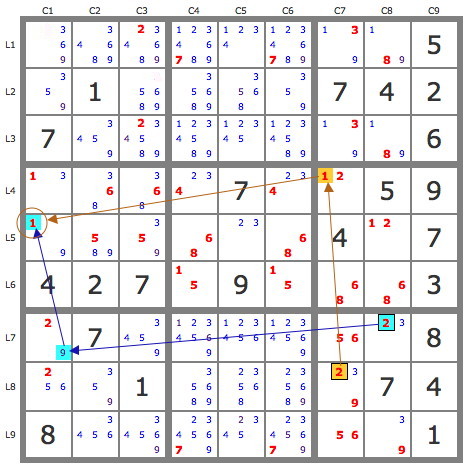
 Les pistes au départ de la paire de 2 du bloc 9 convergent vers le 1 de L5C1 qui est donc solution de cette case et en suivant cela solutionne quelques autres cases.
Les pistes au départ de la paire de 2 du bloc 9 convergent vers le 1 de L5C1 qui est donc solution de cette case et en suivant cela solutionne quelques autres cases.
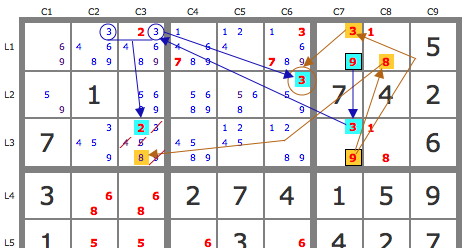
 Le jeu de pistes au départ de la paire de 9 du bloc 3 permet l'élimination de 4 candidats de la case L3C3. On voit ici comment on utilise dans la construction des pistes la condition selon laquelle deux cases ne peuvent pas avoir de solutions consécutives en ligne ou en colonne.
Au passage on détermine la solution de la case L2C6 assez évidente (X-Wing sur les 3).
Le jeu de pistes au départ de la paire de 9 du bloc 3 permet l'élimination de 4 candidats de la case L3C3. On voit ici comment on utilise dans la construction des pistes la condition selon laquelle deux cases ne peuvent pas avoir de solutions consécutives en ligne ou en colonne.
Au passage on détermine la solution de la case L2C6 assez évidente (X-Wing sur les 3).
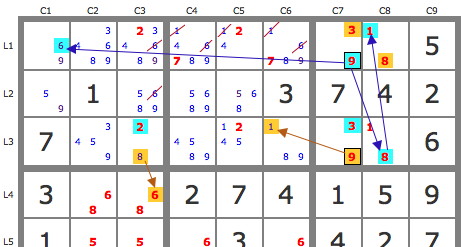
 En poursuivant le développement des deux pistes on procède encore à plusieurs éliminations (candidats barrés d'un trait rouge), ce qui conduit à trouver que le 8 est solution de la case L3C8.
La grille est résolue alors par simple induction et en tenant compte, évidemment, de la condition supplémentaire imposée aux grilles non-consécutives.
En poursuivant le développement des deux pistes on procède encore à plusieurs éliminations (candidats barrés d'un trait rouge), ce qui conduit à trouver que le 8 est solution de la case L3C8.
La grille est résolue alors par simple induction et en tenant compte, évidemment, de la condition supplémentaire imposée aux grilles non-consécutives.
 En savoir plus ...
En savoir plus ...




