
S'identifier S'inscrire
assistant-sudoku.com
Grille Sudoku résolue
La grille -496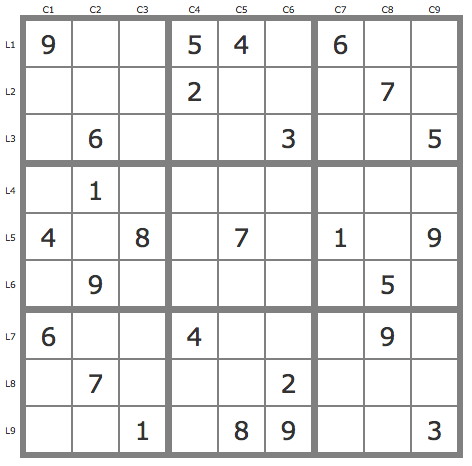
Commentaires sur cette grille
De Robert Mauriès
(Publié le 09/05/2018)
Deux placements avec les TB. - JP(7B2), avec P(7L3C4) invalide, permet de placer le 7L1C6 et 2 autres candidats. - JP(9B3) conduit à la solution avec P(9L3C7) qui couvre la grille, tandis que P(9L2C7) invalide assure l'unicité.
De Paolo
(Publié le 09/05/2018)
Bonjour, 1) 2 placements par les TB iniziales. P(3L5C8)=>couvre la grille 2)P(2L5C8)=>contradiction(L7C3= Ø via la paire 48 in B3)=>-2L5C8 3)P(6L5C8)=> contradiction (deux 9 in B3)=>validation P(3L5C8)=>solution.
De Francis Labetoulle
(Publié le 09/05/2018)
Bonjour Une première approche différente: Avec les 6 de L9 P(6L9C4) invalide donc validation de P(6L9C8). Nouvelles pistes issues de la case L5C4 : P(3L5C4) invalide et solution avec P(6L5C4) via un JC-wing des 2 de L5 validant 4L3C8. Ne me demandez surtout pas ce qu'est un JC-wing, je vous répondrais de consulter un grand nombre de commentaires antérieurs.
De Robert Mauriès
(Publié le 09/05/2018)
@ Francis Labetoulle : Beau clin d'Oeil à JC (Jean-Claude Van Hay) dont on a plus de nouvelles depuis pas mal de temps maintenant.
De Francis Labetoulle
(Publié le 09/05/2018)
Avec le même début, j'aurais pu éviter ce JC-wing en utilisant la case L5C8, (3L5C8) couvrant la grille, alors que (2L5C8) est invalide grâce à la présence des paires (48) dans B3, mais cette case a été utilisée par Paolo. Les méthodes diffèrent néanmoins. Toujours en commençant par les 6 de L9 j'aurais pu utiliser les 8 de B7, P(6L9C8).P(8L7C2) étant invalide, tandis que P(6L9C8).P(8L8C1) couvre la grille via un autre JC-wing des 2 de L5 éliminant 2L3C8.
De Robert Mauriès
(Publié le 09/05/2018)
@ Francis Labetoulle : Pour faire dans l'originalité, on peut aussi construire la solution en utilisant exclusivement les 2 de la grille avec des jeux de pistes successifs. - JP(2L5) : P(2L5C8) invalide -> placement du 2L5C2 et un autre candidat. - JP(2B7) : P(2L9C1) invalide -> placement du 2L7C3 et 8 autres candidats. - JP(2B9) : P(2L9C8) invalide -> placement du 2L9C7 et solution.
De François C.
(Publié le 10/05/2018)
@ Robert Mauriès : Bonjour, En cherchant des résolutions de taille minimale j’ai observé dans plusieurs grilles deux propriétés, dont certains d’entre vous se sont peut-être déjà rendu compte. Pour être clair j’aurai besoin des définitions suivantes (dont les deux premières ne sont pas nouvelles) : 1) Une entité est un ensemble formé de tous les candidats d’une même case, ou de tous les candidats de même valeur d’une même zone (ligne, colonne ou bloc). (Voir Théorie des pistes). 2) Un candidat (ou un ensemble) est dit « backdoor » lorsque la piste issue de ce candidat (ou de cet ensemble) conduit à une solution par simple application des techniques de base (TB). 3) Un candidat (ou un ensemble) est dit « anti-backdoor » lorsque la piste issue de ce candidat (ou de cet ensemble) conduit à une contradiction par simple application des techniques de base (TB). Les 2 propriétés suivantes concernent les grilles à solution unique: Propriété 1 : si E est un ensemble anti-backdoor inclus dans une entité, alors tous les candidats de E sont des anti-backdoors. Propriété 2 : si E est un ensemble backdoor inclus dans une entité, alors un candidat de E est un backdoor et tous les autres candidats de E sont des anti-backdoors. Remarque 1 : j’ai constaté ces propriétés en considérant les pistes P(E) comme anti-pistes issues du complémentaire de E dans l’unité (et non comme la définition de P(E) donnée dans la Théorie des pistes). Remarque 2 : les réciproques de ces 2 propriétés sont fausses. Exemple sur cette grille dans la case L5C8 : le 3 est un backdoor , le 2 et le 6 sont des anti-backdoors. Mais l’ensemble {2,6} n’est pas un anti-backdoor, et les ensembles {3,2}et {3,6} ne sont pas des backdoors. Donc cette case ne donne pas de résolution de taille 1, d’où la résolution proposée par Paolo. Remarque 3 : si la propriété 1 peut se justifier assez facilement, la propriété 2 est plus étonnante et pourtant je l’ai vérifiée plusieurs fois à l’aide d’un petit programme. A moins que ça ne soit finalement q'une lapalissade ?
De Richard
(Publié le 10/05/2018)
Bonjour, @François : effectivement vous avez parfaitement raison, j'avais déjà remarqué ceci. En faisant les grilles de Bernard Borrelly j'avais vu que lorsqu'un groupe générique aboutissait à la résolution de la grille alors l'un des candidats de ce groupe était forcément un backdoor etc... Dans mon langage personnel j'utilise le terme de "contradicteur" qui correspond à votre "anti-backdoor".
De Paolo
(Publié le 10/05/2018)
@ François Cordoliani: Bonsoir, Je crois que les deux propriétés que vous voulez relier à une grille de solution unique sont également valables pour ceux avec des solutions multiples. En ce qui concerne la propriété 2 lorsque la piste d'un ensemble E inclus dans une entite 'couvre la grille, cela signifie que la piste (E) qui est un sous-ensemble de toutes les pistes des candidats individuels de E est une backdoor et est claire qui doit être égale à seule une des pistes d'un candidat appartenant à E créerait autrement une contradiction en utilisant les TB si elle n'était pas unique. De plus, toutes les autres pistes des autres candidats de E doivent être invalides car en plus du sous-ensemble qui couvre la grille les pistes doivent nécessairement contenir au moins un élément de plus, que par force de choses, ne pas pouvoir couvrir la grille doit conduire à une invalidité.
De Robert Mauriès
(Publié le 10/05/2018)
@ François Cordoliani, Paolo et Richard : Les propriétés énoncées par François sont, me semble-t-il, des cas particulier des théorèmes suivants applicables à des grilles multi-solutions ou à solution unique et à des ensembles quelconques : - P(E) est invalide <=> P(A) est invalide pour tout candidat A de E. - P(E) est valide <=> P(A) est valide pour un candidat A de E au moins. Dans le cas d'un ensemble E qui est un sous-ensemble d'une entité, la seconde assertion se réduit à : - P(E) est valide <=> P(A) est valide pour un seul candidat A de E. La démonstration de ces deux théorèmes, comme vous le savez François de par nos échanges extra-forum, est en cours et nécessite l'élaboration de propriétés précisant la structure des pistes invalides, mais ce sont des résultats que j'ai toujours constaté empiriquement. Toutefois, ma remarque n'enlève rien à l'intérêt des remarques et propriétés énoncées par François sur les backdoors et anti-backdoors.
De François C.
(Publié le 11/05/2018)
@ Robert Mauriès : Bonjour, les théorèmes que vous citez ne permettent pas, à mon avis, de justifier les 2 propriétés que j’ai données plus haut car, dans votre théorie, une piste n’est pas considérée comme développée avec les seules techniques de base (TB). Or cela est fondamental dans la définition d’un backdoor ou d’un anti-backdoor. En détail : 1) La propriété bien connue qui dit que « P(E ) invalide => tous les candidats de E sont invalides » n’implique pas ma propriété 1. En effet un candidat invalide n’est pas forcément un anti-backdoor car la piste issue de ce candidat (donc développée avec les seules TB, j'insiste !) peut très bien ne pas aboutir à une contradiction. 2) Pour la même raison dire que « P(E) valide ==> E contient un seul candidat valide ==> tous les autres candidats de E sont invalides » n’implique pas que tous ces autres candidats soient des anti-backdoors (ce que dit ma propriété 2) . Donc, à mon avis le problème de la justification de ces 2 propriétés reste ouvert à moins que quelqu'un ne trouve des contre-exemples.
De François C.
(Publié le 11/05/2018)
@ Paolo : Bonjour, regardez le message que j'ai envoyé à Robert Mauriès, je crois que vous confondez aussi "invalide" et "anti-backdoor" et peut-être aussi "valide" et "backdoor".
De Paolo
(Publié le 11/05/2018)
@ François Cordoliani: Bonjour, Je suis entièrement d'accord avec votre définition de Backdoor. J'ai simplement dit que dans un schéma la présence d'une piste P (E), dans lequel E est un ensemble inclus dans une entité, qui résout le puzzle avec l'utilisation des TB uniquement, implique mathématiquement qu'il existe dans l'ensemble E une seule backdoor générée par un candidat de E, même si le système est à solution multiple et que tous les autres –candidates de E génèrent des pistes individuellement invalides dont la preuve d'invalidité peut être démontrée avec les TB. Si ce n'était pas le cas, cela signifierait que P (E) backdoor qui est un sous-ensemble de tout P (Ak) où Ak ∈ E génère plus d'une solution qui contredit le fait que par définition la backdoor de P (E) est unique.
De Francis Labetoulle
(Publié le 11/05/2018)
@ François Cordoliani : Bonjour Je découvre l'intéressant sujet que vous avez abordé sur le forum. Avec les hypothèses que vous avez mentionnées, et la définition actuelle de P(E), ne peut-on pas reformuler le problème mentionné ainsi : dans le cas d'un "backdoor d'ordre 1" P(E) peut-il passer par un candidat a appartenant au complémentaire de E dans l'entité? si non la propriété 2 devient-elle une évidence? Dans le premier cas toutes les pistes issues des candidats de E seraient invalides mais leur intersection serait la solution! Je n'ai pas bien saisi l'intérêt pratique de la propriété 2? Pour la nomenclature ce serait vraiment justifié de trouver des expressions plus simples...
De François C.
(Publié le 11/05/2018)
@ Paolo : Vous dites que P(E) est inclus dans chaque P(Ak) ce qui suppose que vous supposez que P(E) est l’intersection des P(Ak), ce qui en effet est la définition de P(E ) dans la théorie des pistes. Bien, seulement voilà, il y a un petit problème: j’ai bien précisé, après l’énoncé de mes propriétés, que je considérais une piste P(E) comme l’anti-piste du complémentaire de E dans l’unité concernée, et non pas comme l’intersection des P(Ai) où les Ai sont les candidats de E. (C’est d’ailleurs ce que tout le monde fait sur le forum dans la course à la résolution de taille minimale. Faire l’intersection de plusieurs pistes serait fastidieux et coûterait trop cher de ce point de vue). Si le théorème 2-1 de la théorie des pistes nous dit que les deux pistes obtenues (soit par l'anti-piste, soit par l'intersection de pistes) sont équivalentes, il faut quand même savoir que ça ne marche pas si le développement des pistes se fait uniquement avec les techniques de bases. J’en ai discuté avec Robert Mauriès (hors forum) et nous sommes d’accord sur ce point. Donc pour le cas qui nous concerne, considérer l’anti-piste ou l’intersection des pistes ne revient pas au même puisque justement je prends comme hypothèse qu’on n’utilise que les techniques de base pour développer les pistes. J’espère que vous me suivez…
De François C.
(Publié le 11/05/2018)
@ Francis Labetoulle : Bonsoir, Vous dites "P(E) peut-il passer par un candidat appartenant au complémentaire de E dans l'entité?" Je crois qu'il faut plutôt se poser la question: « P(E) passe-t-il par un candidat de E? » Si la réponse était oui, on aurait prouvé la moitié de la propriété 2, à savoir que si E est un backdoor, alors un candidat de E est un backdoor. Mais cela ne démontrerait pas toute la propriété. Ensuite vous dites : "Dans le premier cas toutes les pistes issues des candidats de E seraient invalides mais leur intersection serait la solution! » Je suppose que par "premier cas" vous entendez la propriété 1. Donc supposons que P(E) est un anti-backdoor. Si on pouvait affirmer que P(E) passe par un candidat de E, alors on pourrait conclure que ce candidat est un anti-backdoor, donc finalement qu’un candidat de E est anti-backdoor. Rien de plus. Enfin pour ce qui de l’intérêt de ces propriétés, il réside dans la recherche de résolutions de taille minimales. Prenons un exemple : Dans cette grille 496, après exécution des techniques de base, la case L1C8 contient 4 candidats : le 2 (backdoor), le 8 (anti-backdoor) , et le 1 et le 3 dont on ne peut rien dire. Si je cherche une résolution de taille 1 à partir de cette case, je vais chercher 2 sous-ensembles complémentaires par exemple E1 = {1,2} et E2 = {3,8}, E1 étant susceptible d’être backdoor (BD) et E2 d’être anti-backdoor (ABD). Et bien la propriété 1 me dit que E2 ne peut pas être ABD car le 3 n’est pas ABD, et la propriété 2 me dit que E1 ne peut pas être BD car le 1 n’est pas ABD. Donc économie d’essais.
De Paolo
(Publié le 11/05/2018)
@ François Cordoliani : Bonsoir, Je reproduis exactement ce que vous avez déclaré dans votre message sur théorème 2-1: Si le théorème 2-1 de la théorie des pistes nous dit que les deux pistes obtenues (soit par l'anti-piste, soit par l'intersection de pistes) sont équivalentes, il faut quand même savoir que ça ne marche pas si le développement des pistes se fait uniquement avec les techniques de bases. Je suis clairement d'accord sur la première partie de ce que vous avez écrit: le théorème 2-1 de la théorie des pistes nous dit que les deux pistes obtenues (soit par l'anti-piste, soit par l'intersection de pistes) sont équivalentes, Alors que sur la deuxième partie: il faut quand même savoir que ça ne marche pas si le développement des pistes se fait uniquement avec les techniques de bases. Je semble saisir une contradiction telle qu'écrite. En fait c'est possible même si c'est beaucoup plus difficile, puisqu'ils sont équivalents, développement des pistes avec les techniques de bases. En effet, il suffit de développer, en utilisant uniquement la technique de base, toutes les pistes P (Ak) et d'identifier les composantes communes = B (le sous-ensemble) dont la piste P (B) est exactement équivalente à P (E). Je sais que personne n'utilise cette méthode car il est beaucoup plus facile de développer le même P (E) en utilisant P '(E1) où E1 est complémentaire de E, mais cela est utile pour démontrer la propriété 2 de votre post précédent: Propriété 2 : si E est un ensemble backdoor inclus dans une entité, alors un candidat de E est un backdoor et tous les autres candidats de E sont des anti-backdoors. 1) Le backdoor P (B) ou P (E) est unique et comprend parmi ses candidats seulement l'un des –Ak de E 2) Tous les autres pistes P (Ak) peut être généré à partir des éléments de B plus le seul Ak qui est déterminante pour l'invalidité telle qu'elle est, dans l'entité, différent de celui présent dans backdoor. Exemple sur la grille 496 en cours: E = {L1C8 = 2; L3C8 = 2; L4C8 = 2} et E1 = {L5C8 = 2; L9C8=2} P (E) = P '(E1) => couvre la grille; P (2L1C8) => couvre la grille B = croisement des pistes P (2L1C8), P (2L3C8) et P (2L4C8) = {P(2L5C2).P(6 L9C8)} P (B)=P(2L5C2).P(6L9C8) => couvre la grille. P (2L3C8) => invalide et P (2L4C8) => invalide en utilisant le TB P(B+Ak)=P(2L5C2).P(6L9C8).P(2L1C8)=> couvre la grille P(B+Ak)=P(2L5C2).P(6L9C8).P(2L3C8)=> invalide en utilisant le TB P(B+Ak)=P(2L5C2).P(6L9C8).P(2L4C8)=> invalide en utilisant le TB
De Robert Mauriès
(Publié le 12/05/2018)
@ Paolo, François et Francis : Bonjour, E1 et E2 formant une paire d'ensemble, François a raison de dire que l'équivalence P(E1)=P'(E2), où P(E1) est obtenue par intersection de ses composantes, n'est pas vraie pour les traces de P(E1) et P'(E2), c'est à dire si on n'utilise que les TB pour développer P(E1) et P'(E2) (voir définition d'une trace dans Théorie des pistes). On peut construire des contre-exemples qui le prouvent. Cette équivalence est vraie pour les pistes et non pour leurs traces . Ceci dit, la piste P(E1) obtenue selon François en développant la trace de P'(E2) ne peut se faire que si on est en mesure de développer P(E1) par intersection de ses composantes. Ce qui revient à dire que les deux définitions de P(E) sont équivalentes dans le cas d'un tel ensemble E. Dans la pratique que vous évoquez François, on choisit toujours E1 de manière à exploiter un doublet (ou un triplet) caché, ce qui assure que l'intersection des composantes fonctionne. Dès lors, pour les propriétés énoncées par François, les démonstrations sont les suivantes, en notant _P la trace de P : 1) Si _P(E) est invalide (anti-backdoor) => _P(A) est invalide (anti-backdoor) pour tout A appartenant à E, car si les candidats de _P(E) font apparaître une contradiction ceux de _P(A) aussi puisque _P(E) est un sous-ensemble de _P(A). J'insister sur le fait que si on est en mesure de construire _P(E) c'est qu'on est en mesure de construire _P(A). 2) Si _P(E) couvre la grille (backdoor), il existe S1 telle que _P(E)=S1 => pour tout Ak appartenant à E, _P(Ak) contient tous les candidats de S1. D'après le théorème que j'évoquais dans un précédent commentaire, à savoir "P(E) valide <=> P(A) valide pour un A appartenant à E", je peux dire que pour un A de E _P(A)=S1 (backdoor). Pour tous les autres candidat Ak de E _P(Ak) est S1-invalide (S1-anti-backdoor) puisque dans la case de Ak cette piste contient deux candidats Ak et A. Si, comme le suppose François, la grille est à solution unique, le S1-anti-backdoor est un anti-backdoor. Bien amicalement à vous trois qui animez le forum si régulièrement.
De Paolo
(Publié le 12/05/2018)
@ Robert Mauriès: Bonjour, Désolé, mais j'aimerais mieux comprendre. Je cite la définition de P (E) et l'énoncé du théorème 2-1: 3) Une piste P(E) issue d’un ensemble de candidats E est l’ensemble des candidats Ai ∈ G communs à toutes les pistes issues de tous les candidats Ak ∈ E . On a donc P(E) =∩E P(Ak), soit P(E) ⊆ P(Ak) ∀k. et Théorème 2-1 : Si E1 et E2 forment une paire d’ensembles, la piste P(E1) issue de E1 et identique à l’antipiste P’(E2) issue de E2, et réciproquement. En particulier, si deux candidats forment une paire, la piste issue de l’un et identique à l’antipiste issue de l’autre. A partir de la première définition de P (E), je comprends que E1 et E2 du Théorème 2-1 doivent également être inclus dans cette définition. Alors P (E1) =∩E P(Ak), soit P(E1) ⊆ P(Ak) ∀k et P (E2) = ∩E2 P (Ak), soit P (E2) ⊆ P (Ak) ∀k. De cette conclusion je demande pourquoi il n'est pas possible "théoriquement", même si c'est très difficile, de développer les pistes P (E1) et P (E2) en utilisant la définition de P (E) et la technique de base décrite dans mon article précédent ?
De Francis Labetoulle
(Publié le 12/05/2018)
Bonjour à tous Je dois et vais approfondir les commentaires de chacun. Néanmoins je n'ai pas lu de réponse aux questions que je me posais. Oublions la définition actuelle de P(E) et adoptons celle de l'antipiste du complémentaire : ensemble des candidats que l'on placerait avec les TB ici , si on éliminait tous les candidats de ce complémentaire de E dans l'entité. Dans le cas où ce P(E) donne la solution, il me semble que celle-ci contient donc un candidat (disons a) de E. Les pistes issues d'autre(s) candidats de E sont donc invalides et la propriété 2 est vérifiée? Pour autant à quoi sert-elle pratiquement? C'est P(E) qui donne un résultat "riche" quant au calcul de la taille. Maintenant peut-on affirmer la même chose avec la définition actuelle de P(E)? Tout cela est-il trivial ou non ?
De Paolo
(Publié le 12/05/2018)
@ Robert Mauriès: Bonjour, Désolé, mais je n'ai pas lu la deuxième partie du message qui est complètement d'accord avec ce que j'ai écrit dans le post précédent. Je voudrais ajouter seulement au point 2 que l'hypothèse de François, la grille est à solution unique, n'est pas nécessaire puisque P (E) étant un Backdoor est unique dans l'ensemble E.
De Robert Mauriès
(Publié le 12/05/2018)
@ Francis Labetoulle : La réponse à votre question Francis est OUI, ceci en vertu des théorèmes suivants dont je travaille, comme vous les savez, à la démonstration : "P(E)=∩P(Ai) invalide <=> P(Ai) invalide quel que soit Ai appartenant à E" et sa contraposée, " P(E)=∩P(Ai) valide <=> P(Ai) valide pour un candidat Ai au moins appartenant à E", ceci pour tout ensemble E=∪Ei dont les contre-composantes Ei' (complémentaire de Ei dans la case de Ei) ne sont pas vides, donc en particulier pour un ensemble faisant partie d'une paire d'ensemble.
De Paolo
(Publié le 12/05/2018)
@ Robert Mauriès: Bonjour, Je voudrais vous présenter un problème sur la définition de la taille qui découle de la discussion que nous avons entreprise sur la grile actuelle. Lorsque nous avons une case avec seulement deux candidats présents dont un est une backdoor et l’autre que génère une piste invalide, nous pouvons généralement avoir deux solutions de taille 1, Une en raison de la contradiction générée par le candidat différent de backdoor de taille 1 et l’autre à partir de l'intersection des deux pistes presente. Cette solution, comme discuté dans le forum, peut être interprétée comme l'extension d'une paire d' ensemble entre la piste P (E) et P (E1) en où E est l'ensemble des deux candidats et E1 = Ø, l'ensemble vide. Dans ce cas la piste P (E) s'il y a une solution pour croisement de deux pistes peut être interprétée comme une nouvelle backdoor par analogie à quand E est formé par au moins deux candidats et E1 n'est pas vide. De cette façon, il y aurait une différence entre la solution de croisement et la solution d'invalidité de l'une des deux pistes. Il me semble que dans certains cas ces deux solutions ne se produisent pas simultanément. La solution pour croisement de deux pistes implique toujours une backdoor et une piste invalide alors qu'une piste invalide et une backdoor n'impliquent pas toujours une solution par croisement des pistes.
De François C.
(Publié le 12/05/2018)
@ Robert Mauriès : Bonjour, je pense que votre idée est la bonne, en tous cas je ne vois pas d’autre façon de faire pour justifier la propriété 2 en tous cas. Cependant tout ne coule pas de source car vous admettez certains points qui ne sont qu’en cours de démonstration, si j’ai bien compris. Il s’agit de : 1) la réciproque de la propriété 3-6 a) de la théorie des pistes, à savoir : "P(E) est une solution => il existe un candidat de E qui appartient à cette solution". 2) Si E1 et E2 forment une paire d’ensembles alors _P’(E2) est inclus dans _P(E1), donc dans l’intersection des _P(Ak), donc finalement dans chaque _P(Ak). (Les Ak étant les candidats de E1). Il s’agit donc d’une partie du théorème 2-1 mais concernant les pistes limitées à leur trace et c’est là qu’est toute la subtilité. Et sur ce point je ne suis pas très convaincu par votre " .. on choisit toujours E1 de manière à exploiter un doublet (ou un triplet) caché, ce qui assure que l'intersection des composantes fonctionne." qui semble restreindre la démonstration à des cas le plus souvent pratiqués… même si je comprends bien ce que vous voulez dire. En tous cas ce petit problème me fait mieux comprendre l’intérêt des intersections de pistes et du développement des pistes invalides qui se cache derrière tout ça (je ne vais pas détailler plus ici) …
De Robert Mauriès
(Publié le 12/05/2018)
@ Paolo : Les deux façons de procéder que vous indiquez, sont en réalité totalement équivalentes, car il est toujours possible de prolonger la construction de la piste invalide P1 malgré ses contradictions jusqu'à ce qu'elle croise suffisamment la piste valide P2 pour que la piste P1∩P2 résultant de ce croisement couvre la grille elle aussi. Il est vrai qu'en général on arrête la construction d'une piste invalide dès qu'on rencontre une contradiction car alors on ne respecterait plus la règle R du sudoku si l'on plaçait deux candidats dans une case. Pourtant il est possible de poursuivre la construction d'une piste invalide P en respectant R partiellement, c'est-à-dire en plaçant un candidat Ao par les TB à partir de p candidats A1, A2..., Ap appartenant à P de telle manière que le placement de Ao, A1, A2 ..., Ap respecte R indépendamment des autres candidats de P. P invalide est multiforme et est la réunion de toutes les constructions possibles faites de cette manière. Conscient que la définition actuelle d'une piste ne permet pas de bien comprendre la structure d'une piste invalide, je suis en train de repenser cette définition qui sera publiée prochainement.
De François C.
(Publié le 12/05/2018)
@ Francis Labetoulle : Vous dites : "Dans le cas où ce P(E) donne la solution, il me semble que celle-ci contient donc un candidat (disons a) de E". Nous en sommes tous convaincus mais ceci reste à démontrer (c’est la réciproque de la propriété 3-6 de la théorie des pistes). Vous dites : « Les pistes issues d'autre(s) candidats de E sont donc invalides et la propriété 2 est vérifiée? « Si je suppose la grille à solution unique, les pistes en question sont bien invalides mais la propriété 2 n’est pas pour autant forcément vérifiée. En effet une piste P(A) invalide n’implique pas que A soit un anti-backdoor car l’application des techniques de base ne suffit pas toujours à faire apparaître une contradiction. Enfin concernant l’utilité de ces propriétés je vous ai donné un exemple dans un message antérieur. Voici quelques détails supplémentaires: supposez que vous ayez trouvé une résolution de taille 2 pour votre grille. La question qui va se poser est celle-ci : existe-t-il une résolution de taille 1 ? Si vous êtes très patient vous aller chercher toutes les partitions possibles de chaque entité en 2 sous-ensembles E1, E2 en espérant trouver un cas où E1 est un backdoor et E2 est un anti_backdoor. Si c’est le cas vous pourrez affirmer que la grille est de taille 1. Seulement cela peut faire beaucoup de combinaisons à tester (plusieurs centaines). Il sera alors plus rapide de commencer par déterminer si chaque candidat et un backdoor ou un anti-backdoor et d’appliquer ensuite les propriétés 1 et 2 dans chaque entité, de façon à éliminer d’emblée les combinaisons (E1, E2) qui ne conviennent pas (voir mon message antérieur). Ceci dit, même cela restera un travail de fourmi s’il est fait sans aucune aide informatique.
De François C.
(Publié le 12/05/2018)
@ Paolo : Bonsoir, je réponds à votre dernier message du 11/05. Si j’ai bien compris vous essayez de justifier la propriété 2 en considérant P(E) comme intersection des P(Ak) où les Ak sont les candidats de E. En fait cela n’a pas de sens car je viens de me rendre compte que la définition que j’ai donnée d’un ensemble backdoor n’a elle-même pas de sens ! La raison est qu’une piste sur un ensemble est définie (dans la théorie des pistes) comme intersection de pistes qui elles-mêmes ne sont pas censées être construites avec les seules techniques de base (TB). Et d'ailleurs il vaut mieux qu'elles ne le soient pas ! Car il se trouve que si vous construisez des P(Ak) avec les TB seules et que vous faites leur intersection ensuite, vous risquez avec un peu de malchance, d’obtenir quelque chose d’incorrect (par exemple une intersection de 2 pistes invalides qui ne contiendrait que des candidats valides !). Donc dire que P(E) est construite avec les seules techniques de base n’a pas de sens ou risque de conduire à une aberration. Je corrige donc mes définitions comme suit : 1) Un ensemble de candidats E1 d’une entité E est dit « backdoor » si l’anti-piste P’(E – E1) construite avec les seules techniques de base conduit à une solution. 2) Un ensemble de candidats E1 d’une entité E est dit « anti-backdoor » si l’anti-piste P’(E – E1) construite avec les seules techniques de base conduit à une contradiction. Les 2 propriétés, elles, ne changent pas et c'est bien avec les nouvelles définitions ci-dessus que je les ai testées et non pas avec les anciennes. Maintenant, bien sûr, rien ne vous empêche de rapprocher P'(E - E1) de P(E1): voir la proposition de Robert Mauriès et ma réponse correspondante. Disons que l'affaire n'est pas tout à fait réglée à mon avis mais l'idée est là, en tous cas je n'en vois pas d'autre.
De Paolo
(Publié le 13/05/2018)
@ François Cordoliani: Excusez-moi, mais je ne suis pas d'accord avec ce que vous dites dans la première partie de votre dernier message. La propriété 2 de votre message du 10/05 est correcte car elle vient directement du théorème 2-1, dont la preuve est correcte, sauf si vous voulez réécrire complètement toutes les définitions et en particulier celles des pistes d'un ensemble et par conséquent réécrire une autre théorie. Je signale une partie de votre message: Car il se trouve que si vous construisez des P(Ak) avec les TB seules et que vous faites leur intersection ensuite, vous risquez avec un peu de malchance, d’obtenir quelque chose d’incorrect (par exemple une intersection de 2 pistes invalides qui ne contiendrait que des candidats valides !). Donc dire que P(E) est construite avec les seules techniques de base n’a pas de sens ou risque de conduire à une aberration. La propriété 2 que vous avez décrite n'affecte pas tous les P (E1) mais uniquement ceux qui sont inclus dans une paire d'ensemble. Dans ce cas, il est assez facile de montrer qu'un sous-ensemble créé par tous les P (Ak), qui génèrent le P (E1), si elles étaient invalides, ne pouvait pas générer une backdoor. En fait, cela possible sous-ensemble = B ne peut pas générer une piste P (B) dans lequel est présente comme un élément une des AK, car cet élément si c'est présent serait lui-même créer un' invalidité et par conséquent ne serait pas en mesure de couvrir la grille. Il faudrait donc que P (E1) serait égal à P ‘(E1) et le backdoor éventuelle générée serait un P (Ak2) d'un Ak présent dans l'E2 complémentaire. Donc, résumant cette possible P (Ak2), backcdoor serait en mesure de générer le même sous-ensemble qui l'a généré, ce qui détermine également l'élimination de toutes les AK1. Ceci est impossible car le sous-ensemble générerait l'élimination de tous les éléments qui l'ont généré.
Ajouter un commentaire
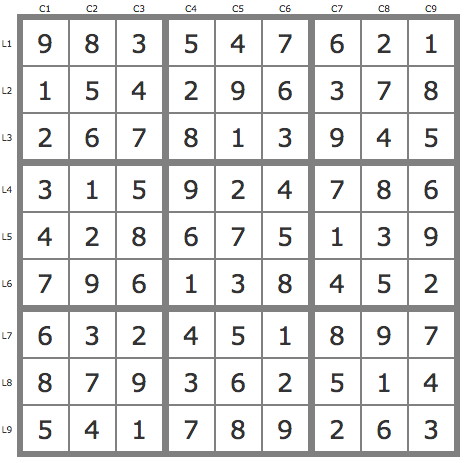
La solution
Deux placements avec les TB.
- JP(7B2), avec P(7L3C4) invalide, permet de placer le 7L1C6 et 2 autres candidats.
- JP(9B3) conduit à la solution avec P(9L3C7) qui couvre la grille, tandis que P(9L2C7) invalide assure l'unicité.
 En savoir plus ...
En savoir plus ...





