
S'identifier S'inscrire
assistant-sudoku.com
L'assistant sudoku
L'assistant sudoku vous aide à résoudre vos grilles sudoku les plus difficiles. L'assistant sudoku ne recherche pas la solution à votre place, il vous aide seulement à résoudre votre grille.En savoir plus ...
Une technique universelle de résolution
La technique des pistes permet de résoudre les grilles les plus difficiles. Cette technique intuitive évite de mémoriser les nombreuses méthodes dites "Expertes" utilisées habituellement.En savoir plus ...
Résolution guidée
Régulièrement ici une nouvelle grille et sa résolution par la technique des pistes.Toutes les grilles avec résolution guidée
Grille -712 (Publiée le 06/12/2022)
Grille proposée sur New Sudoku Player's Forum par SteveG48.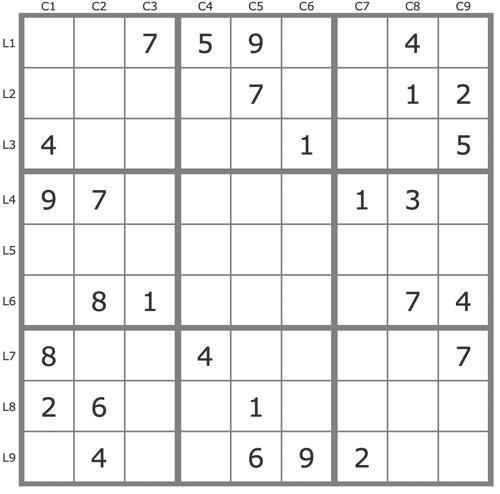
Résoudre la grille ... | Voir la résolution ... | Afficher les commentaires
Commentaires sur cette grille
De Robert Mauriès
(Publié le 06/12/2022)
Grille de niveau 1 TDP. Résolution en cliquant sur voir la résolution.
De Bruno Greco
(Publié le 06/02/2024)
Bonjour, bravo pour votre site.
Voici une variante de votre solution :
Au stade de votre diagramme, les 6 en C6 et L4 éliminent 6L1C9. En résulte 5L6C7 et 89L5C7, alors :
8L5C7->3L5C5 ou 9L5C7->9L2C2->3L3C2
éliminent 3L3C5 et termine par unicités comme vous.
Cordialement
Bruno Greco
De bordes06
(Publié le 03/03/2024)
Bonjour,
Je vous propose de découvrir un site que je viens de développer :
http://sudoku06.fr
Il permet deux choses :
1) résoudre une grille manuellement, avec éventuellement des indices proposés par l'ordinateur afin de progresser lorsque l'on est bloqué ;
2) demander à l'ordinateur de résoudre une grille pas à pas, c'est à dire comme le ferait un humain.
Il me semble que c'est un outil très utile pour progresser dans la connaissance des techniques de résolution. En complément des techniques de base, cet outil gère les techniques telles que X-WING, XY-WING, rectangle unique, chaines forcées, coloriage, Swordfish. Lorsqu'aucune de ces techniques ne permet de terminer une grille, la force brute est utilisée.
La force brute n'est jamais vraiment satisfaisante. J'aimerais développer d'autres techniques de résolution afin d'éviter cette technique. Si vous avez des idées...
Il y a trois façons de saisir une grille :
1) manuellement ;
2) par niveau de difficulté ;
3) par des grilles prédéfinies (ce qui permet de mieux comprendre les techniques compliquées).
Il est possible de sélectionner les techniques permises. Toujours dans l'idée de se familiariser avec celles-ci.
Enfin, le site est entièrement gratuit. Je n'ai rien à vendre !
Bonne journée,
Michel B.
Ajouter un commentaire
Problème de sudoku
Apprenez à manier la technique des pistes par les problèmes de sudoku.PB-38 : Piste issue d'un ensemble
En utilisant la notion de piste issue d'ensemble, montrer que le 4 et le 9 de L1C7 peuvent être éliminés. De même montrer que l'on peut éliminer les 8 de L2C124.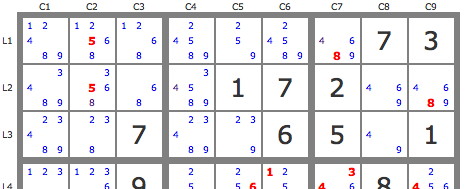
Voir la solution ...
Sudoku non-consécutif, diagonal et hyper-sudoku
L'assistant sudoku permet évidemment de traiter les grilles de sudoku non-consécutif, de sudoku-diagonal et d'hyper-sudoku.En savoir plus ...
 En savoir plus ...
En savoir plus ...





